Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1997 AIME Problems/Problem 4"

 
 
(9 intermediate revisions by 9 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
 +
[[Circle]]s of [[radii]] <math>5, 5, 8,</math> and <math>\frac mn</math> are mutually externally tangent, where <math>m</math> and <math>n</math> are relatively prime positive integers.  Find <math>m + n.</math>
  
 
== Solution ==
 
== Solution ==
 +
[[Image:1997_AIME-4.png]]
 +
 +
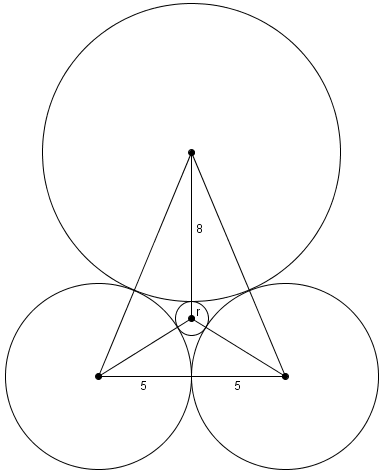
If (in the diagram above) we draw the line going through the centers of the circles with radii <math>8</math> and <math>\frac mn = r</math>, that line is the perpendicular bisector of the segment connecting the centers of the two circles with radii <math>5</math>. Then we form two [[right triangles]], of lengths <math>5, x, 5+r</math> and <math>5, 8+r+x, 13</math>, wher <math>x</math> is the distance between the center of the circle in question and the segment connecting the centers of the two circles of radii <math>5</math>. By the [[Pythagorean Theorem]], we now have two equations with two unknowns:
 +
 +
<cmath>\begin{eqnarray*}
 +
5^2 + x^2 &=& (5+r)^2 \\
 +
x &=& \sqrt{10r + r^2} \\
 +
&& \\
 +
(8 + r + \sqrt{10r+r^2})^2 + 5^2 &=& 13^2\\
 +
8 + r + \sqrt{10r+r^2} &=& 12\\
 +
\sqrt{10r+r^2}&=& 4-r\\
 +
10r+r^2 &=& 16 - 8r + r^2\\
 +
r &=& \frac{8}{9}
 +
\end{eqnarray*}</cmath>
 +
 +
So <math>m+n = \boxed{17}</math>.
 +
 +
 +
NOTE: It can be seen that there is no apparent need to use the variable x as a 5,12,13 right triangle has been formed.
 +
== Solution 2 ==
 +
We may also use Descartes' theorem, <math>k_4=k_1+k_2+k_3\pm 2\sqrt{k_1k_2+k_2k_3+k_3k_1}</math> where each of <math>k_i</math> is the curvature of a circle with radius <math>r_i</math>, and the curvature is defined as <math>k_i=\frac{1}{r_i}</math>. The larger solution for <math>k_4</math> will give the curvature of the circle externally tangent to the other circles, while the smaller solution will give the curvature for the circle internally tangent to each of the other circles. Using Descartes' theorem, we get <math>k_4=\frac15+\frac15+\frac18+2\sqrt{\frac{1}{40}+\frac{1}{40}+\frac{1}{25}}=\frac{21}{40}+2\sqrt{\frac{45}{500}}=\frac{45}{40}</math>. Thus, <math>r_4=\frac{1}{k_4}=\frac{40}{45}=\frac89</math>, and the answer is <math>\boxed{017}</math>
 +
 +
==Video Solution 1==
 +
https://www.youtube.com/watch?v=KUs44jwBLD8&t=118s
 +
-amritvignesh0719062.0
  
 
== See also ==
 
== See also ==
−
* [[1997 AIME Problems]]
+
{{AIME box|year=1997|num-b=3|num-a=5}}
 +
 
 +
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 21:33, 2 February 2021

Problem

Circles of radii $5, 5, 8,$ and $\frac mn$ are mutually externally tangent, where $m$ and $n$ are relatively prime positive integers. Find $m + n.$

Solution

1997 AIME-4.png

If (in the diagram above) we draw the line going through the centers of the circles with radii $8$ and $\frac mn = r$, that line is the perpendicular bisector of the segment connecting the centers of the two circles with radii $5$. Then we form two right triangles, of lengths $5, x, 5+r$ and $5, 8+r+x, 13$, wher $x$ is the distance between the center of the circle in question and the segment connecting the centers of the two circles of radii $5$. By the Pythagorean Theorem, we now have two equations with two unknowns:

\begin{eqnarray*} 5^2 + x^2 &=& (5+r)^2 \\ x &=& \sqrt{10r + r^2} \\ && \\ (8 + r + \sqrt{10r+r^2})^2 + 5^2 &=& 13^2\\ 8 + r + \sqrt{10r+r^2} &=& 12\\ \sqrt{10r+r^2}&=& 4-r\\ 10r+r^2 &=& 16 - 8r + r^2\\ r &=& \frac{8}{9} \end{eqnarray*}

So $m+n = \boxed{17}$.


NOTE: It can be seen that there is no apparent need to use the variable x as a 5,12,13 right triangle has been formed.

Solution 2

We may also use Descartes' theorem, $k_4=k_1+k_2+k_3\pm 2\sqrt{k_1k_2+k_2k_3+k_3k_1}$ where each of $k_i$ is the curvature of a circle with radius $r_i$, and the curvature is defined as $k_i=\frac{1}{r_i}$. The larger solution for $k_4$ will give the curvature of the circle externally tangent to the other circles, while the smaller solution will give the curvature for the circle internally tangent to each of the other circles. Using Descartes' theorem, we get $k_4=\frac15+\frac15+\frac18+2\sqrt{\frac{1}{40}+\frac{1}{40}+\frac{1}{25}}=\frac{21}{40}+2\sqrt{\frac{45}{500}}=\frac{45}{40}$. Thus, $r_4=\frac{1}{k_4}=\frac{40}{45}=\frac89$, and the answer is $\boxed{017}$

Video Solution 1

https://www.youtube.com/watch?v=KUs44jwBLD8&t=118s -amritvignesh0719062.0

See also

1997 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1997_AIME_Problems/Problem_4&oldid=144734"