Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2017 AIME I Problems/Problem 15"

m (→‎Solution 2 (No Coordinates))
m (→‎Solution 2)
 
(67 intermediate revisions by 23 users not shown)
Line 2: Line 2:
  
 
The area of the smallest equilateral triangle with one vertex on each of the sides of the right triangle with side lengths <math>2\sqrt{3},~5,</math> and <math>\sqrt{37},</math> as shown, is <math>\frac{m\sqrt{p}}{n},</math> where <math>m,~n,</math> and <math>p</math> are positive integers, <math>m</math> and <math>n</math> are relatively prime, and <math>p</math> is not divisible by the square of any prime. Find <math>m+n+p.</math>
 
The area of the smallest equilateral triangle with one vertex on each of the sides of the right triangle with side lengths <math>2\sqrt{3},~5,</math> and <math>\sqrt{37},</math> as shown, is <math>\frac{m\sqrt{p}}{n},</math> where <math>m,~n,</math> and <math>p</math> are positive integers, <math>m</math> and <math>n</math> are relatively prime, and <math>p</math> is not divisible by the square of any prime. Find <math>m+n+p.</math>
 +
 +
<asy>
 +
size(5cm);
 +
pair C=(0,0),B=(0,2*sqrt(3)),A=(5,0);
 +
real t = .385, s = 3.5*t-1;
 +
pair R = A*t+B*(1-t), P=B*s;
 +
pair Q = dir(-60) * (R-P) + P;
 +
fill(P--Q--R--cycle,gray);
 +
draw(A--B--C--A^^P--Q--R--P);
 +
dot(A--B--C--P--Q--R);
 +
</asy>
  
 
==Solution 1==
 
==Solution 1==
−
Lemma. If <math>x,y</math> satisfy <math>px+qy=1</math>, then the minimal value of <math>\sqrt{x^2+y^2}</math> is <math>\frac{1}{\sqrt{p^2+q^2}}</math>.
+
Lemma: If <math>x,y</math> satisfy <math>px+qy=1</math>, then the minimal value of <math>\sqrt{x^2+y^2}</math> is <math>\frac{1}{\sqrt{p^2+q^2}}</math>.
  
−
Proof. Recall that the distance between the point <math>(x_0,y_0)</math> and the line <math>px+qy+r = 0</math> is given by <math>\frac{|px_0+qy_0+r|}{\sqrt{p^2+q^2}}</math>. In particular, the distance between the origin and any point <math>(x,y)</math> on the line <math>px+qy=1</math> is at least <math>\frac{1}{\sqrt{p^2+q^2}}</math>.
+
Proof: Recall that the distance between the point <math>(x_0,y_0)</math> and the line <math>px+qy+r = 0</math> is given by <math>\frac{|px_0+qy_0+r|}{\sqrt{p^2+q^2}}</math>. In particular, the distance between the origin and any point <math>(x,y)</math> on the line <math>px+qy=1</math> is at least <math>\frac{1}{\sqrt{p^2+q^2}}</math>.
  
 
---
 
---
  
−
Let the vertices of the right triangle be <math>(0,0),(5,0),(0,2\sqrt{3}),</math> and let <math>(a,0),(0,b)</math> be two of the vertices of the equilateral triangle. Then, the third vertex of the equilateral triangle is <math>\left(\frac{a+\sqrt{3}b}{2},\frac{\sqrt{3}a+b}{2}\right)</math>. This point must lie on the hypotenuse <math>\frac{x}{5} + \frac{y}{2\sqrt{3}} = 1</math>, i.e. <math>a,b</math> must satisfy
+
Let the vertices of the right triangle be <math>(0,0),(5,0),(0,2\sqrt{3}),</math> and let <math>(a,0),(0,b)</math> be the two vertices of the equilateral triangle on the legs of the right triangle. Then, the third vertex of the equilateral triangle is <math>\left(\frac{a+b\sqrt{3}}{2},\frac{a\sqrt{3}+b}{2}\right)</math>. This point must lie on the hypotenuse <math>\frac{x}{5} + \frac{y}{2\sqrt{3}} = 1</math>, i.e. <math>a,b</math> must satisfy
−
<cmath> \frac{a+\sqrt{3}b}{10}+\frac{\sqrt{3}a+b}{4\sqrt{3}} = 1,</cmath>
+
<cmath> \frac{a+b\sqrt{3}}{10}+\frac{a\sqrt{3}+b}{4\sqrt{3}} = 1,</cmath>
 
which can be simplified to
 
which can be simplified to
 
<cmath>\frac{7}{20}a + \frac{11\sqrt{3}}{60}b = 1.</cmath>
 
<cmath>\frac{7}{20}a + \frac{11\sqrt{3}}{60}b = 1.</cmath>
Line 21: Line 32:
 
and hence the answer is <math>75+3+67=\boxed{145}</math>.
 
and hence the answer is <math>75+3+67=\boxed{145}</math>.
  
−
==Solution 2 (No Coordinates)==
+
==Solution 2==
 +
 
 +
Let <math>AB=2\sqrt{3}, BC=5</math>, <math>D</math> lies on <math>BC</math>, <math>F</math> lies on <math>AB</math> and <math>E</math> lies on <math>AC</math>
 +
 
 +
Set <math>D</math> as the origin, <math>BD=a,BF=b</math>, <math>F</math> can be expressed as <math>-a+bi</math> in argand plane, the distance of <math>CD</math> is <math>5-a</math>
 +
 
 +
We know that <math>(-a+bi)\cdot\cos(-\frac{\pi}{3})=(-\frac{a+\sqrt{3}b}{2}+\frac{\sqrt{3}a+b}{2}i)</math>. We know that the slope of <math>AC</math> is <math>-\frac{2\sqrt{3}}{5}</math>, we have that <math>\frac{5-a-(-\frac{a+\sqrt{3}b}{2})}{(\sqrt{3}a+b)/2}=\frac{5}{2\sqrt{3}}</math>, after computation, we have <math>11b+7\sqrt{3}a=20\sqrt{3}</math>
 +
 
 +
Now the rest is easy with C-S inequality, <math>(a^2+b^2)(147+121)\geq (7\sqrt{3}a+11b)^2, a^2+b^2\geq \frac{300}{67}</math> so the smallest area is <math>\frac{\sqrt{3}}{4}\cdot \frac{300}{67}=\frac{75\sqrt{3}}{67}</math>, and the answer is <math>\boxed{145}</math>
 +
 
 +
~bluesoul
 +
 
 +
== Solution 3 ==
 +
 
 +
Let <math>\triangle ABC</math> be the right triangle with sides <math>AB = x</math>, <math>AC = y</math>, and <math>BC = z</math> and right angle at <math>A</math>.
 +
 
 +
Let an equilateral triangle touch <math>AB</math>, <math>AC</math>, and <math>BC</math> at <math>D</math>, <math>E</math>, and <math>F</math> respectively, having side lengths of <math>c</math>.
 +
 
 +
Now, call <math>AD</math> as <math>a</math> and <math>AE</math> as <math>b</math>. Thus, <math>DB = x-a</math> and <math>EC = y-b</math>.
 +
 
 +
By Law of Sines on triangles <math>\triangle DBF</math> and <math>ECF</math>,
 +
 
 +
<math>BF = \frac{z(a\sqrt{3}+b)} {2y}</math> and <math>CF = \frac{z(a+b\sqrt{3})} {2x}</math>.
 +
 
 +
Summing,
 +
 
 +
<math>BF+CF =  \frac{z(a\sqrt{3}+b)} {2y} + \frac{z(a+b\sqrt{3})} {2x} = BC = z</math>.
 +
 
 +
Now substituting <math>AB = x = 2\sqrt{3}</math>, <math>AC = y = 5</math>, and <math>BC = \sqrt{37}</math> and solving,
 +
<math>\frac{7a}{20} + \frac{11b\sqrt{3}}{60} = 1</math>.
 +
 
 +
We seek to minimize <math>[DEF] = c^2 \frac{\sqrt{3}}{4} = (a^2 + b^2) \frac{\sqrt{3}}{4}</math>.
 +
 
 +
This is equivalent to minimizing <math>a^2+b^2</math>.
 +
 
 +
Using the lemma from solution 1, we conclude that <math>\sqrt{a^2+b^2} = \frac{10\sqrt{3}}{\sqrt{67}}</math>
 +
 
 +
Thus, <math>[DEF] = \frac{75\sqrt{3}}{67}</math> and our final answer is <math>\boxed{145}</math>
 +
 
 +
- Awsomness2000
 +
 
 +
==Solution 4 (Trigonometry)==
 +
[[File:2017 AIME I 15.png|530px|right]]
 +
Let <math>ED = DF = x, AC = 5, \angle BAC = \alpha,  \angle CDE = \beta. </math>
 +
 
 +
Then <math>\cot \alpha = \frac {5}{2\sqrt{3}},\angle CDF = \beta - 60^\circ,</math>
 +
<cmath>\angle AED = \beta - \alpha, CD = x \cos(\beta - 60^\circ).</cmath>
 +
 
 +
By Law of Sines on triangle <math>\triangle ADE</math> we get
 +
<cmath>AD = x \frac {\sin (\beta – \alpha)}{\sin{\alpha}}.</cmath>
 +
<cmath>AD + CD = AC \implies </cmath>
 +
<cmath>x(\frac {\sin \beta}{\tan{\alpha}} - \cos \beta) +x (\frac {\cos\beta}{2} +\frac{\sin\beta \sqrt{3}}{2}) = AC</cmath>
 +
<cmath> \implies \frac{AC}{x} = \sin \beta (\cot \alpha + \frac{\sqrt{3}}{2})- \frac{\cos\beta}{2} </cmath>
 +
<cmath>a \sin \beta + b \cos \beta \le \sqrt {a^2+b^2} \implies</cmath>
 +
<cmath>\frac{AC}{x}  \le \sqrt {\left(\cot \alpha + \frac {\sqrt3}{2}\right)^2  + \left(\frac {1}{2}\right)^2} = \sqrt {\cot^2 \alpha + \sqrt {3} \cot \alpha + 1}</cmath>
 +
The smallest area <math>[DEF]</math> is
 +
<cmath>\frac {\sqrt {3}}{4} \cdot x_{min}^2 = \frac {\sqrt {3} AC^2}{4 (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1)} = \frac{75 \sqrt{3}}{67}.</cmath>
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
===Note===
 +
<math>a \sin \beta + b \cos \beta \le \sqrt {a^2+b^2}</math> follows from Cauchy-Schwarz.
 +
<cmath>a \sin \beta + b \cos \beta \le \sqrt{a^2+b^2}\sqrt{\sin^2+\cos^2}=\sqrt{a^2+b^2}</cmath>
 +
~mathboy282
 +
 
 +
== Solution 5 (Complex numbers)==
 +
We will use complex numbers. Set the vertex at the right angle to be the origin, and set the axes so the other two vertices are <math>5</math> and <math>2\sqrt{3}i</math>, respectively. Now let the vertex of the equilateral triangle on the real axis be <math>a</math> and let the vertex of the equilateral triangle on the imaginary axis be <math>bi</math>. Then, the third vertex of the equilateral triangle is given by:
 +
<cmath>(bi-a)e^{-\frac{\pi}{3}i}+a=(bi-a)(\frac{1}{2}-\frac{\sqrt{3}}{2}i)+a=(\frac{a}{2}+\frac{b\sqrt{3}}{2})+(\frac{a\sqrt{3}}{2}+\frac{b}{2})i</cmath>.
 +
 
 +
For this to be on the hypotenuse of the right triangle, we also have the following:
 +
<cmath>\frac{\frac{a\sqrt{3}}{2}+\frac{1}{2}}{\frac{a}{2}+\frac{b\sqrt{3}}{2}-5}=-\frac{2\sqrt{3}}{5}\iff 7\sqrt{3}a+11b=20\sqrt{3}</cmath>
 +
 
 +
Note that the area of the equilateral triangle is given by <math>\frac{\sqrt{3}(a^2+b^2)}{4}</math>, so we seek to minimize <math>a^2+b^2</math>. This can be done by using the Cauchy Schwarz Inequality on the relation we derived above:
 +
<cmath>1200=(7\sqrt{3}a+11b)^2\leq ((7\sqrt{3})^2+11^2)(a^2+b^2)\implies a^2+b^2\geq \frac{1200}{268}</cmath>
 +
 
 +
Thus, the minimum we seek is simply <math>\frac{\sqrt{3}}{4}\cdot\frac{1200}{268}=\frac{75\sqrt{3}}{67}</math>, so the desired answer is <math>\boxed{145}</math>.
 +
 
 +
== Solution 6==
 +
In the complex plane, let the vertices of the triangle be <math>a = 5,</math> <math>b = 2i \sqrt{3},</math> and <math>c = 0.</math> Let <math>e</math> be one of the vertices, where <math>e</math> is real. A point on the line passing through <math>a = 5</math> and <math>b = 2i \sqrt{3}</math> can be expressed in the form
 +
<cmath>f = (1 - t) a + tb = 5(1 - t) + 2ti \sqrt{3}.</cmath>We want the third vertex <math>d</math> to lie on the line through <math>b</math> and <math>c,</math> which is the imaginary axis, so its real part is 0.
 +
Since the small triangle is equilateral, <math>d - e = \cos 60^\circ \cdot (f - e),</math> or
 +
<cmath>d - e = \frac{1 + i \sqrt{3}}{2} \cdot (5(1 - t) - e + 2ti \sqrt{3}).</cmath>Then the real part of <math>d</math> is
 +
<cmath>\frac{5(1 - t) - e}{2} - 3t + e = 0.</cmath>Solving for <math>t</math> in terms of <math>e,</math> we find
 +
<cmath>t = \frac{e + 5}{11}.</cmath>Then
 +
<cmath>f = \frac{5(6 - e)}{11} + \frac{2(e + 5) \sqrt{3}}{11} i,</cmath>so
 +
<cmath>f - e = \frac{30 - 16e}{11} + \frac{2(e + 5) \sqrt{3}}{11} i,</cmath>so
 +
<cmath>\begin{align*}
 +
|f - e|^2 &= \left( \frac{30 - 16e}{11} \right)^2 + \left( \frac{2(e + 5) \sqrt{3}}{11} \right)^2 \\
 +
&= \frac{268e^2 - 840e + 1200}{121}.
 +
\end{align*}</cmath>This quadratic is minimized when <math>e = \frac{840}{2 \cdot 268} = \frac{105}{67},</math> and the minimum is <math>\frac{300}{67},</math> so the smallest area of the equilateral triangle is
 +
<cmath>\frac{\sqrt{3}}{4} \cdot \frac{300}{67} = \boxed{\frac{75 \sqrt{3}}{67}}.</cmath>
 +
 
 +
==Solution 7==
 +
We can use complex numbers. Set the origin at the right angle. Let the point on the real axis be <math>a</math> and the point on the imaginary axis be <math>bi</math>. Then, we see that <math>(a-bi)\left(\text{cis}\frac{\pi}{3}\right)+bi=(a-bi)\left(\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)+bi=\left(\frac{1}{2}a+\frac{\sqrt{3}}{2}b\right)+i\left(\frac{\sqrt{3}}{2}a+\frac{1}{2}b\right).</math> Now we switch back to Cartesian coordinates. The equation of the hypotenuse is <math>y=-\frac{2\sqrt{3}}{5}x+2\sqrt{3}.</math> This means that the point <math>\left(\frac{1}{2}a+\frac{\sqrt{3}}{2}b,\frac{\sqrt{3}}{2}a+\frac{1}{2}b\right)</math> is on the line. Plugging the numbers in, we have <math>\frac{\sqrt{3}}{2}a+\frac{1}{2}b=-\frac{\sqrt{3}}{5}a-\frac{3}{5}b+2\sqrt{3} \implies 7\sqrt{3}a+11b=20\sqrt{3}.</math> Now, we note that the side length of the equilateral triangle is <math>a^2+b^2</math> so it suffices to minimize that. By Cauchy-Schwarz, we have <math>(a^2+b^2)(147+121)\geq(7\sqrt{3}a+11b)^2 \implies (a^2+b^2)\geq\frac{300}{67}.</math> Thus, the area of the smallest triangle is <math>\frac{300}{67}\cdot\frac{\sqrt{3}}{4}=\frac{75\sqrt{3}}{67}</math> so our desired answer is <math>\boxed{145}</math>.
 +
 
 +
(Solution by Pleaseletmetwin, but not added to the Wiki by Pleaseletmetwin)
 +
 
 +
==Solution 8==
 +
Employ the same complex bash as in Solution 5, but instead note that minimizing <math>x^2+y^2</math> is the same as minimizing the distance from
 +
0,0 to x,y, since they are the same quantity. We use point to plane instead, which gives you the required distance.
 +
 
 +
==Solution 9 (Non Analytic)==
  
 
Let <math>S</math> be the triangle with side lengths <math>2\sqrt{3},~5,</math> and <math>\sqrt{37}</math>.
 
Let <math>S</math> be the triangle with side lengths <math>2\sqrt{3},~5,</math> and <math>\sqrt{37}</math>.
Line 27: Line 138:
 
We will think about this problem backwards, by constructing a triangle as large as possible (We will call it <math>T</math>, for convenience) which is similar to <math>S</math> with vertices outside of a unit equilateral triangle <math>\triangle ABC</math>, such that each vertex of the equilateral triangle lies on a side of <math>T</math>. After we find the side lengths of <math>T</math>, we will use ratios to trace back towards the original problem.
 
We will think about this problem backwards, by constructing a triangle as large as possible (We will call it <math>T</math>, for convenience) which is similar to <math>S</math> with vertices outside of a unit equilateral triangle <math>\triangle ABC</math>, such that each vertex of the equilateral triangle lies on a side of <math>T</math>. After we find the side lengths of <math>T</math>, we will use ratios to trace back towards the original problem.
  
−
First of all, let <math>\theta = 90^{\circ}</math>, <math>\alpha = \arctan(\frac{2\sqrt{3}}{5})</math>, and <math>\beta = \arctan(\frac{5}{2\sqrt{3}})</math> (These three angles are simply the angles of triangle <math>S</math>; out of these three angles, <math>\alpha</math> is the smallest angle, and <math>\theta</math> is the largest angle). Then let us consider a point <math>P</math> inside <math>\triangle ABC</math> such that <math>\angle APB = 180^{\circ} - \theta</math>, <math>\angle BPC = 180^{\circ} - \alpha</math>, and <math>\angle APC = 180^{\circ} - \beta</math>. Construct the circumcircles <math>\omega_{AB}, ~\omega_{BC},</math> and <math>\omega_{AC}</math> of triangles <math>APB, ~BPC,</math> and <math>APC</math> respectively.  
+
First of all, let <math>\theta = 90^{\circ}</math>, <math>\alpha = \arctan\left(\frac{2\sqrt{3}}{5}\right)</math>, and <math>\beta = \arctan\left(\frac{5}{2\sqrt{3}}\right)</math> (These three angles are simply the angles of triangle <math>S</math>; out of these three angles, <math>\alpha</math> is the smallest angle, and <math>\theta</math> is the largest angle). Then let us consider a point <math>P</math> inside <math>\triangle ABC</math> such that <math>\angle APB = 180^{\circ} - \theta</math>, <math>\angle BPC = 180^{\circ} - \alpha</math>, and <math>\angle APC = 180^{\circ} - \beta</math>. Construct the circumcircles <math>\omega_{AB}, ~\omega_{BC},</math> and <math>\omega_{AC}</math> of triangles <math>APB, ~BPC,</math> and <math>APC</math> respectively.  
  
 
From here, we will prove the lemma that if we choose points <math>X</math>, <math>Y</math>, and <math>Z</math> on circumcircles <math>\omega_{AB}, ~\omega_{BC},</math> and <math>\omega_{AC}</math> respectively such that <math>X</math>, <math>B</math>, and <math>Y</math> are collinear and <math>Y</math>, <math>C</math>, and <math>Z</math> are collinear, then <math>Z</math>, <math>A</math>, and <math>X</math> must be collinear. First of all, if we let <math>\angle PAX = m</math>, then <math>\angle PBX = 180^{\circ} - m</math> (by the properties of cyclic quadrilaterals), <math>\angle PBY = m</math> (by adjacent angles), <math>\angle PCY = 180^{\circ} - m</math> (by cyclic quadrilaterals), <math>\angle PCZ = m</math> (adjacent angles), and <math>\angle PAZ = 180^{\circ} - m</math> (cyclic quadrilaterals). Since <math>\angle PAX</math> and <math>\angle PAZ</math> are supplementary, <math>Z</math>, <math>A</math>, and <math>X</math> are collinear as desired. Hence, <math>\triangle XYZ</math> has an inscribed equilateral triangle <math>ABC</math>.
 
From here, we will prove the lemma that if we choose points <math>X</math>, <math>Y</math>, and <math>Z</math> on circumcircles <math>\omega_{AB}, ~\omega_{BC},</math> and <math>\omega_{AC}</math> respectively such that <math>X</math>, <math>B</math>, and <math>Y</math> are collinear and <math>Y</math>, <math>C</math>, and <math>Z</math> are collinear, then <math>Z</math>, <math>A</math>, and <math>X</math> must be collinear. First of all, if we let <math>\angle PAX = m</math>, then <math>\angle PBX = 180^{\circ} - m</math> (by the properties of cyclic quadrilaterals), <math>\angle PBY = m</math> (by adjacent angles), <math>\angle PCY = 180^{\circ} - m</math> (by cyclic quadrilaterals), <math>\angle PCZ = m</math> (adjacent angles), and <math>\angle PAZ = 180^{\circ} - m</math> (cyclic quadrilaterals). Since <math>\angle PAX</math> and <math>\angle PAZ</math> are supplementary, <math>Z</math>, <math>A</math>, and <math>X</math> are collinear as desired. Hence, <math>\triangle XYZ</math> has an inscribed equilateral triangle <math>ABC</math>.
Line 52: Line 163:
  
 
'''-Solution by TheBoomBox77'''
 
'''-Solution by TheBoomBox77'''
 +
 +
==Solution 10==
 +
Let the right triangle's lower-left point be at <math>O(0,0)</math>. Notice the 2 other points will determine a unique equilateral triangle. Let 2 points be on the <math>x</math>-axis (<math>B</math>) and the <math>y</math>-axis (<math>A</math>) and label them <math>(b, 0)</math> and <math>(0, a)</math> respectively.  The third point (<math>C</math>) will then be located on the hypotenuse.  We proceed to find the third point's coordinates in terms of <math>a</math> and <math>b</math>.
 +
 +
 +
1. Find the slope of <math>AB</math> and take the negative reciprocal of it to find the slope of the line containing <math>C</math>.  Notice the line contains the midpoint of <math>AB</math> so we can then have an equation of the line.
 +
 +
2. Let <math>AB=x.</math>  For <math>ABC</math> to be an equilateral triangle, the altitude from <math>C</math> to <math>AB</math> must be <math>\frac{x\sqrt{3}}{2}.</math>
 +
 +
We then have two equations and two variables, so we can solve for <math>C</math>'s coordinates.
 +
 +
We can find <math>C(\frac{a+b\sqrt{3}}{2}), (\frac{b+a\sqrt{3}}{2}).</math>
 +
Also, note that <math>C</math> must be on the hypotenuse of the triangle <math>\frac{x}{5}+\frac{y}{2\sqrt{3}}=1.</math>  We can plug in <math>x</math> and <math>y</math> as the coordinates of <math>C</math>,  which simplifies to
 +
 +
<cmath>11b+7\sqrt{3}a=20\sqrt{3}.</cmath> 
 +
 +
We aim to minimize the side length of the triangle, which is <math>\sqrt{a^2+b^2}.</math> Applying the Cauchy inequality gives us
 +
 +
<cmath>(a^2+b^2)(7\sqrt{3}^2+11^2)\geq (11b+7\sqrt3a)^2 = 1200</cmath>
 +
 +
From which we obtain <math>\sqrt{a^2+b^2} \geq \sqrt{\frac{300}{67}}.</math> Thus, the area of the triangle = <math>\frac{75\sqrt{3}}{67}</math> which leads to the answer <math>75+3+67=\boxed{145}.</math>
 +
 +
-hi_im_bob
 +
 +
==Solution 11==
 +
[[File:AIME2017_P15.png|430px|right]]
 +
The general solution to the minimal area is as following:
 +
 +
<cmath>A_{min}={{\sqrt{3}m^2n^2}\over{4(m^2+n^2+\sqrt{3}mn)}},</cmath>
 +
 +
where <math>m</math> and <math>n</math> are the two legs of the right triangle.  In this particular case <math>m=5</math> and <math>n=2\sqrt{3}</math>.  When we plug in these two values, we recover the correct answer of <math>\frac{75\sqrt3}{67}</math>.
 +
 +
The contour of the minimal area <math>A_{min}</math> is plotted as a function of leg lengths <math>m</math> and <math>n</math>, as shown on the right hand side.
 +
 +
===Note===
 +
The proof of the formula can be done in a similar fashion as Solution 4, where instead of using specific values, we define variables, <math>m</math> and <math>n</math> in this case, as per the formula.
 +
 +
==Solution 12 (Geometry)==
 +
[[File:2017 AIME I 15b.png|400px|right]]
 +
Let <math>ED = DF = x, AC = 5, \angle BAC = \alpha.</math>
 +
Then <math>\cot \alpha = \frac {5}{2\sqrt{3}}.</math>
 +
 +
<math>P -</math> midpoint <math>DE, M - </math> midpoint <math>FE, Q -</math> circumcenter <math>\triangle AE.</math>
 +
<cmath>\angle EQM = \alpha, \angle MQE = 90^\circ - \alpha, </cmath>
 +
<cmath>\angle PEQ =  \angle MQE + 60^\circ =  150^\circ - \alpha.</cmath>
 +
<cmath>PE = \frac {x}{2}, QE = \frac {x}{2 \sin \alpha} \implies</cmath>
 +
<cmath>PQ^2 = PE^2 + QE^2 - 2 PE \cdot QE \cdot \cos(150^\circ - \alpha),</cmath>
 +
<cmath>PQ^2 =  \frac{x^2}{4} (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1) .</cmath>
 +
Points <math>P</math> and <math>Q</math> lies on bisectors of <math>CE</math> and <math>AE,</math> so <math>PQ \ge \frac {AC}{2}.</math>
 +
 +
The smallest area <math>[DEF]</math> is
 +
<cmath>\frac {\sqrt {3}}{4} \cdot x_{min}^2 = \frac {\sqrt {3} AC^2}{4 (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1)} = \frac{75 \sqrt{3}}{67}.</cmath>
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
==Solution 13 (Kinematics+Geometry)==
 +
[[File:2017 AIME I 15c.png|430px|right]]
 +
Let <math>ED = DF = x, AC = 5, \angle BAC = \alpha.</math>
 +
Then <math>\cot \alpha = \frac {5}{2\sqrt{3}}.</math>
 +
 +
Let the required triangle with minimal sides <math>DEF</math> be constructed.
 +
 +
Let us vary its position in an acceptable way, that is, we will perform a movement in which the vertices of the <math>\triangle DEF</math> remain on the sides of the <math>\triangle ABC.</math> Any motion of a solid plane figure can be considered as rotation around some point, the center of rotation. The speed of movement of any point is perpendicular to the segment from the center of rotation to this point. With an acceptable variation, the velocities of the vertices of the <math>\triangle DEF</math> are directed along the sides <math>\triangle ABC.</math> Consequently, there is a point <math>X</math> located at the intersection of perpendiculars to the sides of <math>\triangle ABC,</math> around which <math>\triangle DEF</math> rotates. The bases of the perpendiculars dropped from <math>X</math> to the sides of <math>\triangle ABC</math> form a regular <math>\triangle DEF.</math>
 +
 +
Therefore <math>X</math> is the first isodynamic point of <math>\triangle ABC.</math>
 +
 +
It is known that <math>\angle AXB = \angle ACB + 60^\circ = 150^\circ.</math>
 +
 +
The points <math>A, F, X,</math> and <math>E</math> are concyclic, <math>AX</math> is the diameter, so <math>AX = \frac {x}{\sin \alpha}.</math> Similarly,  <math>BX = \frac {x}{\cos \alpha}.</math>
 +
<cmath>AX^2 + BX^2 - 2 AX BX \cos 150^\circ = AB^2, AC = AB \cos \alpha \implies </cmath>
 +
<cmath>AC^2 = x^2 \cdot  (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1).</cmath>
 +
The smallest area <math>[DEF]</math> is
 +
<cmath>\frac {\sqrt {3}}{4} \cdot x_{min}^2 = \frac {\sqrt {3} AC^2}{4 (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1)} = \frac{75 \sqrt{3}}{67}.</cmath>
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
 
==See Also==
 
==See Also==
 
{{AIME box|year=2017|n=I|num-b=14|after=Last Problem}}
 
{{AIME box|year=2017|n=I|num-b=14|after=Last Problem}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 21:06, 10 October 2024

Problem 15

The area of the smallest equilateral triangle with one vertex on each of the sides of the right triangle with side lengths $2\sqrt{3},~5,$ and $\sqrt{37},$ as shown, is $\frac{m\sqrt{p}}{n},$ where $m,~n,$ and $p$ are positive integers, $m$ and $n$ are relatively prime, and $p$ is not divisible by the square of any prime. Find $m+n+p.$

[asy] size(5cm); pair C=(0,0),B=(0,2*sqrt(3)),A=(5,0); real t = .385, s = 3.5*t-1; pair R = A*t+B*(1-t), P=B*s; pair Q = dir(-60) * (R-P) + P; fill(P--Q--R--cycle,gray); draw(A--B--C--A^^P--Q--R--P); dot(A--B--C--P--Q--R); [/asy]

Solution 1

Lemma: If $x,y$ satisfy $px+qy=1$, then the minimal value of $\sqrt{x^2+y^2}$ is $\frac{1}{\sqrt{p^2+q^2}}$.

Proof: Recall that the distance between the point $(x_0,y_0)$ and the line $px+qy+r = 0$ is given by $\frac{|px_0+qy_0+r|}{\sqrt{p^2+q^2}}$. In particular, the distance between the origin and any point $(x,y)$ on the line $px+qy=1$ is at least $\frac{1}{\sqrt{p^2+q^2}}$.

---

Let the vertices of the right triangle be $(0,0),(5,0),(0,2\sqrt{3}),$ and let $(a,0),(0,b)$ be the two vertices of the equilateral triangle on the legs of the right triangle. Then, the third vertex of the equilateral triangle is $\left(\frac{a+b\sqrt{3}}{2},\frac{a\sqrt{3}+b}{2}\right)$. This point must lie on the hypotenuse $\frac{x}{5} + \frac{y}{2\sqrt{3}} = 1$, i.e. $a,b$ must satisfy \[\frac{a+b\sqrt{3}}{10}+\frac{a\sqrt{3}+b}{4\sqrt{3}} = 1,\] which can be simplified to \[\frac{7}{20}a + \frac{11\sqrt{3}}{60}b = 1.\]

By the lemma, the minimal value of $\sqrt{a^2+b^2}$ is \[\frac{1}{\sqrt{\left(\frac{7}{20}\right)^2 + \left(\frac{11\sqrt{3}}{60}\right)^2}} = \frac{10\sqrt{3}}{\sqrt{67}},\] so the minimal area of the equilateral triangle is \[\frac{\sqrt{3}}{4} \cdot \left(\frac{10\sqrt{3}}{\sqrt{67}}\right)^2 = \frac{\sqrt{3}}{4} \cdot \frac{300}{67} = \frac{75\sqrt{3}}{67},\] and hence the answer is $75+3+67=\boxed{145}$.

Solution 2

Let $AB=2\sqrt{3}, BC=5$, $D$ lies on $BC$, $F$ lies on $AB$ and $E$ lies on $AC$

Set $D$ as the origin, $BD=a,BF=b$, $F$ can be expressed as $-a+bi$ in argand plane, the distance of $CD$ is $5-a$

We know that $(-a+bi)\cdot\cos(-\frac{\pi}{3})=(-\frac{a+\sqrt{3}b}{2}+\frac{\sqrt{3}a+b}{2}i)$. We know that the slope of $AC$ is $-\frac{2\sqrt{3}}{5}$, we have that $\frac{5-a-(-\frac{a+\sqrt{3}b}{2})}{(\sqrt{3}a+b)/2}=\frac{5}{2\sqrt{3}}$, after computation, we have $11b+7\sqrt{3}a=20\sqrt{3}$

Now the rest is easy with C-S inequality, $(a^2+b^2)(147+121)\geq (7\sqrt{3}a+11b)^2, a^2+b^2\geq \frac{300}{67}$ so the smallest area is $\frac{\sqrt{3}}{4}\cdot \frac{300}{67}=\frac{75\sqrt{3}}{67}$, and the answer is $\boxed{145}$

~bluesoul

Solution 3

Let $\triangle ABC$ be the right triangle with sides $AB = x$, $AC = y$, and $BC = z$ and right angle at $A$.

Let an equilateral triangle touch $AB$, $AC$, and $BC$ at $D$, $E$, and $F$ respectively, having side lengths of $c$.

Now, call $AD$ as $a$ and $AE$ as $b$. Thus, $DB = x-a$ and $EC = y-b$.

By Law of Sines on triangles $\triangle DBF$ and $ECF$,

$BF = \frac{z(a\sqrt{3}+b)} {2y}$ and $CF = \frac{z(a+b\sqrt{3})} {2x}$.

Summing,

$BF+CF = \frac{z(a\sqrt{3}+b)} {2y} + \frac{z(a+b\sqrt{3})} {2x} = BC = z$.

Now substituting $AB = x = 2\sqrt{3}$, $AC = y = 5$, and $BC = \sqrt{37}$ and solving, $\frac{7a}{20} + \frac{11b\sqrt{3}}{60} = 1$.

We seek to minimize $[DEF] = c^2 \frac{\sqrt{3}}{4} = (a^2 + b^2) \frac{\sqrt{3}}{4}$.

This is equivalent to minimizing $a^2+b^2$.

Using the lemma from solution 1, we conclude that $\sqrt{a^2+b^2} = \frac{10\sqrt{3}}{\sqrt{67}}$

Thus, $[DEF] = \frac{75\sqrt{3}}{67}$ and our final answer is $\boxed{145}$

- Awsomness2000

Solution 4 (Trigonometry)

2017 AIME I 15.png

Let $ED = DF = x, AC = 5, \angle BAC = \alpha, \angle CDE = \beta.$

Then $\cot \alpha = \frac {5}{2\sqrt{3}},\angle CDF = \beta - 60^\circ,$ \[\angle AED = \beta - \alpha, CD = x \cos(\beta - 60^\circ).\]

By Law of Sines on triangle $\triangle ADE$ we get \[AD = x \frac {\sin (\beta – \alpha)}{\sin{\alpha}}.\] \[AD + CD = AC \implies\] \[x(\frac {\sin \beta}{\tan{\alpha}} - \cos \beta) +x (\frac {\cos\beta}{2} +\frac{\sin\beta \sqrt{3}}{2}) = AC\] \[\implies \frac{AC}{x} = \sin \beta (\cot \alpha + \frac{\sqrt{3}}{2})- \frac{\cos\beta}{2}\] \[a \sin \beta + b \cos \beta \le \sqrt {a^2+b^2} \implies\] \[\frac{AC}{x} \le \sqrt {\left(\cot \alpha + \frac {\sqrt3}{2}\right)^2 + \left(\frac {1}{2}\right)^2} = \sqrt {\cot^2 \alpha + \sqrt {3} \cot \alpha + 1}\] The smallest area $[DEF]$ is \[\frac {\sqrt {3}}{4} \cdot x_{min}^2 = \frac {\sqrt {3} AC^2}{4 (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1)} = \frac{75 \sqrt{3}}{67}.\] vladimir.shelomovskii@gmail.com, vvsss

Note

$a \sin \beta + b \cos \beta \le \sqrt {a^2+b^2}$ follows from Cauchy-Schwarz. \[a \sin \beta + b \cos \beta \le \sqrt{a^2+b^2}\sqrt{\sin^2+\cos^2}=\sqrt{a^2+b^2}\] ~mathboy282

Solution 5 (Complex numbers)

We will use complex numbers. Set the vertex at the right angle to be the origin, and set the axes so the other two vertices are $5$ and $2\sqrt{3}i$, respectively. Now let the vertex of the equilateral triangle on the real axis be $a$ and let the vertex of the equilateral triangle on the imaginary axis be $bi$. Then, the third vertex of the equilateral triangle is given by: \[(bi-a)e^{-\frac{\pi}{3}i}+a=(bi-a)(\frac{1}{2}-\frac{\sqrt{3}}{2}i)+a=(\frac{a}{2}+\frac{b\sqrt{3}}{2})+(\frac{a\sqrt{3}}{2}+\frac{b}{2})i\].

For this to be on the hypotenuse of the right triangle, we also have the following: \[\frac{\frac{a\sqrt{3}}{2}+\frac{1}{2}}{\frac{a}{2}+\frac{b\sqrt{3}}{2}-5}=-\frac{2\sqrt{3}}{5}\iff 7\sqrt{3}a+11b=20\sqrt{3}\]

Note that the area of the equilateral triangle is given by $\frac{\sqrt{3}(a^2+b^2)}{4}$, so we seek to minimize $a^2+b^2$. This can be done by using the Cauchy Schwarz Inequality on the relation we derived above: \[1200=(7\sqrt{3}a+11b)^2\leq ((7\sqrt{3})^2+11^2)(a^2+b^2)\implies a^2+b^2\geq \frac{1200}{268}\]

Thus, the minimum we seek is simply $\frac{\sqrt{3}}{4}\cdot\frac{1200}{268}=\frac{75\sqrt{3}}{67}$, so the desired answer is $\boxed{145}$.

Solution 6

In the complex plane, let the vertices of the triangle be $a = 5,$ $b = 2i \sqrt{3},$ and $c = 0.$ Let $e$ be one of the vertices, where $e$ is real. A point on the line passing through $a = 5$ and $b = 2i \sqrt{3}$ can be expressed in the form \[f = (1 - t) a + tb = 5(1 - t) + 2ti \sqrt{3}.\]We want the third vertex $d$ to lie on the line through $b$ and $c,$ which is the imaginary axis, so its real part is 0. Since the small triangle is equilateral, $d - e = \cos 60^\circ \cdot (f - e),$ or \[d - e = \frac{1 + i \sqrt{3}}{2} \cdot (5(1 - t) - e + 2ti \sqrt{3}).\]Then the real part of $d$ is \[\frac{5(1 - t) - e}{2} - 3t + e = 0.\]Solving for $t$ in terms of $e,$ we find \[t = \frac{e + 5}{11}.\]Then \[f = \frac{5(6 - e)}{11} + \frac{2(e + 5) \sqrt{3}}{11} i,\]so \[f - e = \frac{30 - 16e}{11} + \frac{2(e + 5) \sqrt{3}}{11} i,\]so \begin{align*} |f - e|^2 &= \left( \frac{30 - 16e}{11} \right)^2 + \left( \frac{2(e + 5) \sqrt{3}}{11} \right)^2 \\ &= \frac{268e^2 - 840e + 1200}{121}. \end{align*}This quadratic is minimized when $e = \frac{840}{2 \cdot 268} = \frac{105}{67},$ and the minimum is $\frac{300}{67},$ so the smallest area of the equilateral triangle is \[\frac{\sqrt{3}}{4} \cdot \frac{300}{67} = \boxed{\frac{75 \sqrt{3}}{67}}.\]

Solution 7

We can use complex numbers. Set the origin at the right angle. Let the point on the real axis be $a$ and the point on the imaginary axis be $bi$. Then, we see that $(a-bi)\left(\text{cis}\frac{\pi}{3}\right)+bi=(a-bi)\left(\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)+bi=\left(\frac{1}{2}a+\frac{\sqrt{3}}{2}b\right)+i\left(\frac{\sqrt{3}}{2}a+\frac{1}{2}b\right).$ Now we switch back to Cartesian coordinates. The equation of the hypotenuse is $y=-\frac{2\sqrt{3}}{5}x+2\sqrt{3}.$ This means that the point $\left(\frac{1}{2}a+\frac{\sqrt{3}}{2}b,\frac{\sqrt{3}}{2}a+\frac{1}{2}b\right)$ is on the line. Plugging the numbers in, we have $\frac{\sqrt{3}}{2}a+\frac{1}{2}b=-\frac{\sqrt{3}}{5}a-\frac{3}{5}b+2\sqrt{3} \implies 7\sqrt{3}a+11b=20\sqrt{3}.$ Now, we note that the side length of the equilateral triangle is $a^2+b^2$ so it suffices to minimize that. By Cauchy-Schwarz, we have $(a^2+b^2)(147+121)\geq(7\sqrt{3}a+11b)^2 \implies (a^2+b^2)\geq\frac{300}{67}.$ Thus, the area of the smallest triangle is $\frac{300}{67}\cdot\frac{\sqrt{3}}{4}=\frac{75\sqrt{3}}{67}$ so our desired answer is $\boxed{145}$.

(Solution by Pleaseletmetwin, but not added to the Wiki by Pleaseletmetwin)

Solution 8

Employ the same complex bash as in Solution 5, but instead note that minimizing $x^2+y^2$ is the same as minimizing the distance from 0,0 to x,y, since they are the same quantity. We use point to plane instead, which gives you the required distance.

Solution 9 (Non Analytic)

Let $S$ be the triangle with side lengths $2\sqrt{3},~5,$ and $\sqrt{37}$.

We will think about this problem backwards, by constructing a triangle as large as possible (We will call it $T$, for convenience) which is similar to $S$ with vertices outside of a unit equilateral triangle $\triangle ABC$, such that each vertex of the equilateral triangle lies on a side of $T$. After we find the side lengths of $T$, we will use ratios to trace back towards the original problem.

First of all, let $\theta = 90^{\circ}$, $\alpha = \arctan\left(\frac{2\sqrt{3}}{5}\right)$, and $\beta = \arctan\left(\frac{5}{2\sqrt{3}}\right)$ (These three angles are simply the angles of triangle $S$; out of these three angles, $\alpha$ is the smallest angle, and $\theta$ is the largest angle). Then let us consider a point $P$ inside $\triangle ABC$ such that $\angle APB = 180^{\circ} - \theta$, $\angle BPC = 180^{\circ} - \alpha$, and $\angle APC = 180^{\circ} - \beta$. Construct the circumcircles $\omega_{AB}, ~\omega_{BC},$ and $\omega_{AC}$ of triangles $APB, ~BPC,$ and $APC$ respectively.

From here, we will prove the lemma that if we choose points $X$, $Y$, and $Z$ on circumcircles $\omega_{AB}, ~\omega_{BC},$ and $\omega_{AC}$ respectively such that $X$, $B$, and $Y$ are collinear and $Y$, $C$, and $Z$ are collinear, then $Z$, $A$, and $X$ must be collinear. First of all, if we let $\angle PAX = m$, then $\angle PBX = 180^{\circ} - m$ (by the properties of cyclic quadrilaterals), $\angle PBY = m$ (by adjacent angles), $\angle PCY = 180^{\circ} - m$ (by cyclic quadrilaterals), $\angle PCZ = m$ (adjacent angles), and $\angle PAZ = 180^{\circ} - m$ (cyclic quadrilaterals). Since $\angle PAX$ and $\angle PAZ$ are supplementary, $Z$, $A$, and $X$ are collinear as desired. Hence, $\triangle XYZ$ has an inscribed equilateral triangle $ABC$.

In addition, now we know that all triangles $XYZ$ (as described above) must be similar to triangle $S$, as $\angle AXB = \theta$ and $\angle BYC = \alpha$, so we have developed $AA$ similarity between the two triangles. Thus, $\triangle XYZ$ is the triangle similar to $S$ which we were desiring. Our goal now is to maximize the length of $XY$, in order to maximize the area of $XYZ$, to achieve our original goal.

Note that, all triangles $PYX$ are similar to each other if $Y$, $B$, and $X$ are collinear. This is because $\angle PYB$ is constant, and $\angle PXB$ is also a constant value. Then we have $AA$ similarity between this set of triangles. To maximize $XY$, we can instead maximize $PY$, which is simply the diameter of $\omega_{BC}$. From there, we can determine that $\angle PBY = 90^{\circ}$, and with similar logic, $PA$, $PB$, and $PC$ are perpendicular to $ZX$, $XY$, and $YZ$ respectively We have found our desired largest possible triangle $T$.

All we have to do now is to calculate $YZ$, and use ratios from similar triangles to determine the side length of the equilateral triangle inscribed within $S$. First of all, we will prove that $\angle ZPY = \angle ACB + \angle AXB$. By the properties of cyclic quadrilaterals, $\angle AXB = \angle PAB + \angle PBA$, which means that $\angle ACB + \angle AXB = 180^{\circ} - \angle PAC - \angle PBC$. Now we will show that $\angle ZPY = 180^{\circ} - \angle PAC - \angle PBC$. Note that, by cyclic quadrilaterals, $\angle YZP = \angle PAC$ and $\angle ZYP = \angle PBC$. Hence, $\angle ZPY = 180^{\circ} - \angle PAC - \angle PBC$ (since $\angle ZPY + \angle YZP + \angle ZYP = 180^{\circ}$), proving the aforementioned claim. Then, since $\angle ACB = 60^{\circ}$ and $\angle AXB = \theta = 90^{\circ}$, $\angle ZPY = 150^{\circ}$.

Now we calculate $PY$ and $PZ$, which are simply the diameters of circumcircles $\omega_{BC}$ and $\omega_{AC}$, respectively. By the extended law of sines, $PY = \frac{BC}{\sin{BPC}} = \frac{\sqrt{37}}{2\sqrt{3}}$ and $PZ = \frac{CA}{\sin{CPA}} = \frac{\sqrt{37}}{5}$.

We can now solve for $ZY$ with the law of cosines:

\[(ZY)^2 = \frac{37}{25} + \frac{37}{12} - \left(\frac{37}{5\sqrt{3}}\right)\left(-\frac{\sqrt{3}}{2}\right)\]

\[(ZY)^2 = \frac{37}{25} + \frac{37}{12} + \frac{37}{10}\]

\[(ZY)^2 = \frac{37 \cdot 67}{300}\]

\[ZY = \sqrt{37} \cdot \frac{\sqrt{67}}{10\sqrt{3}}\]

Now we will apply this discovery towards our original triangle $S$. Since the ratio between $ZY$ and the hypotenuse of $S$ is $\frac{\sqrt{67}}{10\sqrt{3}}$, the side length of the equilateral triangle inscribed within $S$ must be $\frac{10\sqrt{3}}{\sqrt{67}}$ (as $S$ is simply as scaled version of $XYZ$, and thus their corresponding inscribed equilateral triangles must be scaled by the same factor). Then the area of the equilateral triangle inscribed within $S$ is $\frac{75\sqrt{3}}{67}$, implying that the answer is $\boxed{145}$.

-Solution by TheBoomBox77

Solution 10

Let the right triangle's lower-left point be at $O(0,0)$. Notice the 2 other points will determine a unique equilateral triangle. Let 2 points be on the $x$-axis ($B$) and the $y$-axis ($A$) and label them $(b, 0)$ and $(0, a)$ respectively. The third point ($C$) will then be located on the hypotenuse. We proceed to find the third point's coordinates in terms of $a$ and $b$.


1. Find the slope of $AB$ and take the negative reciprocal of it to find the slope of the line containing $C$. Notice the line contains the midpoint of $AB$ so we can then have an equation of the line.

2. Let $AB=x.$ For $ABC$ to be an equilateral triangle, the altitude from $C$ to $AB$ must be $\frac{x\sqrt{3}}{2}.$

We then have two equations and two variables, so we can solve for $C$'s coordinates.

We can find $C(\frac{a+b\sqrt{3}}{2}), (\frac{b+a\sqrt{3}}{2}).$ Also, note that $C$ must be on the hypotenuse of the triangle $\frac{x}{5}+\frac{y}{2\sqrt{3}}=1.$ We can plug in $x$ and $y$ as the coordinates of $C$, which simplifies to

\[11b+7\sqrt{3}a=20\sqrt{3}.\]

We aim to minimize the side length of the triangle, which is $\sqrt{a^2+b^2}.$ Applying the Cauchy inequality gives us

\[(a^2+b^2)(7\sqrt{3}^2+11^2)\geq (11b+7\sqrt3a)^2 = 1200\]

From which we obtain $\sqrt{a^2+b^2} \geq \sqrt{\frac{300}{67}}.$ Thus, the area of the triangle = $\frac{75\sqrt{3}}{67}$ which leads to the answer $75+3+67=\boxed{145}.$

-hi_im_bob

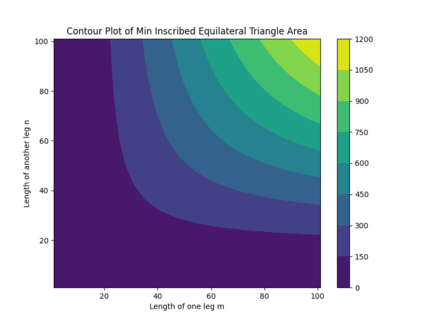
Solution 11

AIME2017 P15.png

The general solution to the minimal area is as following:

\[A_{min}={{\sqrt{3}m^2n^2}\over{4(m^2+n^2+\sqrt{3}mn)}},\]

where $m$ and $n$ are the two legs of the right triangle. In this particular case $m=5$ and $n=2\sqrt{3}$. When we plug in these two values, we recover the correct answer of $\frac{75\sqrt3}{67}$.

The contour of the minimal area $A_{min}$ is plotted as a function of leg lengths $m$ and $n$, as shown on the right hand side.

Note

The proof of the formula can be done in a similar fashion as Solution 4, where instead of using specific values, we define variables, $m$ and $n$ in this case, as per the formula.

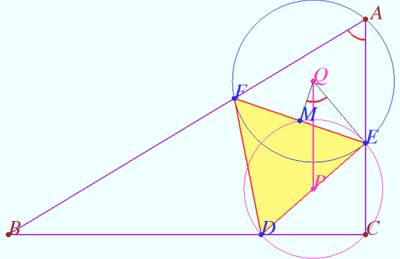
Solution 12 (Geometry)

2017 AIME I 15b.png

Let $ED = DF = x, AC = 5, \angle BAC = \alpha.$ Then $\cot \alpha = \frac {5}{2\sqrt{3}}.$

$P -$ midpoint $DE, M -$ midpoint $FE, Q -$ circumcenter $\triangle AE.$ \[\angle EQM = \alpha, \angle MQE = 90^\circ - \alpha,\] \[\angle PEQ = \angle MQE + 60^\circ = 150^\circ - \alpha.\] \[PE = \frac {x}{2}, QE = \frac {x}{2 \sin \alpha} \implies\] \[PQ^2 = PE^2 + QE^2 - 2 PE \cdot QE \cdot \cos(150^\circ - \alpha),\] \[PQ^2 = \frac{x^2}{4} (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1) .\] Points $P$ and $Q$ lies on bisectors of $CE$ and $AE,$ so $PQ \ge \frac {AC}{2}.$

The smallest area $[DEF]$ is \[\frac {\sqrt {3}}{4} \cdot x_{min}^2 = \frac {\sqrt {3} AC^2}{4 (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1)} = \frac{75 \sqrt{3}}{67}.\] vladimir.shelomovskii@gmail.com, vvsss

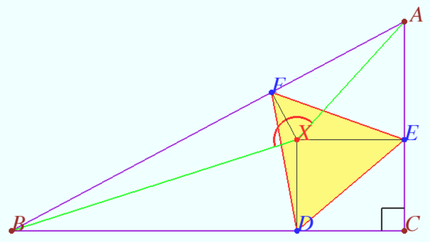
Solution 13 (Kinematics+Geometry)

2017 AIME I 15c.png

Let $ED = DF = x, AC = 5, \angle BAC = \alpha.$ Then $\cot \alpha = \frac {5}{2\sqrt{3}}.$

Let the required triangle with minimal sides $DEF$ be constructed.

Let us vary its position in an acceptable way, that is, we will perform a movement in which the vertices of the $\triangle DEF$ remain on the sides of the $\triangle ABC.$ Any motion of a solid plane figure can be considered as rotation around some point, the center of rotation. The speed of movement of any point is perpendicular to the segment from the center of rotation to this point. With an acceptable variation, the velocities of the vertices of the $\triangle DEF$ are directed along the sides $\triangle ABC.$ Consequently, there is a point $X$ located at the intersection of perpendiculars to the sides of $\triangle ABC,$ around which $\triangle DEF$ rotates. The bases of the perpendiculars dropped from $X$ to the sides of $\triangle ABC$ form a regular $\triangle DEF.$

Therefore $X$ is the first isodynamic point of $\triangle ABC.$

It is known that $\angle AXB = \angle ACB + 60^\circ = 150^\circ.$

The points $A, F, X,$ and $E$ are concyclic, $AX$ is the diameter, so $AX = \frac {x}{\sin \alpha}.$ Similarly, $BX = \frac {x}{\cos \alpha}.$ \[AX^2 + BX^2 - 2 AX BX \cos 150^\circ = AB^2, AC = AB \cos \alpha \implies\] \[AC^2 = x^2 \cdot (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1).\] The smallest area $[DEF]$ is \[\frac {\sqrt {3}}{4} \cdot x_{min}^2 = \frac {\sqrt {3} AC^2}{4 (\cot ^2 \alpha + \sqrt {3} \cot \alpha + 1)} = \frac{75 \sqrt{3}}{67}.\] vladimir.shelomovskii@gmail.com, vvsss

See Also

2017 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2017_AIME_I_Problems/Problem_15&oldid=229557"