Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1983 AHSME Problems/Problem 4"
(→‎See Also)
 
(3 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
== Problem 4 ==
 
== Problem 4 ==
  
−
Position <math>A,B,C,D,E,F</math> such that <math>AF</math> and <math>CD</math> are parallel, as are sides <math>AB</math> and <math>EF</math>,  
+
[[File:pdfresizer.com-pdf-convert.png]]
−
and sides <math>BC</math> and <math>ED</math>. Each side has length of <math>1</math> and it is given that <math>\measuredangle FAB = \measuredangle BCD = 60^\circ</math>.  
+
 
 +
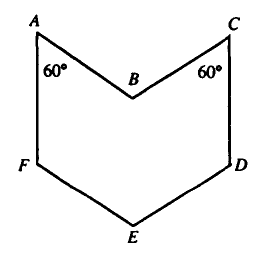
In the adjoining plane figure, sides <math>AF</math> and <math>CD</math> are parallel, as are sides <math>AB</math> and <math>EF</math>,  
 +
and sides <math>BC</math> and <math>ED</math>. Each side has length <math>1</math>. Also, <math>\angle FAB = \angle BCD = 60^\circ</math>.  
 
The area of the figure is  
 
The area of the figure is  
  
 
<math>
 
<math>
−
\text{(A)} \ \frac{\sqrt 3}{2} \qquad  
+
\textbf{(A)} \ \frac{\sqrt 3}{2} \qquad  
−
\text{(B)} \ 1 \qquad  
+
\textbf{(B)} \ 1 \qquad  
−
\text{(C)} \ \frac{3}{2} \qquad  
+
\textbf{(C)} \ \frac{3}{2} \qquad  
−
\text{(D)}\ \sqrt{3}\qquad
+
\textbf{(D)}\ \sqrt{3}\qquad
−
\text{(E)}\ </math>     
+
\textbf{(E)}\ 2</math>     
  
 
[[1983 AHSME Problems/Problem 4|Solution]]
 
[[1983 AHSME Problems/Problem 4|Solution]]
Line 24: Line 26:
 
F = (1, 1.732);
 
F = (1, 1.732);
 
draw(A--B--C--D--E--F--A);
 
draw(A--B--C--D--E--F--A);
−
label("A", A, A);
+
label("$A$", A, NW);
−
label("B", (0.3, 0.866));
+
label("$B$", B, 3W);
−
label("C", (-0.1, 0));
+
label("$C$", C, SW);
−
label("D", D, D);
+
label("$D$", D, SE);
−
label("E", E, E);
+
label("$E$", E, E);
−
label("F", F, F);
+
label("$F$", F, NE);
 
draw(B--D, dashed+linewidth(0.5));
 
draw(B--D, dashed+linewidth(0.5));
 
draw(B--E, dashed+linewidth(0.5));
 
draw(B--E, dashed+linewidth(0.5));
Line 35: Line 37:
 
</asy>
 
</asy>
  
−
Drawing the diagram as described, we create a convex hexagon with all side lengths equal to 1. In this case, it is a natural approach to divide the figure up into four equilateral triangles. The area, A, of one such equilateral triangle is <math>\frac{\sqrt{3}}{4}</math>, which gives a total of <math>4\left(\frac{\sqrt{3}}{4}\right) = \sqrt{3}</math>, or <math>\boxed{D}</math>.
+
By rotating the diagram and drawing the dotted lines, we see that the figure can be divided into four equilateral triangles, each of side length <math>1</math>. The area of one such equilateral triangle is <math>\frac{\sqrt{3}}{4} \cdot 1^2 = \frac{\sqrt{3}}{4}</math>, which gives a total of <math>4\left(\frac{\sqrt{3}}{4}\right) = \sqrt{3}</math>, or <math>\boxed{D}</math>.
  
 
==See Also==
 
==See Also==
Line 41: Line 43:
  
 
{{MAA Notice}}
 
{{MAA Notice}}
 +
 +
[[Category: Introductory Geometry Problems]]

Latest revision as of 05:36, 27 January 2019

Problem 4

Pdfresizer.com-pdf-convert.png

In the adjoining plane figure, sides $AF$ and $CD$ are parallel, as are sides $AB$ and $EF$, and sides $BC$ and $ED$. Each side has length $1$. Also, $\angle FAB = \angle BCD = 60^\circ$. The area of the figure is

$\textbf{(A)} \ \frac{\sqrt 3}{2} \qquad \textbf{(B)} \ 1 \qquad \textbf{(C)} \ \frac{3}{2} \qquad \textbf{(D)}\ \sqrt{3}\qquad \textbf{(E)}\ 2$

Solution

Solution

[asy] pair A, B, C, D, E, F; A = (0, 1.732); B = (0.5, 0.866); C = (0,0); D = (1, 0); E = (1.5, 0.866); F = (1, 1.732); draw(A--B--C--D--E--F--A); label("$A$", A, NW); label("$B$", B, 3W); label("$C$", C, SW); label("$D$", D, SE); label("$E$", E, E); label("$F$", F, NE); draw(B--D, dashed+linewidth(0.5)); draw(B--E, dashed+linewidth(0.5)); draw(B--F, dashed+linewidth(0.5)); [/asy]

By rotating the diagram and drawing the dotted lines, we see that the figure can be divided into four equilateral triangles, each of side length $1$. The area of one such equilateral triangle is $\frac{\sqrt{3}}{4} \cdot 1^2 = \frac{\sqrt{3}}{4}$, which gives a total of $4\left(\frac{\sqrt{3}}{4}\right) = \sqrt{3}$, or $\boxed{D}$.

See Also

1983 AHSME (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
All AHSME Problems and Solutions


The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1983_AHSME_Problems/Problem_4&oldid=100947"