Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AIME I Problems/Problem 6"

(→‎Solution: alt)
m (wik .. cat from number theory/combinatorics -> geometry ..)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
Square <math> ABCD </math> has sides of length 1. Points <math> E </math> and <math> F </math> are on <math> \overline{BC} </math> and <math> \overline{CD}, </math> respectively, so that <math> \triangle AEF </math> is equilateral. A square with vertex <math> B </math> has sides that are parallel to those of <math> ABCD </math> and a vertex on <math> \overline{AE}. </math> The length of a side of this smaller square is <math>\frac{a-\sqrt{b}}{c}, </math> where <math> a, b, </math> and <math> c </math> are positive integers and <math> b</math> is not divisible by the square of any prime. Find <math> a+b+c. </math>
+
[[Square]] <math> ABCD </math> has sides of length 1. Points <math> E </math> and <math> F </math> are on <math> \overline{BC} </math> and <math> \overline{CD}, </math> respectively, so that <math> \triangle AEF </math> is [[equilateral]]. A square with vertex <math> B </math> has sides that are [[parallel]] to those of <math> ABCD </math> and a vertex on <math> \overline{AE}. </math> The length of a side of this smaller square is <math>\frac{a-\sqrt{b}}{c}, </math> where <math> a, b, </math> and <math> c </math> are positive integers and <math> b</math> is not divisible by the square of any prime. Find <math> a+b+c. </math>
  
 
== Solution ==
 
== Solution ==
Line 15: Line 15:
 
{{AIME box|year=2006|n=I|num-b=5|num-a=7}}
 
{{AIME box|year=2006|n=I|num-b=5|num-a=7}}
  
−
[[Category:Intermediate Combinatorics Problems]]
+
[[Category:Intermediate Geometry Problems]]
−
[[Category:Intermediate Number Theory Problems]]
 

Revision as of 16:35, 25 September 2007

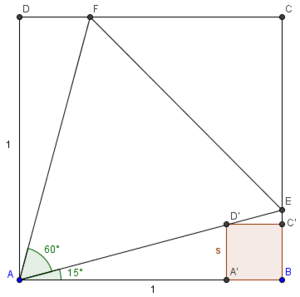
Problem

Square $ABCD$ has sides of length 1. Points $E$ and $F$ are on $\overline{BC}$ and $\overline{CD},$ respectively, so that $\triangle AEF$ is equilateral. A square with vertex $B$ has sides that are parallel to those of $ABCD$ and a vertex on $\overline{AE}.$ The length of a side of this smaller square is $\frac{a-\sqrt{b}}{c},$ where $a, b,$ and $c$ are positive integers and $b$ is not divisible by the square of any prime. Find $a+b+c.$

Solution

2006 I AIME-6.png

Call the vertices of the new square A', B', C', and D', in relation to the vertices of $ABCD$, and define $s$ to be one of the sides of that square. Since the sides are parallel, by corresponding angles and AA~ we know that triangles $AA'D'$ and $D'C'E$ are similar. Thus, the sides are proportional: $\frac{AA'}{A'D'} = \frac{D'C'}{C'E} \Longrightarrow \frac{1 - s}{s} = \frac{s}{1 - s - CE}$. Simplifying, we get that $s^2 = (1 - s)(1 - s - CE)$.

$\angle EAF$ is $60$ degrees, so $\angle BAE = \frac{90 - 60}{2} = 15$. Thus, $\cos 15 = \cos (45 - 30) = \frac{\sqrt{6} + \sqrt{2}}{4} = \frac{1}{AE}$, so $AE = \frac{4}{\sqrt{6} + \sqrt{2}} \cdot \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} - \sqrt{2}} = \sqrt{6} - \sqrt{2}$. Since $\triangle AEF$ is equilateral, $EF = AE = \sqrt{6} - \sqrt{2}$. $\triangle CEF$ is a $45-45-90 \triangle$, so $CE = \frac{AE}{\sqrt{2}} = \sqrt{3} - 1$. Substituting back into the equation from the beginning, we get $s^2 = (1 - s)(2 - \sqrt{3} - s)$, so $(3 - \sqrt{3})s = 2 - \sqrt{3}$. Therefore, $s = \frac{2 - \sqrt{3}}{3 - \sqrt{3}} \cdot \frac{3 + \sqrt{3}}{3 + \sqrt{3}} = \frac{3 - \sqrt{3}}{6}$, and $a + b + c = 3 + 3 + 6 = 012$.

Here's an alternative geometric way to calculate $CE$ (as opposed to trigonometric): The diagonal $\overline{AC}$ is made of the altitude of the equilateral triangle and the altitude of the $45-45-90 \triangle$. The former is $\frac{CE\sqrt{3}}{2}$, and the latter is $\frac{CE}{2}$; thus $\frac{CE\sqrt{3} + CE}{2} = AC = \sqrt{2} \Longrightarrow CE = \sqrt{6}-\sqrt{2}$. The solution continues as above.

See also

2006 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AIME_I_Problems/Problem_6&oldid=16927"