Difference between revisions of "2022 AIME II Problems/Problem 11"
(→Solution) |
|||
| Line 4: | Line 4: | ||
==Solution== | ==Solution== | ||
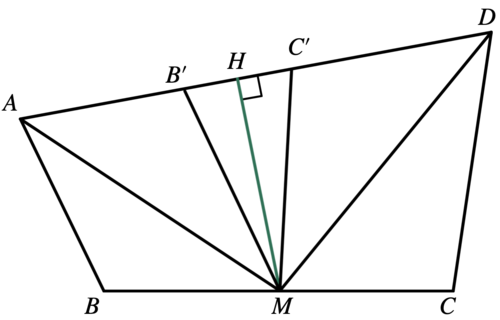
| + | [[Image:2022AIME2-Q11.png|thumb|center|500px|2022 AIME II Q11(Hand-draw picture)]] | ||
| + | |||
| + | According to the problem, we have <math>AB=AB'=2</math>, <math>DC=DC'=3</math>, <math>MB=MB'</math>, <math>MC=MC'</math>, and <math>B'C'=7-2-3=2</math> | ||
| + | |||
| + | Because <math>M</math> is the midpoint of <math>BC</math>, we have <math>BM=MC</math>, so: <cmath>MB=MB'=MC'=MC.</cmath> | ||
| + | |||
| + | Then, we can see that <math>\bigtriangleup{MB'C'}</math> is an isosceles triangle with <math>MB'=MC'</math> | ||
| + | |||
| + | Therefore, we could start our angle chasing: <math>\angle{MB'C'}=\angle{MC'B'}=180^\circ-\angle{MC'D}=180^\circ-\angle{MCD}</math>. | ||
| + | |||
| + | This is when we found that points <math>M</math>, <math>C</math>, <math>D</math>, and <math>B'</math> are on a circle. Thus, <math>\angle{BMB'}=\angle{CDC'} \Rightarrow \angle{B'MA}=\angle{C'DM}</math>. This is the time we found that <math>\bigtriangleup{AB'M} \sim \bigtriangleup{MC'D}</math>. | ||
| + | |||
| + | Thus, <math>\frac{AB'}{B'M}=\frac{MC'}{C'D} \Longrightarrow (BM')^2=AB' \cdot C'D = 6</math> | ||
| + | |||
| + | Point <math>H</math> is the midpoint of <math>B'C'</math>, and <math>MH \perp AD</math>. <math>B'H=HC'=1 \Longrightarrow MH=\sqrt{B'M^2-B'H^2}=\sqrt{6-1}=\sqrt{5}</math>. | ||
| + | |||
| + | The area of this quadrilateral is the sum of areas of triangles: <cmath>S_{\bigtriangleup{ABM}}+S_{\bigtriangleup{AB'M}}+S_{\bigtriangleup{CDM}}+S_{\bigtriangleup{CD'M}}+S_{\bigtriangleup{B'C'M}}</cmath> | ||
| + | <cmath>=S_{\bigtriangleup{AB'M}}\cdot 2 + S_{\bigtriangleup{B'C'M}} + S_{\bigtriangleup{C'DM}}\cdot 2</cmath> | ||
| + | <cmath>=2 \cdot \frac{1}{2} \cdot AB' \cdot MH + \frac{1}{2} \cdot B'C' \cdot MH + 2 \cdot \frac{1}{2} \cdot C'D \cdot MH</cmath> | ||
| + | <cmath>=2\sqrt{5}+\sqrt{5}+3\sqrt{5}=6\sqrt{5}</cmath> | ||
| + | |||
| + | Finally, the square of the area is <math>(6\sqrt{5})^2=\boxed{180}</math> | ||
| + | |||
| + | ~DSAERF-CALMIT | ||
==See Also== | ==See Also== | ||
{{AIME box|year=2022|n=II|num-b=10|num-a=12}} | {{AIME box|year=2022|n=II|num-b=10|num-a=12}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 00:27, 18 February 2022
Problem
Let ![]() be a convex quadrilateral with
be a convex quadrilateral with ![]() ,
, ![]() , and
, and ![]() such that the bisectors of acute angles
such that the bisectors of acute angles ![]() and
and ![]() intersect at the midpoint of
intersect at the midpoint of ![]() . Find the square of the area of
. Find the square of the area of ![]() .
.
Solution
According to the problem, we have ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
Because ![]() is the midpoint of
is the midpoint of ![]() , we have
, we have ![]() , so:
, so: ![]()
Then, we can see that ![]() is an isosceles triangle with
is an isosceles triangle with ![]()
Therefore, we could start our angle chasing: ![]() .
.
This is when we found that points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are on a circle. Thus,
are on a circle. Thus, ![]() . This is the time we found that
. This is the time we found that ![]() .
.
Thus, ![]()
Point ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() .
. ![]() .
.
The area of this quadrilateral is the sum of areas of triangles: ![]()
![]()
![]()
![]()
Finally, the square of the area is ![]()
~DSAERF-CALMIT
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.