Difference between revisions of "2019 AIME II Problems/Problem 7"
(→Solution (Easy to follow)) |
MRENTHUSIASM (talk | contribs) (→Solution 3 (Easy to follow): Removed title for consistency purposes.) |
||
| Line 75: | Line 75: | ||
~ Nafer | ~ Nafer | ||
| − | ==Solution 3 | + | ==Solution 3== |
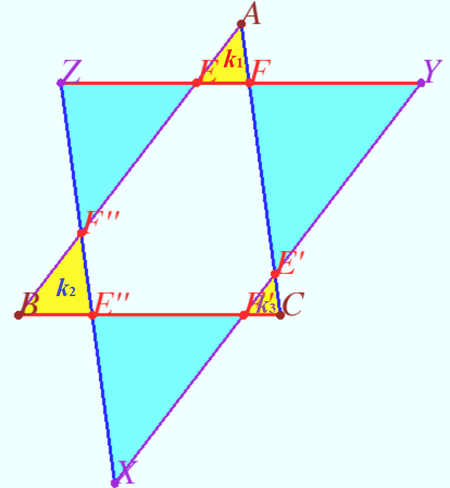
[[File:2019 AIME II 7.png|450px|right]] | [[File:2019 AIME II 7.png|450px|right]] | ||
Notation shown on diagram. By similar triangles we have | Notation shown on diagram. By similar triangles we have | ||
| Line 81: | Line 81: | ||
<cmath>k_2 = \frac{F''E''}{AC} = \frac {BF''}{AB} = \frac{1}{4},</cmath> | <cmath>k_2 = \frac{F''E''}{AC} = \frac {BF''}{AB} = \frac{1}{4},</cmath> | ||
<cmath>k_3 = \frac{E'F'}{AB} = \frac{E'C }{AC} = \frac{1}{8}.</cmath> | <cmath>k_3 = \frac{E'F'}{AB} = \frac{E'C }{AC} = \frac{1}{8}.</cmath> | ||
| − | So <cmath>\frac{ZE}{BC} = \frac{F''E}{AB} = \frac{AB - AE – BF''}{AB} = 1 – k_1 – k_2,</cmath> | + | So, <cmath>\frac{ZE}{BC} = \frac{F''E}{AB} = \frac{AB - AE – BF''}{AB} = 1 – k_1 – k_2,</cmath> |
<cmath>\frac{FY}{BC} = \frac{FE'}{AC} = \frac{AC – AF – CE'}{AC} = 1 – k_1 – k_3.</cmath> | <cmath>\frac{FY}{BC} = \frac{FE'}{AC} = \frac{AC – AF – CE'}{AC} = 1 – k_1 – k_3.</cmath> | ||
<cmath>k = \frac{ZY}{BC} = \frac{ZE + EF + FY}{BC} = (1 – k_1 – k_2) + k_1 + (1 – k_1 – k_3)</cmath> | <cmath>k = \frac{ZY}{BC} = \frac{ZE + EF + FY}{BC} = (1 – k_1 – k_2) + k_1 + (1 – k_1 – k_3)</cmath> | ||
Revision as of 00:53, 12 June 2022
Problem
Triangle ![]() has side lengths
has side lengths ![]() , and
, and ![]() . Lines
. Lines ![]() , and
, and ![]() are drawn parallel to
are drawn parallel to ![]() , and
, and ![]() , respectively, such that the intersections of
, respectively, such that the intersections of ![]() , and
, and ![]() with the interior of
with the interior of ![]() are segments of lengths
are segments of lengths ![]() , and
, and ![]() , respectively. Find the perimeter of the triangle whose sides lie on lines
, respectively. Find the perimeter of the triangle whose sides lie on lines ![]() , and
, and ![]() .
.
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(350); pair A, B, C, D, E, F, G, H, I, J, K, L; B = origin; C = (220,0); A = intersectionpoints(Circle(B,120),Circle(C,180))[0]; D = A+1/4*(B-A); E = A+1/4*(C-A); F = B+1/4*(A-B); G = B+1/4*(C-B); H = C+1/8*(A-C); I = C+1/8*(B-C); J = extension(D,E,F,G); K = extension(F,G,H,I); L = extension(H,I,D,E); draw(A--B--C--cycle); draw(J+9/8*(K-J)--K+9/8*(J-K),dashed); draw(L+9/8*(K-L)--K+9/8*(L-K),dashed); draw(J+9/8*(L-J)--L+9/8*(J-L),dashed); draw(D--E^^F--G^^H--I,red); dot("$B$",B,1.5SW,linewidth(4)); dot("$C$",C,1.5SE,linewidth(4)); dot("$A$",A,1.5N,linewidth(4)); dot(D,linewidth(4)); dot(E,linewidth(4)); dot(F,linewidth(4)); dot(G,linewidth(4)); dot(H,linewidth(4)); dot(I,linewidth(4)); dot(J,linewidth(4)); dot(K,linewidth(4)); dot(L,linewidth(4)); label("$55$",midpoint(D--E),S,red); label("$45$",midpoint(F--G),dir(55),red); label("$15$",midpoint(H--I),dir(160),red); label("$\ell_A$",J+9/8*(L-J),1.5*dir(B--C)); label("$\ell_B$",K+9/8*(J-K),1.5*dir(C--A)); label("$\ell_C$",L+9/8*(K-L),1.5*dir(A--B)); [/asy]](http://latex.artofproblemsolving.com/3/d/c/3dce43af71d1f028005aef8ec9b0ede035a3c8d3.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1
Let the points of intersection of ![]() with
with ![]() divide the sides into consecutive segments
divide the sides into consecutive segments ![]() . Furthermore, let the desired triangle be
. Furthermore, let the desired triangle be ![]() , with
, with ![]() closest to side
closest to side ![]() ,
, ![]() closest to side
closest to side ![]() , and
, and ![]() closest to side
closest to side ![]() . Hence, the desired perimeter is
. Hence, the desired perimeter is ![]() since
since ![]() ,
, ![]() , and
, and ![]() .
.
Note that ![]() , so using similar triangle ratios, we find that
, so using similar triangle ratios, we find that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
We also notice that ![]() and
and ![]() . Using similar triangles, we get that
. Using similar triangles, we get that
![]()
![]()
![]() Hence, the desired perimeter is
Hence, the desired perimeter is ![]() -ktong
-ktong
Solution 2
Let the diagram be set up like that in Solution 1.
By similar triangles we have
![]()
![]() Thus
Thus ![]()
Since ![]() and
and ![]() , the altitude of
, the altitude of ![]() from
from ![]() is half the altitude of
is half the altitude of ![]() from
from ![]() , say
, say ![]() . Also since
. Also since ![]() , the distance from
, the distance from ![]() to
to ![]() is
is ![]() . Therefore the altitude of
. Therefore the altitude of ![]() from
from ![]() is
is
![]() .
.
By triangle scaling, the perimeter of ![]() is
is ![]() of that of
of that of ![]() , or
, or
![]()
~ Nafer
Solution 3
Notation shown on diagram. By similar triangles we have
![]()
![]()
![]() So,
So, ![]()
![]()
![]()
![]()
![]() ~vvsss, www.deoma-cmd.ru
~vvsss, www.deoma-cmd.ru
See Also
| 2019 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.