Difference between revisions of "2022 AIME II Problems/Problem 15"

Revision as of 11:48, 30 August 2022

Problem

Two externally tangent circles $\omega_1$ and $\omega_2$ have centers $O_1$ and $O_2$ , respectively. A third circle $\Omega$ passing through $O_1$ and $O_2$ intersects $\omega_1$ at $B$ and $C$ and $\omega_2$ at $A$ and $D$ , as shown. Suppose that $AB = 2$ , $O_1O_2 = 15$ , $CD = 16$ , and $ABO_1CDO_2$ is a convex hexagon. Find the area of this hexagon. $[asy] import geometry; size(10cm); point O1=(0,0),O2=(15,0),B=9*dir(30); circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B); point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0]; filldraw(A--B--O1--C--D--O2--cycle,0.2*red+white,black); draw(w1); draw(w2); draw(O1--O2,dashed); draw(o); dot(O1); dot(O2); dot(A); dot(D); dot(C); dot(B); label("$\omega_1$",8*dir(110),SW); label("$\omega_2$",5*dir(70)+(15,0),SE); label("$O_1$",O1,W); label("$O_2$",O2,E); label("$B$",B,N+1/2*E); label("$A$",A,N+1/2*W); label("$C$",C,S+1/4*W); label("$D$",D,S+1/4*E); label("$15$",midpoint(O1--O2),N); label("$16$",midpoint(C--D),N); label("$2$",midpoint(A--B),S); label("$\Omega$",o.C+(o.r-1)*dir(270)); [/asy]$

Solution 1

First observe that $AO_2 = O_2D$ and $BO_1 = O_1C$ . Let points $A'$ and $B'$ be the reflections of $A$ and $B$ , respectively, about the perpendicular bisector of $\overline{O_1O_2}$ . Then quadrilaterals $ABO_1O_2$ and $A'B'O_2O_1$ are congruent, so hexagons $ABO_1CDO_2$ and $B'A'O_1CDO_2$ have the same area. Furthermore, triangles $DO_2B'$ and $A'O_1C$ are congruent, so $B'D = A'C$ and quadrilateral $B'A'CD$ is an isosceles trapezoid. $[asy] import olympiad; size(180); defaultpen(linewidth(0.7)); pair Bp = dir(105), Ap = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175); draw(unitcircle^^Bp--Ap--O1--C--D--O2--cycle); label("$B'$",Bp,dir(origin--Bp)); label("$A'$",Ap,dir(origin--Ap)); label("$O_1$",O1,dir(origin--O1)); label("$C$",C,dir(origin--C)); label("$D$",D,dir(origin--D)); label("$O_2$",O2,dir(origin--O2)); draw(O2--O1,linetype("4 4")); draw(Bp--D^^Ap--C,linetype("2 2")); [/asy]$ Next, remark that $A'O_1 = DO_2$ , so quadrilateral $A'O_1DO_2$ is also an isosceles trapezoid; in turn, $A'D = O_1O_2 = 15$ , and similarly $B'C = 15$ . Thus, Ptolmey's theorem on $B'A'CD$ yields $B'D\cdot A'C + 2\cdot 16 = 15^2$ , whence $B'D = A'C = \sqrt{193}$ . Let $\alpha = \angle B'A'D$ . The Law of Cosines on triangle $B'A'D$ yields $\cos\alpha = \frac{15^2 + 2^2 - (\sqrt{193})^2}{2\cdot 2\cdot 15} = \frac{36}{60} = \frac 35,$ and hence $\sin\alpha = \tfrac 45$ . Thus the distance between bases $AB$ and $CD$ is $12$ (in fact, $\triangle B'A'D$ is a $9-12-15$ triangle with a $7-12-\sqrt{193}$ triangle removed), which implies the area of $B'A'CD$ is $\tfrac12\cdot 12\cdot(2+16) = 108$ .

Now let $O_1C = O_2B' = r_1$ and $O_2D = O_1A' = r_2$ ; the tangency of circles $\omega_1$ and $\omega_2$ implies $r_1 + r_2 = 15$ . Furthermore, angles $B'O_2D$ and $B'A'D$ are opposite angles in cyclic quadrilateral $A'B'O_2D$ , which implies the measure of angle $B'O_2D$ is $180^\circ - \alpha$ . Therefore, the Law of Cosines applied to triangle $\triangle B'O_2D$ yields $\begin{align*} 193 &= r_1^2 + r_2^2 - 2r_1r_2(-\tfrac 35) = (r_1^2 + 2r_1r_2 + r_2^2) - \tfrac45r_1r_2\\ &= (r_1+r_2)^2 - \tfrac45 r_1r_2 = 225 - \tfrac45r_1r_2. \end{align*}$

Thus $r_1r_2 = 40$ , and so the area of triangle $B'O_2D$ is $\tfrac12r_1r_2\sin\alpha = 16$ .

Thus, the area of hexagon $ABO_{1}CDO_{2}$ is $108 + 2\cdot 16 = \boxed{140}$ .

~djmathman

Solution 2

Denote by $O$ the center of $\Omega$ . Denote by $r$ the radius of $\Omega$ .

We have $O_1$ , $O_2$ , $A$ , $B$ , $C$ , $D$ are all on circle $\Omega$ .

Denote $\angle O_1 O O_2 = 2 \theta$ . Denote $\angle O_1 O B = \alpha$ . Denote $\angle O_2 O A = \beta$ .

Because $B$ and $C$ are on circles $\omega_1$ and $\Omega$ , $BC$ is a perpendicular bisector of $O_1 O$ . Hence, $\angle O_1 O C = \alpha$ .

Because $A$ and $D$ are on circles $\omega_2$ and $\Omega$ , $AD$ is a perpendicular bisector of $O_2 O$ . Hence, $\angle O_2 O D = \beta$ .

In $\triangle O O_1 O_2$ , $O_1 O_2 = 2 r \sin \theta .$

Hence, $2 r \sin \theta = 15 .$

In $\triangle O AB$ , $\begin{align*} AB & = 2 r \sin \frac{2 \theta - \alpha - \beta}{2} \\ & = 2 r \sin \theta \cos \frac{\alpha + \beta}{2} - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} \\ & = 15 \cos \frac{\alpha + \beta}{2} - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} . \end{align*}$

Hence, $15 \cos \frac{\alpha + \beta}{2} - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} = 2 . \hspace{1cm} (1)$

In $\triangle O CD$ , $\begin{align*} CD & = 2 r \sin \frac{360^\circ - 2 \theta - \alpha - \beta}{2} \\ & = 2 r \sin \left( \theta + \frac{\alpha + \beta}{2} \right) \\ & = 2 r \sin \theta \cos \frac{\alpha + \beta}{2} + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} \\ & = 15 \cos \frac{\alpha + \beta}{2} + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} . \end{align*}$

Hence, $15 \cos \frac{\alpha + \beta}{2} + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} = 16 . \hspace{1cm} (2)$

Taking $\frac{(1) + (2)}{30}$ , we get $\cos \frac{\alpha + \beta}{2} = \frac{3}{5}$ . Thus, $\sin \frac{\alpha + \beta}{2} = \frac{4}{5}$ .

Taking these into (1), we get $2 r \cos \theta = \frac{35}{4}$ . Hence, $\begin{align*} 2 r & = \sqrt{ \left( 2 r \sin \theta \right)^2 + \left( 2 r \cos \theta \right)^2} \\ & = \frac{5}{4} \sqrt{193} . \end{align*}$

Hence, $\cos \theta = \frac{7}{\sqrt{193}}$ .

In $\triangle O O_1 B$ , $O_1 B = 2 r \sin \frac{\alpha}{2} .$

In $\triangle O O_2 A$ , by applying the law of sines, we get $O_2 A = 2 r \sin \frac{\beta}{2} .$

Because circles $\omega_1$ and $\omega_2$ are externally tangent, $B$ is on circle $\omega_1$ , $A$ is on circle $\omega_2$ , $\begin{align*} O_1 O_2 & = O_1 B + O_2 A \\ & = 2 r \sin \frac{\alpha}{2} + 2 r \sin \frac{\beta}{2} \\ & = 2 r \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right) . \end{align*}$

Thus, $\sin \frac{\alpha}{2} + \sin \frac{\beta}{2} = \frac{12}{\sqrt{193}}$ .

Now, we compute $\sin \alpha$ and $\sin \beta$ .

Recall $\cos \frac{\alpha + \beta}{2} = \frac{3}{5}$ and $\sin \frac{\alpha + \beta}{2} = \frac{4}{5}$ . Thus, $e^{i \frac{\alpha}{2}} e^{i \frac{\beta}{2}} = e^{i \frac{\alpha + \beta}{2}} = \frac{3}{5} + i \frac{4}{5}$ .

We also have $\begin{align*} \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} & = \frac{1}{2i} \left( e^{i \frac{\alpha}{2}} - e^{-i \frac{\alpha}{2}} + e^{i \frac{\beta}{2}} - e^{-i \frac{\beta}{2}} \right) \\ & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \frac{\alpha + \beta}{2}} } \right) \left( e^{i \frac{\alpha}{2}} + e^{i \frac{\beta}{2}} \right) . \end{align*}$

Thus, $\begin{align*} \sin \alpha + \sin \beta & = \frac{1}{2i} \left( e^{i \alpha} - e^{-i \alpha} + e^{i \beta} - e^{-i \beta} \right) \\ & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) \left( e^{i \alpha} + e^{i \beta} \right) \\ & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) \left( \left( e^{i \frac{\alpha}{2}} + e^{i \frac{\beta}{2}} \right)^2 - 2 e^{i \frac{\alpha + \beta}{2}} \right) \\ & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) \left( \left( \frac{2 i \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right)}{1 - \frac{1}{e^{i \frac{\alpha + \beta}{2}} }} \right)^2 - 2 e^{i \frac{\alpha + \beta}{2}} \right) \\ & = - \frac{1}{i} \left( e^{i \frac{\alpha + \beta}{2}} - e^{-i \frac{\alpha + \beta}{2}} \right) \left( \frac{2 \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right)^2} {e^{i \frac{\alpha + \beta}{2}} + e^{-i \frac{\alpha + \beta}{2}} - 2 } + 1 \right) \\ & = \frac{167 \cdot 8}{193 \cdot 5 } . \end{align*}$

Therefore, $\begin{align*} {\rm Area} \ ABO_1CDO_2 & = {\rm Area} \ \triangle O_3 AB + {\rm Area} \ \triangle O_3 BO_1 + {\rm Area} \ \triangle O_3 O_1 C \\ & \quad + {\rm Area} \ \triangle O_3 C D + {\rm Area} \ \triangle O_3 D O_2 + {\rm Area} \ \triangle O_3 O_2 A \\ & = \frac{1}{2} r^2 \left( \sin \left( 2 \theta - \alpha - \beta \right) + \sin \alpha + \sin \alpha + \sin \left( 360^\circ - 2 \theta - \alpha - \beta \right) + \sin \beta + \sin \beta \right) \\ & = \frac{1}{2} r^2 \left( \sin \left( 2 \theta - \alpha - \beta \right) - \sin \left( 2 \theta + \alpha + \beta \right) + 2 \sin \alpha + 2 \sin \beta \right) \\ & = r^2 \left( - \cos 2 \theta \sin \left( \alpha + \beta \right) + \sin \alpha + \sin \beta \right) \\ & = r^2 \left( \left( 1 - 2 \cos^2 \theta \right) 2 \sin \frac{\alpha + \beta}{2} \cos \frac{\alpha + \beta}{2} + \sin \alpha + \sin \beta \right) \\ & = \boxed{\textbf{(140) }} . \end{align*}$

~Steven Chen (www.professorchenedu.com)

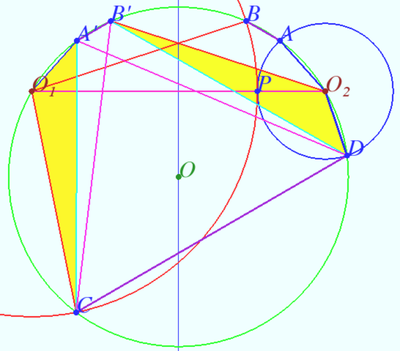
Solution 3

Let points $A'$ and $B'$ be the reflections of $A$ and $B,$ respectively, about the perpendicular bisector of $O_1 O_2.$ $B'O_2 = BO_1 = O_1 P = O_1 C,$ $A'O_1 = AO_2 = O_2 P = O_2 D.$ We establish the equality of the arcs and conclude that the corresponding chords are equal $\overset{\Large\frown} {CO_1} + \overset{\Large\frown} {A'O_1} +\overset{\Large\frown} {A'B'} = \overset{\Large\frown} {B'O_2} +\overset{\Large\frown} {A'O_1} +\overset{\Large\frown} {A'B'} =\overset{\Large\frown} {B'O_2} +\overset{\Large\frown} {DO_2} +\overset{\Large\frown} {A'B'}$ $\implies A'D = B'C = O_1 O_2 = 15.$ Similarly $A'C = B'D \implies \triangle A'CO_1 = \triangle B'DO_2.$

Ptolmey's theorem on $A'CDB'$ yields $B'D \cdot A'C + A'B' \cdot CD = A'D \cdot B'C \implies$ $B'D^2 + 2 \cdot 16 = 15^2 \implies B'D = A'C = \sqrt{193}.$ The area of the trapezoid $A'CDB'$ is equal to the area of an isosceles triangle with sides $A'D = B'C = 15$ and $A'B' + CD = 18.$

The height of this triangle is $\sqrt{15^2-9^2} = 12.$ The area of $A'CDB'$ is $108.$

$\sin \angle B'CD = \frac{12}{15} = \frac{4}{5},$ $\angle B'CD + \angle B'O_2 D = 180^o \implies \sin \angle B'O_2 D = \frac{4}{5}.$

Denote $\angle B'O_2 D = 2\alpha.$ $\angle B'O_2 D > \frac{\pi}{2},$ hence $\cos \angle B'O_2 D = \cos 2\alpha = -\frac{3}{5}.$ $\tan \alpha =\frac { \sin 2 \alpha}{1+\cos 2 \alpha} = \frac {4/5}{1 - 3/5}=2.$

Semiperimeter of $\triangle B'O_2 D$ is $s = \frac {15 + \sqrt{193}}{2}.$

The distance from the vertex $O_2$ to the tangent points of the inscribed circle of the triangle $B'O_2 D$ is equal $s – B'D = \frac{15 – \sqrt{193}}{2}.$

The radius of the inscribed circle is $r = (s – B'D) \tan \alpha.$

The area of triangle $B'O_2 D$ is $[B'O_2 D] = sr = s (s – B'D) \tan \alpha = \frac {15^2 – 193}{2} = 16.$

The hexagon $ABO_1 CDO_2$ has the same area as hexagon $B'A'O_1 CDO_2.$

The area of hexagon $B'A'O_1 CDO_2$ is equal to the sum of the area of the trapezoid $A'CDB'$ and the areas of two equal triangles $B'O_2 D$ and $A'O_1 C,$ so the area of the hexagon $ABO_1 CDO_2$ is $108 + 16 + 16 = \boxed{140}.$

vladimir.shelomovskii@gmail.com, vvsss

@@ Line 285: / Line 285: @@
 The area of hexagon  <math>B'A'O_1 CDO_2</math> is equal to the sum of the area of the trapezoid <math>A'CDB'</math> and the areas of two equal triangles <math>B'O_2 D</math> and <math>A'O_1 C,</math> so the area of the hexagon <math>ABO_1 CDO_2</math>   is <cmath>108 + 16 + 16 = \boxed{140}.</cmath>
-'''Shelomovskii, vvsss,  www.deoma-cmd.ru'''
+'''vladimir.shelomovskii@gmail.com, vvsss'''
 ==See Also==

2022 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search