Difference between revisions of "Euler line"

Revision as of 18:42, 2 November 2022

In any triangle $\triangle ABC$ , the Euler line is a line which passes through the orthocenter $H$ , centroid $G$ , circumcenter $O$ , nine-point center $N$ and de Longchamps point $L$ . It is named after Leonhard Euler. Its existence is a non-trivial fact of Euclidean geometry. Certain fixed orders and distance ratios hold among these points. In particular, $\overline{OGNH}$ and $OG:GN:NH = 2:1:3$

Euler line is the central line $L_{647}$ .

Given the orthic triangle $\triangle H_AH_BH_C$ of $\triangle ABC$ , the Euler lines of $\triangle AH_BH_C$ , $\triangle BH_CH_A$ , and $\triangle CH_AH_B$ concur at $N$ , the nine-point circle of $\triangle ABC$ .

Proof Centroid Lies on Euler Line

This proof utilizes the concept of spiral similarity, which in this case is a rotation followed homothety. Consider the medial triangle $\triangle O_AO_BO_C$ . It is similar to $\triangle ABC$ . Specifically, a rotation of $180^\circ$ about the midpoint of $O_BO_C$ followed by a homothety with scale factor $2$ centered at $A$ brings $\triangle ABC \to \triangle O_AO_BO_C$ . Let us examine what else this transformation, which we denote as $\mathcal{S}$ , will do.

It turns out $O$ is the orthocenter, and $G$ is the centroid of $\triangle O_AO_BO_C$ . Thus, $\mathcal{S}(\{O_A, O, G\}) = \{A, H, G\}$ . As a homothety preserves angles, it follows that $\measuredangle O_AOG = \measuredangle AHG$ . Finally, as $\overline{AH} || \overline{O_AO}$ it follows that $\triangle AHG = \triangle O_AOG$ Thus, $O, G, H$ are collinear, and $\frac{OG}{HG} = \frac{1}{2}$ .

Another Proof

Let $M$ be the midpoint of $BC$ . Extend $CG$ past $G$ to point $H'$ such that $CG = \frac{1}{2} GH$ . We will show $H'$ is the orthocenter. Consider triangles $MGO$ and $AGH'$ . Since $\frac{MG}{GA}=\frac{H'G}{GC} = \frac{1}{2}$ , and they both share a vertical angle, they are similar by SAS similarity. Thus, $AH' \parallel OM \perp BC$ , so $H'$ lies on the $A$ altitude of $\triangle ABC$ . We can analogously show that $H'$ also lies on the $B$ and $C$ altitudes, so $H'$ is the orthocenter.

Proof Nine-Point Center Lies on Euler Line

Assuming that the nine point circle exists and that $N$ is the center, note that a homothety centered at $H$ with factor $2$ brings the Euler points $\{E_A, E_B, E_C\}$ onto the circumcircle of $\triangle ABC$ . Thus, it brings the nine-point circle to the circumcircle. Additionally, $N$ should be sent to $O$ , thus $N \in \overline{HO}$ and $\frac{HN}{ON} = 1$ .

Analytic Proof of Existence

Let the circumcenter be represented by the vector $O = (0, 0)$ , and let vectors $A,B,C$ correspond to the vertices of the triangle. It is well known the that the orthocenter is $H = A+B+C$ and the centroid is $G = \frac{A+B+C}{3}$ . Thus, $O, G, H$ are collinear and $\frac{OG}{HG} = \frac{1}{2}$

Euler line for a triangle with an angle of 120 $^\circ.$

Let the $\angle C$ in triangle $ABC$ be $120^\circ.$ Then the Euler line of the $\triangle ABC$ is parallel to the bisector of $\angle C.$

Proof

Let $\omega$ be circumcircle of $\triangle ABC.$

Let $O$ be circumcenter of $\triangle ABC.$

Let $\omega'$ be the circle symmetric to $\omega$ with respect to $AB.$

Let $E$ be the point symmetric to $O$ with respect to $AB.$

The $\angle C = 120^\circ \implies O$ lies on $\omega', E$ lies on $\omega.$

$EO$ is the radius of $\omega$ and $\omega' \implies$ translation vector $\omega'$ to $\omega$ is $\vec {EO}.$

Let $H'$ be the point symmetric to $H$ with respect to $AB.$ Well known that $H'$ lies on $\omega.$ Therefore point $H$ lies on $\omega'.$

Point $C$ lies on $\omega, CH || OE \implies CH = OE.$

Let $CD$ be the bisector of $\angle C \implies E,O,D$ are concurrent. $OD = HC, OD||HC \implies CD || HO \implies$

Euler line $HO$ of the $\triangle ABC$ is parallel to the bisector $CD$ of $\angle C$ as desired.

vladimir.shelomovskii@gmail.com, vvsss

Concurrent Euler lines and Fermat points

Consider a triangle $ABC$ with Fermat–Torricelli points $F$ and $F'.$ The Euler lines of the $10$ triangles with vertices chosen from $A, B, C, F,$ and $F'$ are concurrent at the centroid $G$ of triangle $ABC.$ We denote centroids by $g$ , circumcenters by $o.$ We use red color for points and lines of triangles $F**,$ green color for triangles $F'**,$ and blue color for triangles $FF'*.$

Case 1

Let $F$ be the first Fermat point of $\triangle ABC$ maximum angle of which smaller then $120^\circ.$ Then the centroid of triangle $ABC$ lies on Euler line of the $\triangle ABF.$ The pairwise angles between these Euler lines are equal $60^\circ.$

Proof

Let $G', O,$ and $\omega$ be centroid, circumcenter, and circumcircle of $\triangle ABF,$ respectevely. Let $\triangle ABD$ be external for $\triangle ABC$ equilateral triangle $\implies F = CD \cap \omega.$ $\angle AFB = 120^\circ \implies AFBD$ is cyclic.

Point $O$ is centroid of $\triangle ABD \implies \vec O = \frac {\vec A + \vec B + \vec D}{3}.$ $\vec G' = \frac {A + B + F}{3}, G = \frac {A + B + C}{3} \implies$ $\vec {OG} = \frac {\vec C – \vec D}{3} = \frac {\vec DC}{3}, \vec {G'G} = \frac {\vec C – \vec F}{3} = \frac {\vec FC}{3} \implies$ $OG||G'G \implies$ Points $O, G',$ and $G$ are colinear, so point $G$ lies on Euler line $OG'$ of $\triangle ABF.$

$\vec {GG_0} = \frac {A – F}{3} \implies GG_0||AF, \vec {GG_1} = \frac {B – F}{3} \implies GG_1||BF.$

Case 2

Let $F$ be the first Fermat point of $\triangle ABC, \angle BAC > 120^\circ.$ Then the centroid $G$ of triangle $ABC$ lies on Euler lines of the triangles $\triangle ABF,\triangle ACF,$ and $\triangle BCF.$ The pairwise angles between these Euler lines are equal $60^\circ.$

Proof

Let $\triangle ABD$ be external for $\triangle ABC$ equilateral triangle, $\omega$ be circumcircle of $\triangle ABD \implies F = CD \cap \omega.$ $\angle ABD = 60^\circ, \angle AFD = 120^\circ \implies ABDF$ is cyclic.

Point $O$ is centroid of $\triangle ABD \implies$ $\vec {OG} = \frac {\vec DC}{3}, \vec {G'G} = \frac {\vec FC}{3} \implies OG||G'G \implies$

Points $O, G',$ and $G$ are colinear, so point $G$ lies on Euler line $OG'$ of $\triangle ABF$ as desired.

Case 3

Let $F'$ be the second Fermat point of $\triangle ABC.$ Then the centroid $G$ of triangle $ABC$ lies on Euler lines of the triangles $\triangle ABF',\triangle ACF',$ and $\triangle BCF'.$ The pairwise angles between these Euler lines are equal $60^\circ.$

Proof

Let $\triangle ABD$ be internal for $\triangle ABC$ equilateral triangle, $\omega$ be circumcircle of $\triangle ABD \implies F' = CD \cap \omega.$

Let $O_1, O_0,$ and $O'$ be circumcenters of the triangles $\triangle ABF',\triangle ACF',$ and $\triangle BCF'.$ Point $O_1$ is centroid of the $\triangle ABD \implies GO_1G_1$ is the Euler line of the $\triangle ABF'$ parallel to $CD.$

$O_1 O_0$ is bisector of $BF', O'O_1$ is bisector of $AF', O'O_0$ is bisector of $CF' \implies \triangle O'O_1O_0$ is regular triangle.

$\triangle O'O_0 O_1$ is the inner Napoleon triangle of the $\triangle ABC \implies G$ is centroid of this regular triangle. $\angle GO_1O_0 = 30^\circ, O_1O_0 \perp F'B, \angle AF'B = 120^\circ \implies GO_0||F'A.$

$\vec {GG_0} = \frac {\vec {F'A}}{3} \implies GG_0||F'A \implies$ points $O_0,G,$ and $G_0$ are collinear as desired.

Similarly, points $O',G,$ and $G'$ are collinear.

Case 4

Let $F$ and $F'$ be the Fermat points of $\triangle ABC.$ Then the centroid of $\triangle ABC$ point $G$ lies on Euler line $OG' (O$ is circumcenter, $G'$ is centroid) of the $\triangle AFF'.$

Proof

Step 1. We find line $F'D$ which is parallel to $GG'.$

Let $M$ be midpoint of $BC.$ Let $M'$ be the midpoint of $FF'.$

Let $D$ be point symmetrical to $F$ with respect to $M.$

$MM'||DF'$ as midline of $\triangle FF'D.$ $\vec {G'G} = \frac {\vec A + \vec B + \vec C}{3} – \frac {\vec A + \vec F + \vec F'}{3} = \frac {2}{3} \cdot (\frac {\vec B + \vec C}{2} – \frac {\vec F + \vec F'}{3})$ $\vec {G'G} = \frac {2}{3} (\vec M – \vec M') = \frac {2}{3} \vec {M'M} \implies M'M||F'D||G'G.$

Step 2. We prove that line $F'D$ is parallel to $OG.$

Let $\triangle xyz$ be the inner Napoleon triangle. Let $\triangle XYZ$ be the outer Napoleon triangle. These triangles are regular centered at $G.$

Points $O, z,$ and $x$ are collinear (they lies on bisector $AF').$

Points $O, Z,$ and $Y$ are collinear (they lies on bisector $AF).$

Points $M, X,$ and $y$ are collinear (they lies on bisector $BC).$ $E = YZ \cap BF, E' = Zx \cap BC.$ $BF \perp XZ \implies \angle BEZ = 30^\circ.$ $BC \perp Xy,$ angle between $Zx$ and $Xy$ is $60^\circ \implies \angle BE'Z = 30^\circ.$

$\angle AF'B = 120^\circ, \overset{\Large\frown} {AZ} = 60^\circ \implies$

Points $A, Z, F', B, E',$ and $E$ are concyclic $\implies \angle OZx = \angle CBF.$ $FM = MD, BM = MC \implies \angle CBF = \angle BCD.$ Points $C, D, X, B,$ and $F'$ are concyclic $\implies \angle BCD = \angle BF'D.$

$\angle GZO = \angle GxO = 30^\circ \implies$ points $Z, O, G,$ and $x$ are concyclic

$\implies \angle GOx = \angle OZx – 30^\circ = \angle AF'B – 30^\circ.$ $\angle AF'B = 120^\circ, Ox \perp AF' \implies OG||F'D.$ Therefore $OG||G'G \implies O, G',$ and $G$ are collinear or point $G$ lies on Euler line $OG'.$

vladimir.shelomovskii@gmail.com, vvsss

Euler line of Gergonne triangle

Prove that the Euler line of Gergonne triangle of $\triangle ABC$ passes through the circumcenter of triangle $ABC.$

Gergonne triangle is also known as the contact triangle or intouch triangle. If the inscribed circle touches the sides of $\triangle ABC$ at points $D, E,$ and $F,$ then $\triangle DEF$ is Gergonne triangle of $\triangle ABC$ .

Other wording: Tangents to circumcircle of $\triangle ABC$ are drawn at the vertices of the triangle. Prove that the circumcenter of the triangle formed by these three tangents lies on the Euler line of the original triangle.

Proof

Let $H$ and $I$ be orthocenter and circumcenter of $\triangle DEF,$ respectively. Let $A'B'C'$ be Orthic Triangle of $\triangle DEF.$

Then $IH$ is Euler line of $\triangle DEF,$ $I$ is the incenter of $\triangle ABC,$ $H$ is the incenter of $\triangle A'B'C'.$

$\angle DEF = \angle DB'C' = \angle BDF = \frac { \overset{\Large\frown} {DF}}{2} \implies B'C' || BC.$

Similarly, $A'C' || AC, A'B' || AB \implies A'B'C'\sim ABC \implies$

$AA' \cap BB' \cap CC' = P,$ where $P$ is the perspector of triangles $ABC$ and $A'B'C'.$

Under homothety with center P and coefficient $\frac {B'C'}{BC}$ the incenter $I$ of $\triangle ABC$ maps into incenter $H$ of $\triangle A'B'C'$ , circumcenter $O$ of $\triangle ABC$ maps into circumcenter $I$ of $\triangle A'B'C' \implies P,H,I,O$ are collinear as desired.

vladimir.shelomovskii@gmail.com, vvsss

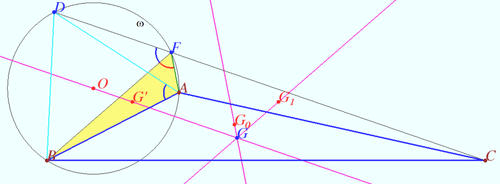
Thebault point

Let $AD, BE,$ and $CF$ be the altitudes of the $\triangle ABC,$ where $BC> AC > AB.$

a) Prove that the Euler lines of triangles $\triangle AEF, \triangle BFD, \triangle CDE$ are concurrent on the nine-point circle at a point T (Thebault point of $\triangle ABC.$ )

b) Prove that $TE = TD + TF.$

Proof

Case 1 Acute triangle

a) It is known, that Euler line of triangle $\triangle ABC$ cross AB and BC (shortest and longest sides) in inner points.

Let $O_0, O,$ and $O'$ be circumcenters of $\triangle AEF, \triangle BFD, \triangle CDE.$

Let $G_0, G,$ and $G'$ be centroids of $\triangle AEF, \triangle BFD, \triangle CDE.$

Denote $\angle ABC = \beta, K = DE \cap G'O', L = EF \cap G_0 O_0, M = EC \cap G'O', \omega$ is the circle $DEF$ (the nine-points circle).

$\angle CEH = \angle CDH = 90^\circ \implies O'$ is the midpoint $CH,$ where $H$ is the orthocenter of $\triangle ABC \implies O' \in \omega.$

Similarly $O_0 \in \omega, O \in \omega.$

$CO' = HO', BO = OH \implies OO'$ is the midline of $\triangle BHC \implies \triangle O_0OO' \sim \triangle ABC.$

Let $O'G'$ cross $\omega$ at point $T$ different from $O'.$

$\triangle ABC \sim \triangle AEF \sim \triangle DBF \sim \triangle DEC \implies$ spiral similarity centered at $E$ maps $\triangle AEF$ onto $\triangle DEC.$

This similarity has the rotation angle $180^\circ – \beta \implies$ acute angle between Euler lines of these triangles is $\beta.$

Let these lines crossed at point $T'.$ Therefore $\angle O_0T'O' = \angle O_0OO' \implies$ points $O, O_0, O',T$ and $T'$ are concyclic $\implies T = T'.$

Similarly, $OG \cap O'G' = T$ as desired.

b) $\triangle AEF \sim \triangle DEC \implies \frac {FL}{LE} = \frac {CM}{ME}.$ Point $G'$ lies on median of $\triangle DEC$ and divide it in proportion 2 : 1.

Point $G'$ lies on Euler line of $\triangle DEC.$

According the Claim, $\frac {DK}{KE}+ \frac {CM}{ME} = 1 \implies \frac {DK}{KE}+ \frac {FL}{LE} = 1.$ $FO_0 = EO_0 \implies \overset{\Large\frown} {FO_0} = \overset{\Large\frown} {EO_0} \implies \angle FTO_0 = \angle ETO_0 \implies \frac {TF}{TE} = \frac {FL}{LE}.$

Similarly $\frac {TD}{TE} = \frac {DK}{KE} \implies \frac {TF}{TE} + \frac {TD}{TE} = 1 \implies TE = TD + TF.$

Claim (Segment crossing the median)

Let $M$ be the midpoint of side $AB$ of the $\triangle ABC, D \in AC,$ $E \in BC, \frac {BE}{CE} = m, \frac {AD}{CD} = n, G = DE \cap CM.$

Then $\frac {DG}{GE} = \frac{1+m}{1+n}, \frac {MG}{GC} = \frac{n+m}{2}.$

Proof

Let $[ABC]$ be $1$ (We use sign $[t]$ to denote the area of $t).$

Denote $[CDG] = x, [CEG] = y, [DGM] = z.$ $[ACM] = [ BCM] = \frac {1}{2}.$ $x = \frac {CD \cdot CG}{2 \cdot CA \cdot CM}, y = \frac {CE \cdot CG}{2 \cdot CB \cdot CM} \implies$ $\frac {DG}{GE} = \frac {x}{y} = \frac {CD \cdot CB}{CA \cdot CE} = \frac {1+m}{1+n}.$ $x + y = \frac {CD \cdot CE}{AC \cdot BC} = \frac {1}{(1+m)(1+n)} \implies$ $x + y = x(1+\frac {y}{x}) = x (1 + \frac {1+n}{1+m} )= \frac {1}{(1+n)(1+m)} \implies x = \frac{1}{(1+n)(2+m+n)}.$ $z+x = \frac {[CDM]}{2[CAM]} = \frac {1}{2(1 + n)}.$ $\frac {MG}{GC} = \frac {z}{x} = \frac {z + x}{x} – 1 =\frac {1}{2(1 + n)} (1+n)(2+m+n) – 1 = \frac {n+m}{2}.$ vladimir.shelomovskii@gmail.com, vvsss

@@ Line 194: / Line 194: @@
 a) It is known, that Euler line of triangle <math>\triangle ABC</math> cross AB and BC (shortest and longest sides) in inner points.
 Let <math>O_0, O,</math> and <math>O'</math> be circumcenters of <math>\triangle AEF, \triangle BFD, \triangle CDE.</math>
 Let <math>G_0, G,</math> and <math>G'</math> be centroids of <math>\triangle AEF, \triangle BFD, \triangle CDE.</math>
-Denote <math>\angle ABC = \beta, \angle BAC = \alpha, K = DF \cap G'O', L = EF \cap G_0 O_0, M = EC \cap G'O',  \omega </math> is the circle <math>DEF</math> (the nine-points circle).
+Denote <math>\angle ABC = \beta, K = DE \cap G'O', L = EF \cap G_0 O_0, M = EC \cap G'O',  \omega </math> is the circle <math>DEF</math> (the nine-points circle).
+<math>\angle CEH = \angle CDH = 90^\circ \implies O'</math> is the midpoint <math>CH,</math> where <math>H</math> is the orthocenter of <math>\triangle ABC \implies O' \in \omega.</math>
+Similarly <math> O_0 \in \omega, O \in \omega.</math>
-<math>\angle CEH = \angle CDH = 90^\circ \implies O'</math> is the midpoint <math>CH,</math> where <math>H</math> is the orthocenter of <math>\triangle ABC \implies O' \in \omega.</math> Similarly <math> O_0 \in \omega, O \in \omega.</math>
+<math>CO'  = HO', BO = OH \implies OO'</math> is the midline of <math>\triangle BHC \implies \triangle O_0OO' \sim \triangle ABC.</math>
-<math>CO'  = HO', BO = OH \implies OO'</math> is midline of <math>\triangle BHC \implies \triangle O_0OO' \sim \triangle ABC.</math>
 Let <math>O'G'</math> cross <math>\omega</math> at point <math>T</math> different from <math>O'.</math>
 <math>\triangle ABC \sim \triangle AEF \sim \triangle DBF \sim  \triangle DEC \implies</math> spiral similarity centered at <math>E</math> maps <math>\triangle AEF</math> onto <math> \triangle DEC.</math>
-This similarity has the rotation angle  <math>180^\circ – \beta \implies</math> acute angle between Euler lines of these triangles is <math>\beta.</math> Let these lines crossed at point <math>T'.</math>
+This similarity has the rotation angle  <math>180^\circ – \beta \implies</math> acute angle between Euler lines of these triangles is <math>\beta.</math>
-Therefore <math>\angle O_0T'O' = \angle O_0OO' \implies </math> points <math>O, O_0, O',T</math>  and <math>T'</math> are conciclic <math>\implies T = T'.</math>
+Let these lines crossed at point <math>T'.</math>
+Therefore <math>\angle O_0T'O' = \angle O_0OO' \implies </math> points <math>O, O_0, O',T</math>  and <math>T'</math> are concyclic <math>\implies T = T'.</math>
-Similarly, <math>OG \cap O'G' = T.</math>
+Similarly, <math>OG \cap O'G' = T</math> as desired.
 b) <math>\triangle AEF \sim  \triangle DEC \implies \frac {FL}{LE} = \frac {CM}{ME}.</math>
@@ Line 216: / Line 224: @@
 Point <math>G'</math> lies on Euler line of <math>\triangle DEC.</math>
-According Claim, <math>\frac {DK}{KE}+ \frac {CM}{ME} = 1 \implies \frac {DK}{KE}+ \frac {FL}{LE} = 1.</math>
+According the <i><b>Claim,</b></i> <math>\frac {DK}{KE}+ \frac {CM}{ME} = 1 \implies \frac {DK}{KE}+ \frac {FL}{LE} = 1.</math>
 <math>FO_0 = EO_0 \implies \overset{\Large\frown} {FO_0} = \overset{\Large\frown} {EO_0} \implies  \angle FTO_0 = \angle ETO_0 \implies   \frac {TF}{TE} =  \frac {FL}{LE}.</math>

Page

Toolbox

Search

Difference between revisions of "Euler line"

Revision as of 18:42, 2 November 2022

Contents

Proof Centroid Lies on Euler Line

Another Proof

Proof Nine-Point Center Lies on Euler Line

Analytic Proof of Existence

Euler line for a triangle with an angle of 120 $^\circ.$

Concurrent Euler lines and Fermat points

Euler line of Gergonne triangle

Thebault point

See also