Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME II Problems/Problem 12"

m
(→‎Video Solution)
Line 39: Line 39:
 
~MathProblemSolvingSkills.com
 
~MathProblemSolvingSkills.com
  
−
 
+
==Video Solution==
 +
https://youtu.be/dx5vgznIyt0
  
 
==See Also==
 
==See Also==
 
{{AIME box|year=2022|n=II|num-b=11|num-a=13}}
 
{{AIME box|year=2022|n=II|num-b=11|num-a=13}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Revision as of 13:30, 15 January 2023

Problem

Let $a, b, x,$ and $y$ be real numbers with $a>4$ and $b>1$ such that\[\frac{x^2}{a^2}+\frac{y^2}{a^2-16}=\frac{(x-20)^2}{b^2-1}+\frac{(y-11)^2}{b^2}=1.\]Find the least possible value of $a+b.$

Solution

Denote \[P(x,y), \qquad \xi_1 : \frac{x^2}{a^2}+\frac{y^2}{a^2-16} = 1, \qquad \xi_2 : \frac{(x-20)^2}{b^2-1}+\frac{(y-11)^2}{b^2} = 1.\]$\xi_1$ is an ellipse whose center is $\left( 0 , 0 \right)$ and foci are $\left( - 4 , 0 \right)$ and $\left( 4 , 0 \right)$. $\xi_2$ is an ellipse whose center is $\left( 20 , 11 \right)$ and foci are $\left( 20 , 10 \right)$ and $\left( 20 , 12 \right)$.

Since $P$ is on $\xi_1$, the sum of distance from $P$ to $\left( - 4 , 0 \right)$ and $\left( 4 , 0 \right)$ is equal to twice the semi-major axis of this ellipse, $2a$.

Since $P$ is on $\xi_2$, the sum of distance from $P$ to $\left( 20 , 10 \right)$ and $\left( 20 , 12 \right)$ is equal to twice the semi-major axis of this ellipse, $2b$.

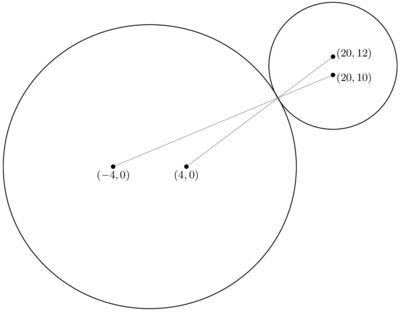
AIME-II-2022-12.png

Therefore, $2a + 2b$ is the sum of the distance from $P$ to four foci of these two ellipses. To minimize this, $P$ must be the intersection point of the line that passes through $\left( - 4 , 0 \right)$ and $\left( 20 , 10 \right)$, and the line that passes through $\left( 4 , 0 \right)$ and $\left( 20 , 12 \right)$.

The distance between $\left( - 4 , 0 \right)$ and $\left( 20 , 10 \right)$ is $\sqrt{\left( 20 + 4 \right)^2 + \left( 10 - 0 \right)^2} = 26$.

The distance between $\left( 4 , 0 \right)$ and $\left( 20 , 12 \right)$ is $\sqrt{\left( 20 - 4 \right)^2 + \left( 12 - 0 \right)^2} = 20$.

Hence, $2 a + 2 b \ge 26 + 20 = 46$, i.e. $a+b\ge 23$.

The straight line connecting the points $\left(–4, 0 \right)$ and $\left(20, 10 \right)$ has the equation $5x+20=12y$. The straight line connecting the points $\left(4, 0 \right)$ and $\left(20, 12 \right)$ has the equation $3x-12=4y$. These lines intersect at the point $\left(14, 15/2 \right)$. This point satisfies both equations for $a = 16, b = 7$. Hence, $a + b = 23$ is possible.

Therefore, $a + b = \boxed{\textbf{023}}.$

~Steven Chen (www.professorchenedu.com)


Video Solution

https://youtu.be/4qiu7GGUGIg

~MathProblemSolvingSkills.com

Video Solution

https://youtu.be/dx5vgznIyt0

See Also

2022 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_II_Problems/Problem_12&oldid=186663"