Difference between revisions of "2013 AIME II Problems/Problem 10"

Latest revision as of 21:42, 15 June 2024

Problem

Given a circle of radius $\sqrt{13}$ , let $A$ be a point at a distance $4 + \sqrt{13}$ from the center $O$ of the circle. Let $B$ be the point on the circle nearest to point $A$ . A line passing through the point $A$ intersects the circle at points $K$ and $L$ . The maximum possible area for $\triangle BKL$ can be written in the form $\frac{a - b\sqrt{c}}{d}$ , where $a$ , $b$ , $c$ , and $d$ are positive integers, $a$ and $d$ are relatively prime, and $c$ is not divisible by the square of any prime. Find $a+b+c+d$ .

Solution 1 (Coordbash)

$[asy] import math; import olympiad; import graph; pair A, B, K, L; B = (sqrt(13), 0); A=(4+sqrt(13), 0); dot(B); dot(A); draw(Circle((0,0), sqrt(13))); label("$O$", (0,0), S);label("$B$", B, SW);label("$A$", A, S); dot((0,0)); [/asy]$

Now we put the figure in the Cartesian plane, let the center of the circle $O (0,0)$ , then $B (\sqrt{13},0)$ , and $A(4+\sqrt{13},0)$

The equation for Circle O is $x^2+y^2=13$ , and let the slope of the line $AKL$ be $k$ , then the equation for line $AKL$ is $y=k(x-4-\sqrt{13})$ .

Then we get $(k^2+1)x^2-2k^2(4+\sqrt{13})x+k^2\cdot (4+\sqrt{13})^2-13=0$ . According to Vieta's Formulas, we get

$x_1+x_2=\frac{2k^2(4+\sqrt{13})}{k^2+1}$ , and $x_1x_2=\frac{(4+\sqrt{13})^2\cdot k^2-13}{k^2+1}$

So, $LK=\sqrt{1+k^2}\cdot \sqrt{(x_1+x_2)^2-4x_1x_2}$

Also, the distance between $B$ and $LK$ is $\frac{k\times \sqrt{13}-(4+\sqrt{13})\cdot k}{\sqrt{1+k^2}}=\frac{-4k}{\sqrt{1+k^2}}$

So the area $S=0.5ah=\frac{-4k\sqrt{(16+8\sqrt{13})k^2-13}}{k^2+1}$

Then the maximum value of $S$ is $\frac{104-26\sqrt{13}}{3}$

So the answer is $104+26+13+3=\boxed{146}$ .

Solution 2

$[asy] import math; import olympiad; import graph; pair A, B, K, L; B = (sqrt(13), 0); A=(4+sqrt(13), 0); dot(B); dot(A); draw(Circle((0,0), sqrt(13))); label("$O$", (0,0), S);label("$B$", B, SW);label("$A$", A, S); dot((0,0)); [/asy]$

Draw $OC$ perpendicular to $KL$ at $C$ . Draw $BD$ perpendicular to $KL$ at $D$ .

$\frac{\triangle OKL}{\triangle BKL} = \frac{OC}{BD} = \frac{AO}{AB} = \frac{4+\sqrt{13}}{4}$

Therefore, to maximize area of $\triangle BKL$ , we need to maximize area of $\triangle OKL$ .

$\triangle OKL = \frac12 r^2 \sin{\angle KOL}$

So when area of $\triangle OKL$ is maximized, $\angle KOL = \frac{\pi}{2}$ .

Eventually, we get $\triangle BKL= \frac12 \cdot (\sqrt{13})^2\cdot(\frac{4}{4+\sqrt{13}})=\frac{104-26\sqrt{13}}{3}$

So the answer is $104+26+13+3=\boxed{146}$ .

Solution 3 (simpler solution)

A rather easier solution is presented in the Girls' Angle WordPress:

http://girlsangle.wordpress.com/2013/11/26/2013-aime-2-problem-10/

Solution 4

Let $N,M$ les on $AL$ such that $BM\bot AL, ON\bot AL$ , call $BM=h, ON=k,LN=KN=d$ We call $\angle{LON}=\alpha$ By similar triangle, we have $\frac{h}{k}=\frac{4}{4+\sqrt{13}}, h=\frac{4k}{4+\sqrt{13}}$ . Then, we realize the area is just $dh=d\cdot \frac{4K}{4+\sqrt{13}}$ As $\sin \alpha=\frac{d}{\sqrt{13}}, \cos \alpha=\frac{k}{\sqrt{13}}$ . Now, we have to maximize $\frac{52\sin \alpha \cos \alpha}{4+\sqrt{13}}=\frac{26\sin 2\alpha}{4+\sqrt{13}}$ , which is obviously reached when $\alpha=45^{\circ}$ , the answer is $\frac{104-26\sqrt{13}}{3}$ leads to $\boxed{146}$

~bluesoul

Solution 5

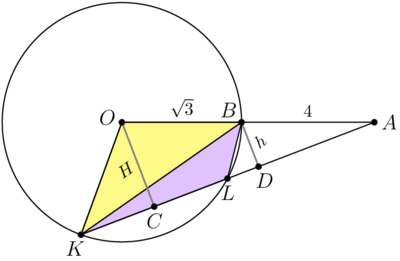
Let C and D be the base of perpendiculars dropped from points O and B to AK. Denote BD = h, OC = H. $\triangle ABD \sim \triangle AOC \implies \frac {h}{H} = \frac {4}{4 + \sqrt{13}}.$ $KL$ is the base of triangles $\triangle OKL$ and $\triangle BKL \implies \frac {[BKL]}{[OKL]} = \frac{h}{H} =$ const $\implies$ The maximum possible area for $\triangle BKL$ and $\triangle OKL$ are at the same position of point $K$ .

$\triangle OKL$ has sides $OK = OL = \sqrt{13}\implies \max[\triangle OKL] = \frac {OK^2}{2} = \frac {13}{2}$

in the case $\angle KOL = 90^\circ.$ It is possible – if we rotate such triangle, we can find position when $A$ lies on $KL.$ $\max[\triangle BKL] = \max[\triangle OKL] \cdot \frac {4}{4+\sqrt{13}} = \frac {26}{4+\sqrt{13}} \implies \boxed{\textbf{146}}$ vladimir.shelomovskii@gmail.com, vvsss

@@ Line 24: / Line 24: @@
 Now we put the figure in the Cartesian plane, let the center of the circle <math>O (0,0)</math>, then <math>B (\sqrt{13},0)</math>, and <math>A(4+\sqrt{13},0)</math>
-The equation for Circle O is <math>x^2+y^2=13</math>, and let the slope of the line<math>AKL</math> be <math>k</math>, then the equation for line<math>AKL</math> is <math>y=k(x-4-\sqrt{13})</math>.
+The equation for Circle O is <math>x^2+y^2=13</math>, and let the slope of the line <math>AKL</math> be <math>k</math>, then the equation for line <math>AKL</math> is <math>y=k(x-4-\sqrt{13})</math>.
 Then we get <math>(k^2+1)x^2-2k^2(4+\sqrt{13})x+k^2\cdot (4+\sqrt{13})^2-13=0</math>. According to [[Vieta's Formulas]], we get

2013 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 9	Followed by Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search