Difference between revisions of "2012 AMC 8 Problems/Problem 5"
(→Solution: That wasn't even a solution before.) |
m (→Solution) |
||
| Line 45: | Line 45: | ||
==Solution== | ==Solution== | ||
[[File:2012amc85.png]] | [[File:2012amc85.png]] | ||
| + | |||
The figure is the same height on both sides, so the sum of the lengths contributing to the height on the left side will equal the sum of the lengths contributing to the height on the left side. | The figure is the same height on both sides, so the sum of the lengths contributing to the height on the left side will equal the sum of the lengths contributing to the height on the left side. | ||
Revision as of 10:17, 23 November 2013
Problem
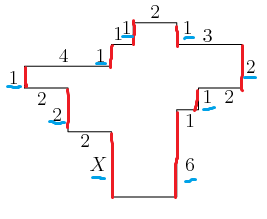
In the diagram, all angles are right angles and the lengths of the sides are given in centimeters. Note the diagram is not drawn to scale. What is , ![]() in centimeters?
in centimeters?
![[asy] pair A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R; A=(4,0); B=(7,0); C=(7,4); D=(8,4); E=(8,5); F=(10,5); G=(10,7); H=(7,7); I=(7,8); J=(5,8); K=(5,7); L=(4,7); M=(4,6); N=(0,6); O=(0,5); P=(2,5); Q=(2,3); R=(4,3); draw(A--B--C--D--E--F--G--H--I--J--K--L--M--N--O--P--Q--R--cycle); label("$X$",(3.4,1.5)); label("6",(7.6,1.5)); label("1",(7.6,3.5)); label("1",(8.4,4.6)); label("2",(9.4,4.6)); label("2",(10.4,6)); label("3",(8.4,7.4)); label("1",(7.5,7.8)); label("2",(6,8.5)); label("1",(4.7,7.8)); label("1",(4.3,7.5)); label("1",(3.5,6.5)); label("4",(1.8,6.5)); label("1",(-0.5,5.5)); label("2",(0.8,4.5)); label("2",(1.5,3.8)); label("2",(2.8,2.6));[/asy]](http://latex.artofproblemsolving.com/b/c/d/bcd57a9d78159bce4d3873f81f5d879beaed1d5a.png)
![]()
Solution
The figure is the same height on both sides, so the sum of the lengths contributing to the height on the left side will equal the sum of the lengths contributing to the height on the left side.

Thus, the answer is ![]() .
.
See Also
| 2012 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()