Difference between revisions of "2005 AMC 10A Problems/Problem 8"
(→Solution) |
(→Solution) |
||
| Line 20: | Line 20: | ||
So, the area of the square is <math>6^2=\boxed{36} \Rightarrow \mathrm{(C)}</math>. | So, the area of the square is <math>6^2=\boxed{36} \Rightarrow \mathrm{(C)}</math>. | ||
| + | ==Video Solution== | ||
CHECK OUT Video Solution: https://youtu.be/z6T9Zm6Jvk0 | CHECK OUT Video Solution: https://youtu.be/z6T9Zm6Jvk0 | ||
Revision as of 20:03, 30 October 2020
Contents
Problem
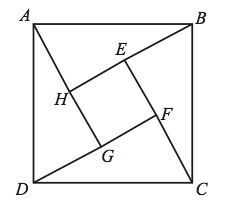
In the figure, the length of side 
of square 
is 
and 
. What is the area of the inner square 
?
Solution
We see that side 
, which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I won’t prove this). So, 
. Then 
, and 
is one of the sides of the square whose area we want to find. So:
![\[1^2 + (HE+1)^2=\sqrt{50}^2\]](http://latex.artofproblemsolving.com/7/c/3/7c37e12e7b6f1641b19a232b4fdbdb6f03349aac.png)
![\[1 + (HE+1)^2=50\]](http://latex.artofproblemsolving.com/2/d/7/2d7e5f6ccce6d23fa35a57d269737c7e9b494cfb.png)
![\[(HE+1)^2=49\]](http://latex.artofproblemsolving.com/c/a/d/cad7941ecb53cad597279cc85a31fa4983b80f0b.png)
![\[HE+1=7\]](http://latex.artofproblemsolving.com/c/e/b/ceb2c8f74471c971c81fcf1364d33b5fbc98787b.png)
![\[HE=6\]](http://latex.artofproblemsolving.com/c/b/0/cb09cde4ae1381e2d11cd524c1aab06d502fb90e.png)
So, the area of the square is 
.
Video Solution
CHECK OUT Video Solution: https://youtu.be/z6T9Zm6Jvk0
See also
| 2005 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
