Difference between revisions of "2021 AIME II Problems/Problem 14"
(→Solution 5 (Why isosceles)) |
(→Solution 5 (Why isosceles)) |
||
| Line 77: | Line 77: | ||
==Solution 5 (Why isosceles)== | ==Solution 5 (Why isosceles)== | ||
| − | + | [[File:2021 AIME II 14.png|230px|right]] | |
| − | [[File:2021 AIME II 14.png| | + | <i><b>Lemma</b></i> |
| + | |||
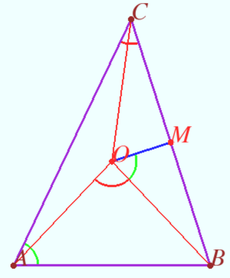
Let <math>\triangle ABC</math> be an acute triangle with circumcenter <math>O.</math> Let <math>M</math> be the midpoint of <math>BC</math> so <math>MO\perp BC.</math> | Let <math>\triangle ABC</math> be an acute triangle with circumcenter <math>O.</math> Let <math>M</math> be the midpoint of <math>BC</math> so <math>MO\perp BC.</math> | ||
| Line 85: | Line 86: | ||
We define <math>\angle AOM</math> as the sum of <math>\angle AOB + \angle BOM,</math> this angle can be greater than <math>\pi.</math> | We define <math>\angle AOM</math> as the sum of <math>\angle AOB + \angle BOM,</math> this angle can be greater than <math>\pi.</math> | ||
| − | + | <i><b>Proof</b></i> | |
| − | < | ||
| − | <math>\angle AOB = 2\angle ACB</math> as | + | <math>\angle BAC = \angle BOM</math> as they share the same intercept <math>\overset{\Large\frown} {BC}</math> (an inscribed angle and half of central angle). |
| + | |||
| + | <math>\angle AOB = 2\angle ACB</math> as they share the same intercept <math>\overset{\Large\frown} {AB}.</math> | ||
<cmath>\angle AOM = \angle AOB + \angle BOM = 2 \angle ACB + \angle CAB.</cmath> | <cmath>\angle AOM = \angle AOB + \angle BOM = 2 \angle ACB + \angle CAB.</cmath> | ||
If <math>\angle AOM = 2 \angle ACB + \angle ABC,</math> then <math>\angle ABC = \angle CAB, AC = BC.</math> | If <math>\angle AOM = 2 \angle ACB + \angle ABC,</math> then <math>\angle ABC = \angle CAB, AC = BC.</math> | ||
| − | + | ||
| + | <i><b>Solution</b></i> | ||
| + | [[File:2021 AIME II proble 14.png|230px|right]] | ||
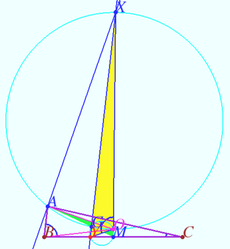
Since <math>\angle OAX = \angle OGX = \frac {\pi}{2},</math> quadrilateral <math>XAGO</math> is cyclic by the Converse of the Inscribed Angle Theorem. | Since <math>\angle OAX = \angle OGX = \frac {\pi}{2},</math> quadrilateral <math>XAGO</math> is cyclic by the Converse of the Inscribed Angle Theorem. | ||
It follows that <math>\angle GXO = \angle GAO,</math> as they share the same intersept <math>\overset{\Large\frown} {GO}.</math> | It follows that <math>\angle GXO = \angle GAO,</math> as they share the same intersept <math>\overset{\Large\frown} {GO}.</math> | ||
Since <math>\angle OGY = \angle OMY = \frac {\pi}{2},</math> quadrilateral <math>OGYM</math> is cyclic by the supplementary opposite angles. | Since <math>\angle OGY = \angle OMY = \frac {\pi}{2},</math> quadrilateral <math>OGYM</math> is cyclic by the supplementary opposite angles. | ||
| − | + | ||
It follows that <math>\angle GYO = \angle OMG,</math> as they share the same intercept <math>\overset{\Large\frown} {GO}.</math> | It follows that <math>\angle GYO = \angle OMG,</math> as they share the same intercept <math>\overset{\Large\frown} {GO}.</math> | ||
In triangles <math>\triangle XOY</math> and <math>\triangle AOM,</math> two pairs of angles are equal, which means that the third angles <math>\angle XOY = \angle AOM</math> are also equal. | In triangles <math>\triangle XOY</math> and <math>\triangle AOM,</math> two pairs of angles are equal, which means that the third angles <math>\angle XOY = \angle AOM</math> are also equal. | ||
| + | |||
<math>\angle ABC : \angle BCA : \angle AOM = 13 : 2 : 17,</math> so <math>\angle AOM = \angle ABC + 2 \angle BCA.</math> | <math>\angle ABC : \angle BCA : \angle AOM = 13 : 2 : 17,</math> so <math>\angle AOM = \angle ABC + 2 \angle BCA.</math> | ||
| + | |||
According to the lemma, <math>\triangle ABC</math> is isosceles, | According to the lemma, <math>\triangle ABC</math> is isosceles, | ||
<cmath>\angle ABC : \angle BCA : \angle BAC = 13 : 2 : 13.</cmath> | <cmath>\angle ABC : \angle BCA : \angle BAC = 13 : 2 : 13.</cmath> | ||
| − | <cmath>\angle BAC = \frac{13} {13 + 2 + 13} \cdot 180^ | + | <cmath>\angle BAC = \frac{13} {13 + 2 + 13} \cdot 180^\circ = \frac {585^\circ}{7}.</cmath> |
Revision as of 01:31, 10 June 2022
Contents
Problem
Let ![]() be an acute triangle with circumcenter
be an acute triangle with circumcenter ![]() and centroid
and centroid ![]() . Let
. Let ![]() be the intersection of the line tangent to the circumcircle of
be the intersection of the line tangent to the circumcircle of ![]() at
at ![]() and the line perpendicular to
and the line perpendicular to ![]() at
at ![]() . Let
. Let ![]() be the intersection of lines
be the intersection of lines ![]() and
and ![]() . Given that the measures of
. Given that the measures of ![]() and
and ![]() are in the ratio
are in the ratio ![]() the degree measure of
the degree measure of ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(375); pair A, B, C, O, G, X, Y; A = origin; B = (1,0); C = extension(A,A+10*dir(585/7),B,B+10*dir(180-585/7)); O = circumcenter(A,B,C); G = centroid(A,B,C); Y = intersectionpoint(G--G+(100,0),B--C); X = intersectionpoint(G--G-(100,0),A--scale(100)*rotate(90)*dir(O-A)); markscalefactor=3/160; draw(rightanglemark(O,G,X),red); dot("$A$",A,1.5*dir(180+585/7),linewidth(4)); dot("$B$",B,1.5*dir(-585/7),linewidth(4)); dot("$C$",C,1.5N,linewidth(4)); dot("$O$",O,1.5N,linewidth(4)); dot("$G$",G,1.5S,linewidth(4)); dot("$Y$",Y,1.5E,linewidth(4)); dot("$X$",X,1.5W,linewidth(4)); draw(A--B--C--cycle^^X--O--Y--cycle^^A--X^^O--G^^circumcircle(A,B,C)); [/asy]](http://latex.artofproblemsolving.com/f/0/5/f0519e337893dd856908a43b2cb78725f49b65ef.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1
In this solution, all angle measures are in degrees.
Let ![]() be the midpoint of
be the midpoint of ![]() so that
so that ![]() and
and ![]() are collinear. Let
are collinear. Let ![]() and
and ![]()
Note that:
- Since
 quadrilateral
quadrilateral  is cyclic by the Converse of the Inscribed Angle Theorem.
is cyclic by the Converse of the Inscribed Angle Theorem.It follows that
 as they share the same intercepted arc
as they share the same intercepted arc 
- Since
 quadrilateral
quadrilateral  is cyclic by the supplementary opposite angles.
is cyclic by the supplementary opposite angles.It follows that
 as they share the same intercepted arc
as they share the same intercepted arc 
Together, we conclude that ![]() by AA, so
by AA, so ![]()
Next, we express ![]() in terms of
in terms of ![]() By angle addition, we have
By angle addition, we have
 Substituting back gives
Substituting back gives ![]() from which
from which ![]()
For the sum of the interior angles of ![]() we get
we get
 Finally, we obtain
Finally, we obtain ![]() from which the answer is
from which the answer is ![]()
~Constance-variance (Fundamental Logic)
~MRENTHUSIASM (Reconstruction)
Solution 2
Let ![]() be the midpoint of
be the midpoint of ![]() . Because
. Because ![]() ,
, ![]() and
and ![]() are cyclic, so
are cyclic, so ![]() is the center of the spiral similarity sending
is the center of the spiral similarity sending ![]() to
to ![]() , and
, and ![]() . Because
. Because ![]() , it's easy to get
, it's easy to get ![]() from here.
from here.
~Lcz
Solution 3 (Easy and Simple)
Firstly, let ![]() be the midpoint of
be the midpoint of ![]() . Then,
. Then, ![]() . Now, note that since
. Now, note that since ![]() , quadrilateral
, quadrilateral ![]() is cyclic. Also, because
is cyclic. Also, because ![]() ,
, ![]() is also cyclic. Now, we define some variables: let
is also cyclic. Now, we define some variables: let ![]() be the constant such that
be the constant such that ![]() and
and ![]() . Also, let
. Also, let ![]() and
and ![]() (due to the fact that
(due to the fact that ![]() and
and ![]() are cyclic). Then,
are cyclic). Then, ![]() Now, because
Now, because ![]() is tangent to the circumcircle at
is tangent to the circumcircle at ![]() ,
, ![]() , and
, and ![]() . Finally, notice that
. Finally, notice that ![]() . Then,
. Then, ![]() Thus,
Thus, ![]() and
and ![]() However, from before,
However, from before, ![]() , so
, so ![]() . To finish the problem, we simply compute
. To finish the problem, we simply compute ![]() so our final answer is
so our final answer is ![]() .
.
~advanture
Solution 4 (Guessing in the Last 3 Minutes, Unreliable)
Notice that ![]() looks isosceles, so we assume it's isosceles. Then, let
looks isosceles, so we assume it's isosceles. Then, let ![]() and
and ![]() Taking the sum of the angles in the triangle gives
Taking the sum of the angles in the triangle gives ![]() so
so ![]() so the answer is
so the answer is ![]()
Solution 5 (Why isosceles)
Lemma
Let ![]() be an acute triangle with circumcenter
be an acute triangle with circumcenter ![]() Let
Let ![]() be the midpoint of
be the midpoint of ![]() so
so ![]()
If ![]() then
then ![]()
We define ![]() as the sum of
as the sum of ![]() this angle can be greater than
this angle can be greater than ![]()
Proof
![]() as they share the same intercept
as they share the same intercept ![]() (an inscribed angle and half of central angle).
(an inscribed angle and half of central angle).
![]() as they share the same intercept
as they share the same intercept ![]()
![]()
If ![]() then
then ![]()
Solution
Since ![]() quadrilateral
quadrilateral ![]() is cyclic by the Converse of the Inscribed Angle Theorem.
is cyclic by the Converse of the Inscribed Angle Theorem.
It follows that ![]() as they share the same intersept
as they share the same intersept ![]() Since
Since ![]() quadrilateral
quadrilateral ![]() is cyclic by the supplementary opposite angles.
is cyclic by the supplementary opposite angles.
It follows that ![]() as they share the same intercept
as they share the same intercept ![]()
In triangles ![]() and
and ![]() two pairs of angles are equal, which means that the third angles
two pairs of angles are equal, which means that the third angles ![]() are also equal.
are also equal.
![]() so
so ![]()
According to the lemma, ![]() is isosceles,
is isosceles,
![]()
![]()
~vvsss, www.deoma-cmd.ru
Video Solution 1
https://www.youtube.com/watch?v=zFH1Z7Ydq1s
~Mathematical Dexterity
Video Solution 2
https://www.youtube.com/watch?v=7Bxr2h4btWo
~Osman Nal
See Also
| 2021 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.