Difference between revisions of "2022 AIME II Problems/Problem 11"

Revision as of 13:02, 18 June 2022

Problem

Let $ABCD$ be a convex quadrilateral with $AB=2$ , $AD=7$ , and $CD=3$ such that the bisectors of acute angles $\angle{DAB}$ and $\angle{ADC}$ intersect at the midpoint of $\overline{BC}$ . Find the square of the area of $ABCD$ .

Solution 1

2022 AIME II Q11(Hand-drawn picture)

According to the problem, we have $AB=AB'=2$ , $DC=DC'=3$ , $MB=MB'$ , $MC=MC'$ , and $B'C'=7-2-3=2$

Because $M$ is the midpoint of $BC$ , we have $BM=MC$ , so: $MB=MB'=MC'=MC.$

Then, we can see that $\bigtriangleup{MB'C'}$ is an isosceles triangle with $MB'=MC'$

Therefore, we could start our angle chasing: $\angle{MB'C'}=\angle{MC'B'}=180^\circ-\angle{MC'D}=180^\circ-\angle{MCD}$ .

This is when we found that points $M$ , $C$ , $D$ , and $B'$ are on a circle. Thus, $\angle{BMB'}=\angle{CDC'} \Rightarrow \angle{B'MA}=\angle{C'DM}$ . This is the time we found that $\bigtriangleup{AB'M} \sim \bigtriangleup{MC'D}$ .

Thus, $\frac{AB'}{B'M}=\frac{MC'}{C'D} \Longrightarrow (BM')^2=AB' \cdot C'D = 6$

Point $H$ is the midpoint of $B'C'$ , and $MH \perp AD$ . $B'H=HC'=1 \Longrightarrow MH=\sqrt{B'M^2-B'H^2}=\sqrt{6-1}=\sqrt{5}$ .

The area of this quadrilateral is the sum of areas of triangles: $S_{\bigtriangleup{ABM}}+S_{\bigtriangleup{AB'M}}+S_{\bigtriangleup{CDM}}+S_{\bigtriangleup{CD'M}}+S_{\bigtriangleup{B'C'M}}$ $=S_{\bigtriangleup{AB'M}}\cdot 2 + S_{\bigtriangleup{B'C'M}} + S_{\bigtriangleup{C'DM}}\cdot 2$ $=2 \cdot \frac{1}{2} \cdot AB' \cdot MH + \frac{1}{2} \cdot B'C' \cdot MH + 2 \cdot \frac{1}{2} \cdot C'D \cdot MH$ $=2\sqrt{5}+\sqrt{5}+3\sqrt{5}=6\sqrt{5}$

Finally, the square of the area is $(6\sqrt{5})^2=\boxed{180}$

~DSAERF-CALMIT (https://binaryphi.site)

Solution 2

Denote by $M$ the midpoint of segment $BC$ . Let points $P$ and $Q$ be on segment $AD$ , such that $AP = AB$ and $DQ = DC$ .

Denote $\angle DAM = \alpha$ , $\angle BAD = \beta$ , $\angle BMA = \theta$ , $\angle CMD = \phi$ .

Denote $BM = x$ . Because $M$ is the midpoint of $BC$ , $CM = x$ .

Because $AM$ is the angle bisector of $\angle BAD$ and $AB = AP$ , $\triangle BAM \cong \triangle PAM$ . Hence, $MP = MB$ and $\angle AMP = \theta$ . Hence, $\angle MPD = \angle MAP + \angle PMA = \alpha + \theta$ .

Because $DM$ is the angle bisector of $\angle CDA$ and $DC = DQ$ , $\triangle CDM \cong \triangle QDM$ . Hence, $MQ = MC$ and $\angle DMQ = \phi$ . Hence, $\angle MQA = \angle MDQ + \angle QMD = \beta + \phi$ .

Because $M$ is the midpoint of segment $BC$ , $MB = MC$ . Because $MP = MB$ and $MQ = MC$ , $MP = MQ$ .

Thus, $\angle MPD = \angle MQA$ .

Thus, $\alpha + \theta = \beta + \phi . \hspace{1cm} (1)$

In $\triangle AMD$ , $\angle AMD = 180^\circ - \angle MAD - \angle MDA = 180^\circ - \alpha - \beta$ . In addition, $\angle AMD = 180^\circ - \angle BMA - \angle CMD = 180^\circ - \theta - \phi$ . Thus, $\alpha + \beta = \theta + \phi . \hspace{1cm} (2)$

Taking $(1) + (2)$ , we get $\alpha = \phi$ . Taking $(1) - (2)$ , we get $\beta = \theta$ .

Therefore, $\triangle ADM \sim \triangle AMB \sim \triangle MDC$ .

Hence, $\frac{AD}{AM} = \frac{AM}{AB}$ and $\frac{AD}{DM} = \frac{DM}{CD}$ . Thus, $AM = \sqrt{AD \cdot AD} = \sqrt{14}$ and $DM = \sqrt{AD \cdot CD} = \sqrt{21}$ .

In $\triangle ADM$ , by applying the law of cosines, $\cos \angle AMD = \frac{AM^2 + DM^2 - AD^2}{2 AM \cdot DM} = - \frac{1}{\sqrt{6}}$ . Hence, $\sin \angle AMD = \sqrt{1 - \cos^2 \angle AMD} = \frac{\sqrt{5}}{\sqrt{6}}$ . Hence, ${\rm Area} \ \triangle ADM = \frac{1}{2} AM \cdot DM \dot \sin \angle AMD = \frac{7 \sqrt{5}}{2}$ .

Therefore, $\begin{align*} {\rm Area} \ ABCD & = {\rm Area} \ \triangle AMD + {\rm Area} \ \triangle ABM + {\rm Area} \ \triangle MCD \\ & = {\rm Area} \ \triangle AMD \left( 1 + \left( \frac{AM}{AD} \right)^2 + \left( \frac{MD}{AD} \right)^2 \right) \\ & = 6 \sqrt{5} . \end{align*}$

Therefore, the square of ${\rm Area} \ ABCD$ is $\left( 6 \sqrt{5} \right)^2 = \boxed{\textbf{(180) }}$ .

~Steven Chen (www.professorchenedu.com)

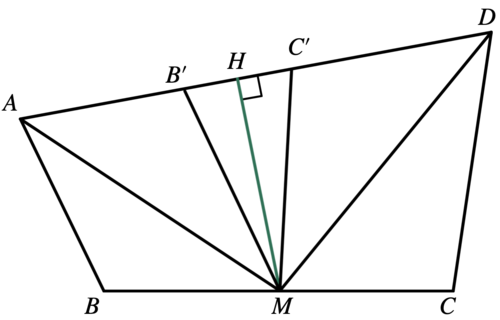
Solution 3 (Visual)

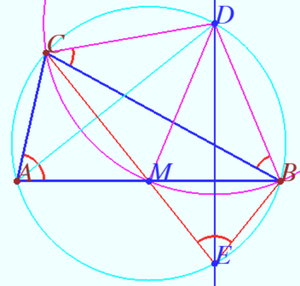
Lemma

In the triangle $ABC, AB = 2AC, M$ is the midpoint of $AB. D$ is the point of intersection of the circumscribed circle and the bisector of angle $A.$ Then $DM = BD.$

Proof

Let $A = 2\alpha.$ Then $\angle DBC = \angle DCB = \alpha.$

Let $E$ be the intersection point of the perpendicular dropped from $D$ to $AB$ with the circle.

Then the sum of arcs $\overset{\Large\frown} {BE} + \overset{\Large\frown}{AC} + \overset{\Large\frown}{CD} = \pi.$ $\overset{\Large\frown} {BE} = \pi – 2\alpha – \overset{\Large\frown}{AC}.$

Let $E'$ be the point of intersection of the line $CM$ with the circle. $CM$ is perpendicular to $AD, \angle AMC = \frac {\pi}{2} – \alpha,$ the sum of arcs $\overset{\Large\frown}{A}C + \overset{\Large\frown}{BE'} = \pi – 2\alpha,$ hence $E'$ coincides with $E.$

The inscribed angles $\angle DEM = \angle DEB, M$ is symmetric to $B$ with respect to $DE, DM = DB.$

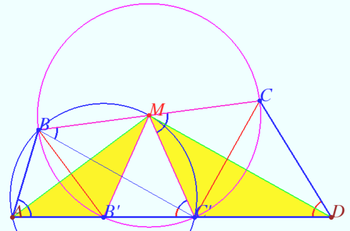
Solution

Let $AB' = AB, DC' = DC, B'$ and $C'$ on $AD.$ Then $AB' = 2, DC' = 3, B'C' = 2 = AB'.$

Quadrilateral $ABMC'$ is inscribed. Let $\angle A = 2\alpha.$ Then $\angle MBC' = \angle MC'B = \alpha.$

Circle $BB'C'C$ has center $M, BC$ is its diameter, $\angle BC'C = 90^o.$ $\angle DMC' = \angle MC'B,$ since they both complete $\angle MC'C$ to $90^o.$

$\angle MB'A = \angle MC'D,$ since they are the exterior angles of an isosceles $\triangle MB'C'.$ $\triangle AMB' \sim \triangle MDC'$ by two angles. $\frac {AB'}{MC'} = \frac {MB'}{DC'}, MC' =\sqrt{AB' \cdot C'D} = \sqrt{6}.$

The height dropped from $M$ to $AD$ is $\sqrt{MB'^2 - (\frac{B'C'}{2})^2} =\sqrt{6 - 1} = \sqrt{5}.$

The areas of triangles $\triangle AMB'$ and $\triangle MC'B'$ are equal to $\sqrt{5},$ area of $\triangle MC'D$ is $\frac{3}{2} \sqrt{5}.$

The areas of triangles $\triangle AMB'$ and $\triangle AMB$ as well as $\triangle MC'D$ and $\triangle MCD$ are equal.

The area of $ABCD$ is $(1 + 2 + 3) \sqrt{5} = 6\sqrt{5},$ its square is $\boxed{180}.$

Shelomovskii, vvsss, www.deoma-cmd.ru

@@ Line 130: / Line 130: @@
 The area of  <math>ABCD</math> is <math>(1 + 2 + 3) \sqrt{5} = 6\sqrt{5},</math> its square is <math>\boxed{180}.</math>
-~vvsss, www.deoma-cmd.ru
+'''Shelomovskii, vvsss,  www.deoma-cmd.ru'''
 ==See Also==
 {{AIME box|year=2022|n=II|num-b=10|num-a=12}}
 {{MAA Notice}}

2022 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 10	Followed by Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search