Difference between revisions of "2022 AIME II Problems/Problem 12"
m (→Solution) |
m |
||
| Line 31: | Line 31: | ||
~Steven Chen (www.professorchenedu.com) | ~Steven Chen (www.professorchenedu.com) | ||
| + | |||
| + | |||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/4qiu7GGUGIg | ||
| + | |||
| + | ~MathProblemSolvingSkills.com | ||
| + | |||
| + | |||
==See Also== | ==See Also== | ||
{{AIME box|year=2022|n=II|num-b=11|num-a=13}} | {{AIME box|year=2022|n=II|num-b=11|num-a=13}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 20:13, 10 January 2023
Contents
[hide]Problem
Let ![]() and
and ![]() be real numbers with
be real numbers with ![]() and
and ![]() such that
such that![]() Find the least possible value of
Find the least possible value of ![]()
Solution
Denote ![]()
![]() is an ellipse whose center is
is an ellipse whose center is ![]() and foci are
and foci are ![]() and
and ![]() .
. ![]() is an ellipse whose center is
is an ellipse whose center is ![]() and foci are
and foci are ![]() and
and ![]() .
.
Since ![]() is on
is on ![]() , the sum of distance from
, the sum of distance from ![]() to
to ![]() and
and ![]() is equal to twice the semi-major axis of this ellipse,
is equal to twice the semi-major axis of this ellipse, ![]() .
.
Since ![]() is on
is on ![]() , the sum of distance from
, the sum of distance from ![]() to
to ![]() and
and ![]() is equal to twice the semi-major axis of this ellipse,
is equal to twice the semi-major axis of this ellipse, ![]() .
.
Therefore, ![]() is the sum of the distance from
is the sum of the distance from ![]() to four foci of these two ellipses.
To minimize this,
to four foci of these two ellipses.
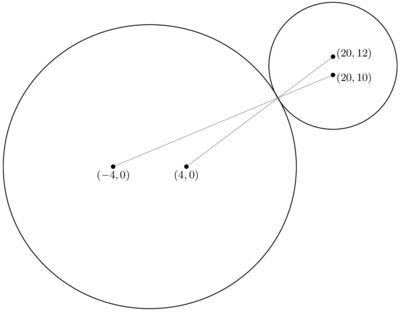
To minimize this, ![]() must be the intersection point of the line that passes through
must be the intersection point of the line that passes through ![]() and
and ![]() , and the line that passes through
, and the line that passes through ![]() and
and ![]() .
.
The distance between ![]() and
and ![]() is
is ![]() .
.
The distance between ![]() and
and ![]() is
is ![]() .
.
Hence, ![]() , i.e.
, i.e. ![]() .
.
The straight line connecting the points ![]() and
and ![]() has the equation
has the equation ![]() .
The straight line connecting the points
.
The straight line connecting the points ![]() and
and ![]() has the equation
has the equation ![]() .
These lines intersect at the point
.
These lines intersect at the point ![]() .
This point satisfies both equations for
.
This point satisfies both equations for ![]() .
Hence,
.
Hence, ![]() is possible.
is possible.
Therefore, ![]()
~Steven Chen (www.professorchenedu.com)
Video Solution
~MathProblemSolvingSkills.com
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.