Difference between revisions of "2019 AIME II Problems/Problem 7"

Revision as of 13:36, 4 January 2024

Problem

Triangle $ABC$ has side lengths $AB=120,BC=220$ , and $AC=180$ . Lines $\ell_A,\ell_B$ , and $\ell_C$ are drawn parallel to $\overline{BC},\overline{AC}$ , and $\overline{AB}$ , respectively, such that the intersections of $\ell_A,\ell_B$ , and $\ell_C$ with the interior of $\triangle ABC$ are segments of lengths $55,45$ , and $15$ , respectively. Find the perimeter of the triangle whose sides lie on lines $\ell_A,\ell_B$ , and $\ell_C$ .

Diagram

$[asy] /* Made by MRENTHUSIASM */ size(350); pair A, B, C, D, E, F, G, H, I, J, K, L; B = origin; C = (220,0); A = intersectionpoints(Circle(B,120),Circle(C,180))[0]; D = A+1/4*(B-A); E = A+1/4*(C-A); F = B+1/4*(A-B); G = B+1/4*(C-B); H = C+1/8*(A-C); I = C+1/8*(B-C); J = extension(D,E,F,G); K = extension(F,G,H,I); L = extension(H,I,D,E); draw(A--B--C--cycle); draw(J+9/8*(K-J)--K+9/8*(J-K),dashed); draw(L+9/8*(K-L)--K+9/8*(L-K),dashed); draw(J+9/8*(L-J)--L+9/8*(J-L),dashed); draw(D--E^^F--G^^H--I,red); dot("$B$",B,1.5SW,linewidth(4)); dot("$C$",C,1.5SE,linewidth(4)); dot("$A$",A,1.5N,linewidth(4)); dot(D,linewidth(4)); dot(E,linewidth(4)); dot(F,linewidth(4)); dot(G,linewidth(4)); dot(H,linewidth(4)); dot(I,linewidth(4)); dot(J,linewidth(4)); dot(K,linewidth(4)); dot(L,linewidth(4)); label("$55$",midpoint(D--E),S,red); label("$45$",midpoint(F--G),dir(55),red); label("$15$",midpoint(H--I),dir(160),red); label("$\ell_A$",J+9/8*(L-J),1.5*dir(B--C)); label("$\ell_B$",K+9/8*(J-K),1.5*dir(C--A)); label("$\ell_C$",L+9/8*(K-L),1.5*dir(A--B)); [/asy]$ ~MRENTHUSIASM

Solution 1

Let the points of intersection of $\ell_A, \ell_B,\ell_C$ with $\triangle ABC$ divide the sides into consecutive segments $BD,DE,EC,CF,FG,GA,AH,HI,IB$ . Furthermore, let the desired triangle be $\triangle XYZ$ , with $X$ closest to side $BC$ , $Y$ closest to side $AC$ , and $Z$ closest to side $AB$ . Hence, the desired perimeter is $XE+EF+FY+YG+GH+HZ+ZI+ID+DX=(DX+XE)+(FY+YG)+(HZ+ZI)+115$ since $HG=55$ , $EF=15$ , and $ID=45$ .

Note that $\triangle AHG\sim \triangle BID\sim \triangle EFC\sim \triangle ABC$ , so using similar triangle ratios, we find that $BI=HA=30$ , $BD=HG=55$ , $FC=\frac{45}{2}$ , and $EC=\frac{55}{2}$ .

We also notice that $\triangle EFC\sim \triangle YFG\sim \triangle EXD$ and $\triangle BID\sim \triangle HIZ$ . Using similar triangles, we get that $FY+YG=\frac{GF}{FC}\cdot \left(EF+EC\right)=\frac{225}{45}\cdot \left(15+\frac{55}{2}\right)=\frac{425}{2}$ $DX+XE=\frac{DE}{EC}\cdot \left(EF+FC\right)=\frac{275}{55}\cdot \left(15+\frac{45}{2}\right)=\frac{375}{2}$ $HZ+ZI=\frac{IH}{BI}\cdot \left(ID+BD\right)=2\cdot \left(45+55\right)=200$ Hence, the desired perimeter is $200+\frac{425+375}{2}+115=600+115=\boxed{715}$ -ktong

Solution 2

Let the diagram be set up like that in Solution 1.

By similar triangles we have $\frac{AH}{AB}=\frac{GH}{BC}\Longrightarrow AH=30$ $\frac{IB}{AB}=\frac{DI}{AC}\Longrightarrow IB=30$ Thus $HI=AB-AH-IB=60$

Since $\bigtriangleup IHZ\sim\bigtriangleup ABC$ and $\frac{HI}{AB}=\frac{1}{2}$ , the altitude of $\bigtriangleup IHZ$ from $Z$ is half the altitude of $\bigtriangleup ABC$ from $C$ , say $\frac{h}{2}$ . Also since $\frac{EF}{AB}=\frac{1}{8}$ , the distance from $\ell_C$ to $AB$ is $\frac{7}{8}h$ . Therefore the altitude of $\bigtriangleup XYZ$ from $Z$ is $\frac{1}{2}h+\frac{7}{8}h=\frac{11}{8}h$ .

By triangle scaling, the perimeter of $\bigtriangleup XYZ$ is $\frac{11}{8}$ of that of $\bigtriangleup ABC$ , or $\frac{11}{8}(220+180+120)=\boxed{715}$

~ Nafer

Solution 3

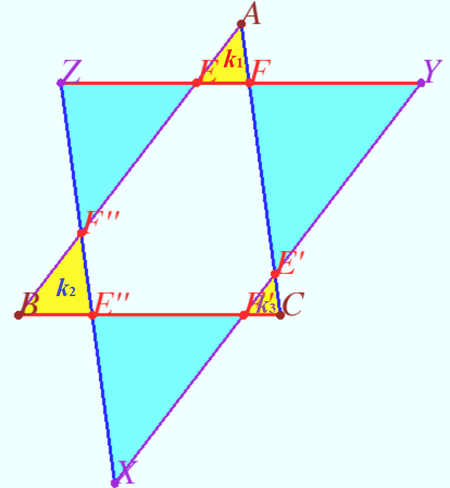
Notation shown on diagram. By similar triangles we have $k_1 = \frac{EF}{BC} = \frac{AE}{AB} = \frac {AF}{AC} = \frac {1}{4},$ $k_2 = \frac{F''E''}{AC} = \frac {BF''}{AB} = \frac{1}{4},$ $k_3 = \frac{E'F'}{AB} = \frac{E'C }{AC} = \frac{1}{8}.$ So, $\frac{ZE}{BC} = \frac{F''E}{AB} = \frac{AB - AE - BF''}{AB} = 1 - k_1 - k_2,$ $\frac{FY}{BC} = \frac{FE'}{AC} = \frac{AC - AF - CE'}{AC} = 1 - k_1 - k_3.$ $k = \frac{ZY}{BC} = \frac{ZE + EF + FY}{BC} = (1 - k_1 - k_2) + k_1 + (1 - k_1 - k_3)$ $k = 2 - k_1 - k_2 - k_3 = 2 - \frac{1}{4} - \frac{1}{4} - \frac{1}{8} = \frac{11}{8}.$ $\frac{ZY+YX +XZ}{BC +AB + AC} = k \implies ZY + YX + XZ =\frac{11}{8} (220 + 120 + 180) = \boxed {715}.$ vladimir.shelomovskii@gmail.com, vvsss

Solution 4 (Change of perspective)

$[asy] pair A,B,C; B = (0,0); C = (1,0); A = intersectionpoints(circle(B,3/2),circle(C,11/6))[0]; draw(A--B--C--cycle); draw((3/2,3/4)--(5/2,3/4)); draw((3/2,1/4)--(5/2,1/4)); draw((9/4,1)--(11/4,1/2)--(9/4,0)); draw(shift(dir(0)*15/4)*polygon(3)); [/asy]$

$[asy] for (int i=0; i<8; ++i) { for (int j=0; j<i+1; ++j) { draw(shift(dir(30))*shift(dir(0)*i*sqrt(3))*shift(dir(120)*j*sqrt(3))*polygon(3)); } } pair A = origin+2*sqrt(3)*dir(0)+7*sqrt(3)*dir(120); pair B = origin+13*sqrt(3)*dir(0)+7*sqrt(3)*dir(120); pair C = origin+2*sqrt(3)*dir(0)-4*sqrt(3)*dir(120); pair D = origin + 2*sqrt(3)*dir(0); pair E = origin + 2*sqrt(3)*dir(60); pair F = origin + 7*sqrt(3)*dir(60); pair G = origin + 7*sqrt(3)*dir(60) + 1*sqrt(3)*dir(0); pair H = origin + 6*sqrt(3)*dir(0) + 2*sqrt(3)*dir(60); pair I = origin + 6*sqrt(3)*dir(0); draw(A--B--C--cycle,linewidth(3)); draw(D--E,linewidth(3)+rgb(3/4,1/4,1/4)); draw(F--G,linewidth(3)+rgb(1/4,3/4,1/4)); draw(H--I,linewidth(3)+rgb(1/4,1/4,3/4)); [/asy]$

Let's squish a triangle with side lengths 15, 22.5, and 27.5 into a equilateral triangle with side length 1. Then, the original triangle gets turned into a equilateral triangle with side length 8. Since 15 is one eighth of 120, it has a length of one. Since 45 and 55 are one fourth of 180 and 220 respectively, they are both two long. We extend the three segments to form a big equilateral triangle shown in black. Notice it has a side length of 11. Now that our task is done, let's undo the distortion. We get 11(15+22.5+27.5)=11(65)=715.

2019 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 6	Followed by Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search