Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2012 AMC 8 Problems/Problem 5"

m
(→‎Solution: That wasn't even a solution before.)
Line 44: Line 44:
  
 
==Solution==
 
==Solution==
−
There is a segment of length one on the segment with length <math> 6 </math>, which creates a segment of length <math> 5 </math>, which is also the value of <math> X </math>. Thus, the answer is <math> \boxed{\textbf{(E)}\ 5} </math>.
+
[[File:2012amc85.png]]
 +
The figure is the same height on both sides, so the sum of the lengths contributing to the height on the left side will equal the sum of the lengths contributing to the height on the left side.
 +
 
 +
<math>1 + 1 + 1 + 2 + X = 1 + 2 + 1 + 6\\
 +
5 + X = 10\\
 +
X = 5</math>
 +
 
 +
Thus, the answer is <math> \boxed{\textbf{(E)}\ 5} </math>.
  
 
==See Also==
 
==See Also==
 
{{AMC8 box|year=2012|num-b=4|num-a=6}}
 
{{AMC8 box|year=2012|num-b=4|num-a=6}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Revision as of 10:17, 23 November 2013

Problem

In the diagram, all angles are right angles and the lengths of the sides are given in centimeters. Note the diagram is not drawn to scale. What is , $X$ in centimeters?

[asy] pair A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R; A=(4,0); B=(7,0); C=(7,4); D=(8,4); E=(8,5); F=(10,5); G=(10,7); H=(7,7); I=(7,8); J=(5,8); K=(5,7); L=(4,7); M=(4,6); N=(0,6); O=(0,5); P=(2,5); Q=(2,3); R=(4,3); draw(A--B--C--D--E--F--G--H--I--J--K--L--M--N--O--P--Q--R--cycle); label("$X$",(3.4,1.5)); label("6",(7.6,1.5)); label("1",(7.6,3.5)); label("1",(8.4,4.6)); label("2",(9.4,4.6)); label("2",(10.4,6)); label("3",(8.4,7.4)); label("1",(7.5,7.8)); label("2",(6,8.5)); label("1",(4.7,7.8)); label("1",(4.3,7.5)); label("1",(3.5,6.5)); label("4",(1.8,6.5)); label("1",(-0.5,5.5)); label("2",(0.8,4.5)); label("2",(1.5,3.8)); label("2",(2.8,2.6));[/asy]

$\textbf{(A)}\hspace{.05in}1\qquad\textbf{(B)}\hspace{.05in}2\qquad\textbf{(C)}\hspace{.05in}3\qquad\textbf{(D)}\hspace{.05in}4\qquad\textbf{(E)}\hspace{.05in}5$

Solution

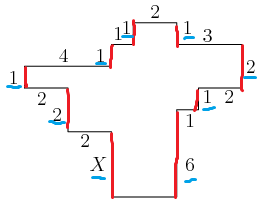2012amc85.png The figure is the same height on both sides, so the sum of the lengths contributing to the height on the left side will equal the sum of the lengths contributing to the height on the left side.

$1 + 1 + 1 + 2 + X = 1 + 2 + 1 + 6\\ 5 + X = 10\\ X = 5$

Thus, the answer is $\boxed{\textbf{(E)}\ 5}$.

See Also

2012 AMC 8 (Problems • Answer Key • Resources)
Preceded by
Problem 4 		Followed by
Problem 6
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2012_AMC_8_Problems/Problem_5&oldid=57877"