2006 AIME I Problems/Problem 6
Problem
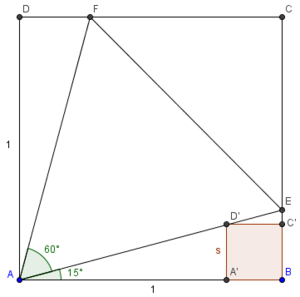
Square ![]() has sides of length 1. Points
has sides of length 1. Points ![]() and
and ![]() are on
are on ![]() and
and ![]() respectively, so that
respectively, so that ![]() is equilateral. A square with vertex
is equilateral. A square with vertex ![]() has sides that are parallel to those of
has sides that are parallel to those of ![]() and a vertex on
and a vertex on ![]() The length of a side of this smaller square is
The length of a side of this smaller square is ![]() where
where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
Solution
Call the vertices of the new square A', B', C', and D', in relation to the vertices of ![]() , and define
, and define ![]() to be one of the sides of that square. Since the sides are parallel, by corresponding angles and AA~ we know that triangles
to be one of the sides of that square. Since the sides are parallel, by corresponding angles and AA~ we know that triangles ![]() and
and ![]() are similar. Thus, the sides are proportional:
are similar. Thus, the sides are proportional: ![]() . Simplifying, we get that
. Simplifying, we get that ![]() .
.
![]() is
is ![]() degrees, so
degrees, so ![]() . Thus,
. Thus, ![]() , so
, so ![]() . Since
. Since ![]() is equilateral,
is equilateral, ![]() .
. ![]() is a
is a ![]() , so
, so ![]() . Substituting back into the equation from the beginning, we get
. Substituting back into the equation from the beginning, we get ![]() , so
, so ![]() . Therefore,
. Therefore, ![]() , and
, and ![]() .
.
Here's an alternative geometric way to calculate ![]() (as opposed to trigonometric): The diagonal
(as opposed to trigonometric): The diagonal ![]() is made of the altitude of the equilateral triangle and the altitude of the
is made of the altitude of the equilateral triangle and the altitude of the ![]() . The former is
. The former is ![]() , and the latter is
, and the latter is ![]() ; thus
; thus ![]() . The solution continues as above.
. The solution continues as above.
See also
| 2006 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||