2022 AIME II Problems/Problem 11
Problem
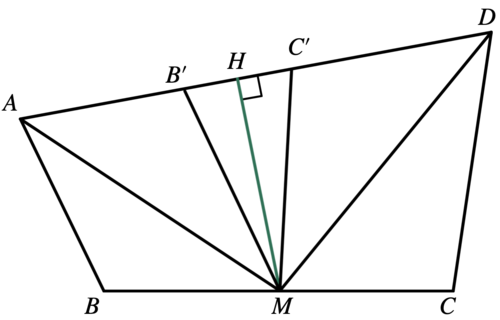
Let ![]() be a convex quadrilateral with
be a convex quadrilateral with ![]() ,
, ![]() , and
, and ![]() such that the bisectors of acute angles
such that the bisectors of acute angles ![]() and
and ![]() intersect at the midpoint of
intersect at the midpoint of ![]() . Find the square of the area of
. Find the square of the area of ![]() .
.
Solution
According to the problem, we have ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
Because ![]() is the midpoint of
is the midpoint of ![]() , we have
, we have ![]() , so:
, so: ![]()
Then, we can see that ![]() is an isosceles triangle with
is an isosceles triangle with ![]()
Therefore, we could start our angle chasing: ![]() .
.
This is when we found that points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are on a circle. Thus,
are on a circle. Thus, ![]() . This is the time we found that
. This is the time we found that ![]() .
.
Thus, ![]()
Point ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() .
. ![]() .
.
The area of this quadrilateral is the sum of areas of triangles: ![]()
![]()
![]()
![]()
Finally, the square of the area is ![]()
~DSAERF-CALMIT
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.