2005 AMC 10A Problems/Problem 23
Problem
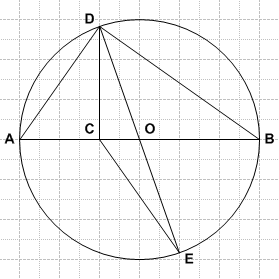
Let ![]() be a diameter of a circle and let
be a diameter of a circle and let ![]() be a point on
be a point on ![]() with
with ![]() . Let
. Let ![]() and
and ![]() be points on the circle such that
be points on the circle such that ![]() and
and ![]() is a second diameter. What is the ratio of the area of
is a second diameter. What is the ratio of the area of ![]() to the area of
to the area of ![]() ?
?
![]()
Solution 1
Let us assume that the diameter is of length ![]() .
.
![]() is
is ![]() of diameter and
of diameter and ![]() is
is ![]() .
.
![]() is the radius of the circle, so using the Pythagorean theorem height
is the radius of the circle, so using the Pythagorean theorem height ![]() of
of ![]() is
is ![]() . This is also the height of the
. This is also the height of the ![]() .
.
Area of the ![]() is
is ![]() =
= ![]() .
.
The height of ![]() can be found using the area of
can be found using the area of ![]() and
and ![]() as base.
as base.
Hence the height of ![]() is
is ![]() =
= ![]() .
.
The diameter is the base for both the triangles ![]() and
and ![]() .
.
Hence, the ratio of the area of ![]() to the area of
to the area of ![]() is
is
![]() =
= ![]()
Solution 2
Since ![]() and
and ![]() share a base, the ratio of their areas is the ratio of their altitudes. Draw the altitude from
share a base, the ratio of their areas is the ratio of their altitudes. Draw the altitude from ![]() to
to ![]() .
.
![[asy] import graph; import olympiad; pair O,A,B,C,D,E,F; O=(0,0);A=(15,0);B=(-15,0);C=(5,0);D=(5,14.142135623730950488016887242097);E=(-5,-14.142135623730950488016887242097);F=(0.5555555555555555,1.5713484026367722764463208046774); draw(Circle((0,0),15)); draw(A--B);draw(D--E);draw(C--D);draw(C--E);draw(C--F);draw(A--D);draw(D--B); label("A",A,NE);label("B",B,W);label("C",C,SE);label("D",D,NE);label("E",E,SW);label("O",O,SW);label("F",F,NW); markscalefactor=0.2; draw(anglemark(C,F,D),blue);draw(anglemark(D,C,B),blue); [/asy]](http://latex.artofproblemsolving.com/5/e/9/5e9629039a8bbef0413de3c19a864acbdb600acc.png)
![]() .
.
Since ![]() , then
, then ![]() . So the ratio of the two altitudes is
. So the ratio of the two altitudes is ![]()
Solution 3
Say the center of the circle is point F;
Without loss of generality, assume ![]() , so
, so ![]() and the diameter and radius are
and the diameter and radius are ![]() and
and ![]() , respectively. Therefore,
, respectively. Therefore, ![]() and
and ![]() .
The area of
.
The area of ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() is the radius of circle
is the radius of circle ![]() .
. ![]() happens to be the area of
happens to be the area of ![]() . Furthermore,
. Furthermore, ![]() or
or ![]() Therefore, the ratio is
Therefore, the ratio is ![]()
See also
| 2005 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.