2022 AIME II Problems/Problem 11
Contents
Problem
Let ![]() be a convex quadrilateral with
be a convex quadrilateral with ![]() ,
, ![]() , and
, and ![]() such that the bisectors of acute angles
such that the bisectors of acute angles ![]() and
and ![]() intersect at the midpoint of
intersect at the midpoint of ![]() . Find the square of the area of
. Find the square of the area of ![]() .
.
Solution 1
According to the problem, we have ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
Because ![]() is the midpoint of
is the midpoint of ![]() , we have
, we have ![]() , so:
, so: ![]()
Then, we can see that ![]() is an isosceles triangle with
is an isosceles triangle with ![]()
Therefore, we could start our angle chasing: ![]() .
.
This is when we found that points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are on a circle. Thus,
are on a circle. Thus, ![]() . This is the time we found that
. This is the time we found that ![]() .
.
Thus, ![]()
Point ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() .
. ![]() .
.
The area of this quadrilateral is the sum of areas of triangles: ![]()
![]()
![]()
![]()
Finally, the square of the area is ![]()
~DSAERF-CALMIT (https://binaryphi.site)
Solution 2
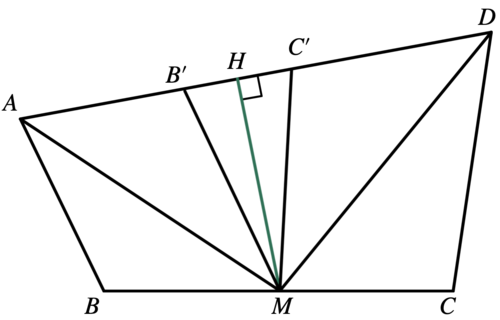
Denote by ![]() the midpoint of segment
the midpoint of segment ![]() .
Let points
.
Let points ![]() and
and ![]() be on segment
be on segment ![]() , such that
, such that ![]() and
and ![]() .
.
Denote ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Denote ![]() . Because
. Because ![]() is the midpoint of
is the midpoint of ![]() ,
, ![]() .
.
Because ![]() is the angle bisector of
is the angle bisector of ![]() and
and ![]() ,
, ![]() .
Hence,
.
Hence, ![]() and
and ![]() .
Hence,
.
Hence, ![]() .
.
Because ![]() is the angle bisector of
is the angle bisector of ![]() and
and ![]() ,
, ![]() .
Hence,
.
Hence, ![]() and
and ![]() .
Hence,
.
Hence, ![]() .
.
Because ![]() is the midpoint of segment
is the midpoint of segment ![]() ,
, ![]() .
Because
.
Because ![]() and
and ![]() ,
, ![]() .
Thus,
.
Thus, ![]() .
Thus,
\[
\alpha + \theta = \beta + \phi . \hspace{1cm} (1)
\]
.
Thus,
\[
\alpha + \theta = \beta + \phi . \hspace{1cm} (1)
\]
In ![]() ,
, ![]() .
In addition,
.
In addition, ![]() .
Thus,
\[
\alpha + \beta = \theta + \phi . \hspace{1cm} (2)
\]
.
Thus,
\[
\alpha + \beta = \theta + \phi . \hspace{1cm} (2)
\]
Taking ![]() , we get
, we get ![]() .
Taking
.
Taking ![]() , we get
, we get ![]() .
.
Therefore, ![]() .
.
Hence, ![]() and
and ![]() .
Thus,
.
Thus, ![]() and
and ![]() .
.
In ![]() , by applying the law of cosines,
, by applying the law of cosines, ![]() .
Hence,
.
Hence, ![]() .
Hence,
.
Hence, ![]() .
.
Therefore, \begin{align*} {\rm Area} \ ABCD & = {\rm Area} \ \triangle AMD + {\rm Area} \ \triangle ABM + {\rm Area} \ \triangle MCD \\ & = {\rm Area} \ \triangle AMD \left( 1 + \left( \frac{AM}{AD} \right)^2 + \left( \frac{MD}{AD} \right)^2 \right) \\ & = 6 \sqrt{5} . \end{align*}
Therefore, the square of ![]() is
is ![]() .
.
~Steven Chen (www.professorchenedu.com)
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.