Euler line
In any triangle ![]() , the Euler line is a line which passes through the orthocenter
, the Euler line is a line which passes through the orthocenter ![]() , centroid
, centroid ![]() , circumcenter
, circumcenter ![]() , nine-point center
, nine-point center ![]() and de Longchamps point
and de Longchamps point ![]() . It is named after Leonhard Euler. Its existence is a non-trivial fact of Euclidean geometry. Certain fixed orders and distance ratios hold among these points. In particular,
. It is named after Leonhard Euler. Its existence is a non-trivial fact of Euclidean geometry. Certain fixed orders and distance ratios hold among these points. In particular, ![]() and
and ![]()
Euler line is the central line ![]() .
.
Given the orthic triangle ![]() of
of ![]() , the Euler lines of
, the Euler lines of ![]() ,
,![]() , and
, and ![]() concur at
concur at ![]() , the nine-point circle of
, the nine-point circle of ![]() .
.
Contents
[hide]Proof Centroid Lies on Euler Line
This proof utilizes the concept of spiral similarity, which in this case is a rotation followed homothety. Consider the medial triangle ![]() . It is similar to
. It is similar to ![]() . Specifically, a rotation of
. Specifically, a rotation of ![]() about the midpoint of
about the midpoint of ![]() followed by a homothety with scale factor
followed by a homothety with scale factor ![]() centered at
centered at ![]() brings
brings ![]() . Let us examine what else this transformation, which we denote as
. Let us examine what else this transformation, which we denote as ![]() , will do.
, will do.
It turns out ![]() is the orthocenter, and
is the orthocenter, and ![]() is the centroid of
is the centroid of ![]() . Thus,
. Thus, ![]() . As a homothety preserves angles, it follows that
. As a homothety preserves angles, it follows that ![]() . Finally, as
. Finally, as ![]() it follows that
it follows that
![]() Thus,
Thus, ![]() are collinear, and
are collinear, and ![]() .
.
Another Proof
Let ![]() be the midpoint of
be the midpoint of ![]() .
Extend
.
Extend ![]() past
past ![]() to point
to point ![]() such that
such that ![]() . We will show
. We will show ![]() is the orthocenter.
Consider triangles
is the orthocenter.
Consider triangles ![]() and
and ![]() . Since
. Since ![]() , and they both share a vertical angle, they are similar by SAS similarity. Thus,
, and they both share a vertical angle, they are similar by SAS similarity. Thus, ![]() , so
, so ![]() lies on the
lies on the ![]() altitude of
altitude of ![]() . We can analogously show that
. We can analogously show that ![]() also lies on the
also lies on the ![]() and
and ![]() altitudes, so
altitudes, so ![]() is the orthocenter.
is the orthocenter.
Proof Nine-Point Center Lies on Euler Line
Assuming that the nine point circle exists and that ![]() is the center, note that a homothety centered at
is the center, note that a homothety centered at ![]() with factor
with factor ![]() brings the Euler points
brings the Euler points ![]() onto the circumcircle of
onto the circumcircle of ![]() . Thus, it brings the nine-point circle to the circumcircle. Additionally,
. Thus, it brings the nine-point circle to the circumcircle. Additionally, ![]() should be sent to
should be sent to ![]() , thus
, thus ![]() and
and ![]() .
.
Analytic Proof of Existence
Let the circumcenter be represented by the vector ![]() , and let vectors
, and let vectors ![]() correspond to the vertices of the triangle. It is well known the that the orthocenter is
correspond to the vertices of the triangle. It is well known the that the orthocenter is ![]() and the centroid is
and the centroid is ![]() . Thus,
. Thus, ![]() are collinear and
are collinear and ![]()
Triangles with angles of  or
or 
Claim 1
Let the ![]() in triangle
in triangle ![]() be
be ![]() Then the Euler line of the
Then the Euler line of the ![]() is parallel to the bisector of
is parallel to the bisector of ![]()
Proof
Let ![]() be circumcircle of
be circumcircle of ![]()
Let ![]() be circumcenter of
be circumcenter of ![]()
Let ![]() be the circle symmetric to
be the circle symmetric to ![]() with respect to
with respect to ![]()
Let ![]() be the point symmetric to
be the point symmetric to ![]() with respect to
with respect to ![]()
The ![]() lies on
lies on ![]() lies on
lies on ![]()
![]() is the radius of
is the radius of ![]() and
and ![]() translation vector
translation vector ![]() to
to ![]() is
is ![]()
Let ![]() be the point symmetric to
be the point symmetric to ![]() with respect to
with respect to ![]() Well known that
Well known that ![]() lies on
lies on ![]() Therefore point
Therefore point ![]() lies on
lies on ![]()
Point ![]() lies on
lies on ![]()
Let ![]() be the bisector of
be the bisector of ![]() are concurrent.
are concurrent.
![]()
Euler line ![]() of the
of the ![]() is parallel to the bisector
is parallel to the bisector ![]() of
of ![]() as desired.
as desired.
Claim 2
Let the ![]() in triangle
in triangle ![]() be
be ![]() Then the Euler line of the
Then the Euler line of the ![]() is perpendicular to the bisector of
is perpendicular to the bisector of ![]()
Proof
Let ![]() be circumcircle, circumcenter, orthocenter and incenter of the
be circumcircle, circumcenter, orthocenter and incenter of the ![]()
![]()
![]()
![]() points
points ![]() are concyclic.
are concyclic.
The circle ![]() centered at midpoint of small arc
centered at midpoint of small arc ![]()
![]() is rhomb.
is rhomb.
Therefore the Euler line ![]() is perpendicular to
is perpendicular to ![]() as desired.
as desired.
Claim 3
Let ![]() be a quadrilateral whose diagonals
be a quadrilateral whose diagonals ![]() and
and ![]() intersect at
intersect at ![]() and form an angle of
and form an angle of ![]() If the triangles PAB, PBC, PCD, PDA are all not equilateral, then their Euler lines are pairwise parallel or coincident.
If the triangles PAB, PBC, PCD, PDA are all not equilateral, then their Euler lines are pairwise parallel or coincident.
Proof
Let ![]() and
and ![]() be internal and external bisectors of the angle
be internal and external bisectors of the angle ![]() .
.
Then Euler lines of ![]() and
and ![]() are parallel to
are parallel to ![]() and Euler lines of
and Euler lines of ![]() and
and ![]() are perpendicular to
are perpendicular to ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
Concurrent Euler lines and Fermat points
Consider a triangle ![]() with Fermat–Torricelli points
with Fermat–Torricelli points ![]() and
and ![]() The Euler lines of the
The Euler lines of the ![]() triangles with vertices chosen from
triangles with vertices chosen from ![]() and
and ![]() are concurrent at the centroid
are concurrent at the centroid ![]() of triangle
of triangle ![]() We denote centroids by
We denote centroids by ![]() , circumcenters by
, circumcenters by ![]() We use red color for points and lines of triangles
We use red color for points and lines of triangles ![]() green color for triangles
green color for triangles ![]() and blue color for triangles
and blue color for triangles ![]()
Case 1
Let ![]() be the first Fermat point of
be the first Fermat point of ![]() maximum angle of which smaller then
maximum angle of which smaller then ![]() Then the centroid of triangle
Then the centroid of triangle ![]() lies on Euler line of the
lies on Euler line of the ![]() The pairwise angles between these Euler lines are equal
The pairwise angles between these Euler lines are equal ![]()
Proof
Let ![]() and
and ![]() be centroid, circumcenter, and circumcircle of
be centroid, circumcenter, and circumcircle of ![]() respectevely.
respectevely.
Let ![]() be external for
be external for ![]() equilateral triangle
equilateral triangle ![]()
![]() is cyclic.
is cyclic.
Point ![]() is centroid of
is centroid of ![]()
![]()
![]()
![]() Points
Points ![]() and
and ![]() are colinear, so point
are colinear, so point ![]() lies on Euler line
lies on Euler line ![]() of
of ![]()
![]()
Case 2
Let ![]() be the first Fermat point of
be the first Fermat point of ![]()
Then the centroid ![]() of triangle
of triangle ![]() lies on Euler lines of the triangles
lies on Euler lines of the triangles ![]() and
and ![]() The pairwise angles between these Euler lines are equal
The pairwise angles between these Euler lines are equal ![]()
Proof
Let ![]() be external for
be external for ![]() equilateral triangle,
equilateral triangle, ![]() be circumcircle of
be circumcircle of ![]()
![]() is cyclic.
is cyclic.
Point ![]() is centroid of
is centroid of ![]()
![]()
Points ![]() and
and ![]() are colinear, so point
are colinear, so point ![]() lies on Euler line
lies on Euler line ![]() of
of ![]() as desired.
as desired.
Case 3
Let ![]() be the second Fermat point of
be the second Fermat point of ![]() Then the centroid
Then the centroid ![]() of triangle
of triangle ![]() lies on Euler lines of the triangles
lies on Euler lines of the triangles ![]() and
and ![]()
The pairwise angles between these Euler lines are equal ![]()
Proof
Let ![]() be internal for
be internal for ![]() equilateral triangle,
equilateral triangle, ![]() be circumcircle of
be circumcircle of ![]()
Let ![]() and
and ![]() be circumcenters of the triangles
be circumcenters of the triangles ![]() and
and ![]() Point
Point ![]() is centroid of the
is centroid of the ![]() is the Euler line of the
is the Euler line of the ![]() parallel to
parallel to ![]()
![]() is bisector of
is bisector of ![]() is bisector of
is bisector of ![]() is bisector of
is bisector of ![]() is regular triangle.
is regular triangle.
![]() is the inner Napoleon triangle of the
is the inner Napoleon triangle of the ![]() is centroid of this regular triangle.
is centroid of this regular triangle.
![]()
![]() points
points ![]() and
and ![]() are collinear as desired.
are collinear as desired.
Similarly, points ![]() and
and ![]() are collinear.
are collinear.
Case 4
Let ![]() and
and ![]() be the Fermat points of
be the Fermat points of ![]() Then the centroid of
Then the centroid of ![]() point
point ![]() lies on Euler line
lies on Euler line ![]() is circumcenter,
is circumcenter, ![]() is centroid) of the
is centroid) of the ![]()
Proof
Step 1 We will find line ![]() which is parallel to
which is parallel to ![]()
Let ![]() be midpoint of
be midpoint of ![]() Let
Let ![]() be the midpoint of
be the midpoint of ![]()
Let ![]() be point symmetrical to
be point symmetrical to ![]() with respect to
with respect to ![]()
![]() as midline of
as midline of ![]()
![]()
![]()
Step 2 We will prove that line ![]() is parallel to
is parallel to ![]()
Let ![]() be the inner Napoleon triangle. Let
be the inner Napoleon triangle. Let ![]() be the outer Napoleon triangle. These triangles are regular centered at
be the outer Napoleon triangle. These triangles are regular centered at ![]()
Points ![]() and
and ![]() are collinear (they lies on bisector
are collinear (they lies on bisector ![]()
Points ![]() and
and ![]() are collinear (they lies on bisector
are collinear (they lies on bisector ![]()
Points ![]() and
and ![]() are collinear (they lies on bisector
are collinear (they lies on bisector ![]()
![]()
![]()
![]() angle between
angle between ![]() and
and ![]() is
is ![]()
![]()
Points ![]() and
and ![]() are concyclic
are concyclic ![]()
![]() Points
Points ![]() and
and ![]() are concyclic
are concyclic ![]()
![]() points
points ![]() and
and ![]() are concyclic
are concyclic
![]()
![]() Therefore
Therefore ![]() and
and ![]() are collinear or point
are collinear or point ![]() lies on Euler line
lies on Euler line ![]()
vladimir.shelomovskii@gmail.com, vvsss
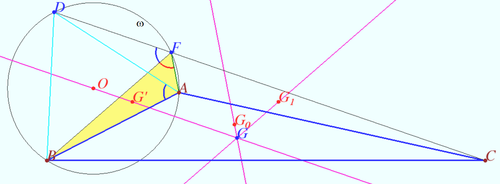
Euler line of Gergonne triangle
Prove that the Euler line of Gergonne triangle of ![]() passes through the circumcenter of triangle
passes through the circumcenter of triangle ![]()
Gergonne triangle is also known as the contact triangle or intouch triangle. If the inscribed circle touches the sides of ![]() at points
at points ![]() and
and ![]() then
then ![]() is Gergonne triangle of
is Gergonne triangle of ![]() .
.
Other wording: Tangents to circumcircle of ![]() are drawn at the vertices of the triangle. Prove that the circumcenter of the triangle formed by these three tangents lies on the Euler line of the original triangle.
are drawn at the vertices of the triangle. Prove that the circumcenter of the triangle formed by these three tangents lies on the Euler line of the original triangle.
Proof
Let ![]() and
and ![]() be orthocenter and circumcenter of
be orthocenter and circumcenter of ![]() respectively.
Let
respectively.
Let ![]() be Orthic Triangle of
be Orthic Triangle of ![]()
Then ![]() is Euler line of
is Euler line of ![]()
![]() is the incenter of
is the incenter of ![]()
![]() is the incenter of
is the incenter of ![]()
![]()
Similarly, ![]()
![]() where
where ![]() is the perspector of triangles
is the perspector of triangles ![]() and
and ![]()
Under homothety with center P and coefficient ![]() the incenter
the incenter ![]() of
of ![]() maps into incenter
maps into incenter ![]() of
of ![]() , circumcenter
, circumcenter ![]() of
of ![]() maps into circumcenter
maps into circumcenter ![]() of
of ![]() are collinear as desired.
are collinear as desired.
vladimir.shelomovskii@gmail.com, vvsss
Thebault point
Let ![]() and
and ![]() be the altitudes of the
be the altitudes of the ![]() where
where ![]()
a) Prove that the Euler lines of triangles ![]() are concurrent on the nine-point circle at a point T (Thebault point of
are concurrent on the nine-point circle at a point T (Thebault point of ![]() )
)
b) Prove that if ![]() then
then ![]() else
else ![]()
Proof
Case 1 Acute triangle
a) It is known, that Euler line of acute triangle ![]() cross AB and BC (shortest and longest sides) in inner points.
cross AB and BC (shortest and longest sides) in inner points.
Let ![]() be circumcenters of
be circumcenters of ![]()
Let ![]() and
and ![]() be centroids of
be centroids of ![]()
Denote ![]() is the circle
is the circle ![]() (the nine-points circle).
(the nine-points circle).
![]() is the midpoint
is the midpoint ![]() where
where ![]() is the orthocenter of
is the orthocenter of ![]()
Similarly ![]()
![]() is the midline of
is the midline of ![]()
Let ![]() cross
cross ![]() at point
at point ![]() different from
different from ![]()
![]() spiral similarity centered at
spiral similarity centered at ![]() maps
maps ![]() onto
onto ![]()
This similarity has the rotation angle ![]() acute angle between Euler lines of these triangles is
acute angle between Euler lines of these triangles is ![]()
Let these lines crossed at point ![]() Therefore
Therefore ![]() points
points ![]() and
and ![]() are concyclic
are concyclic ![]()
Similarly, ![]() as desired.
as desired.
b) ![]() Point
Point ![]() lies on median of
lies on median of ![]() and divide it in ratio 2 : 1.
and divide it in ratio 2 : 1.
Point ![]() lies on Euler line of
lies on Euler line of ![]()
According the Claim, ![]()
![]()
Similarly ![]()
Case 2 Obtuse triangle
a) It is known, that Euler line of obtuse ![]() cross AC and BC (middle and longest sides) in inner points.
cross AC and BC (middle and longest sides) in inner points.
Let ![]() be circumcenters of
be circumcenters of ![]()
Let ![]() and
and ![]() be centroids of
be centroids of ![]()
Denote ![]()
![]() is the circle
is the circle ![]() (the nine-points circle).
(the nine-points circle).
![]() is the midpoint
is the midpoint ![]() where
where ![]() is the orthocenter of
is the orthocenter of ![]()
Similarly ![]()
![]() is the midline of
is the midline of ![]()
Let ![]() cross
cross ![]() at point
at point ![]() different from
different from ![]()
![]() spiral similarity centered at
spiral similarity centered at ![]() maps
maps ![]() onto
onto ![]()
This similarity has the rotation angle ![]() acute angle between Euler lines of these triangles is
acute angle between Euler lines of these triangles is ![]()
Let these lines crossed at point ![]() Therefore
Therefore ![]() points
points ![]() and
and ![]() are concyclic
are concyclic ![]()
Similarly, ![]() as desired.
as desired.
b) ![]()
![]()
Point ![]() lies on median of
lies on median of ![]() and divide it in ratio
and divide it in ratio ![]()
Point ![]() lies on Euler line of
lies on Euler line of ![]() According the Claim,
According the Claim, ![]()
![]()
Similarly ![]()
Claim (Segment crossing the median)
Let ![]() be the midpoint of side
be the midpoint of side ![]() of the
of the ![]()
![]()
Then ![]()
Proof
Let ![]() be
be ![]() (We use sign
(We use sign ![]() to denote the area of
to denote the area of ![]()
Denote ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Schiffler point
Let ![]() and
and ![]() be the incenter, circumcenter, centroid, circumradius,
be the incenter, circumcenter, centroid, circumradius, ![]() and inradius of
and inradius of ![]() respectively. Then the Euler lines of the four triangles
respectively. Then the Euler lines of the four triangles ![]() and
and ![]() are concurrent at Schiffler point
are concurrent at Schiffler point ![]() .
.
Proof
We will prove that the Euler line ![]() of
of ![]() cross the Euler line
cross the Euler line ![]() of
of ![]() at such point
at such point ![]() that
that ![]() .
.
Let ![]() and
and ![]() be the circumcenter and centroid of
be the circumcenter and centroid of ![]() respectively.
respectively.
It is known that ![]() lies on circumcircle of
lies on circumcircle of ![]()
Denote ![]()
It is known that ![]() is midpoint
is midpoint ![]() point
point ![]() lies on median
lies on median ![]() points
points ![]() belong the bisector of
belong the bisector of ![]()
Easy to find that ![]() ,
,
![]()
We use sigh [t] for area of t. We get
![]()
![]()
![]() Using Claim we get
Using Claim we get
![]() Therefore each Euler line of triangles
Therefore each Euler line of triangles ![]() cross Euler line of
cross Euler line of ![]() in the same point, as desired.
in the same point, as desired.
Claim (Segments crossing inside triangle)
Given triangle GOY. Point ![]() lies on
lies on ![]()
Point ![]() lies on
lies on ![]()
Point ![]() lies on
lies on ![]()
Point ![]() lies on
lies on ![]() Then
Then ![]()
Proof
Let ![]() be
be ![]() (We use sigh
(We use sigh ![]() for area of
for area of ![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
See also
This article is a stub. Help us out by expanding it.