2011 AMC 12A Problems/Problem 6

Problem

The players on a basketball team made some three-point shots, some two-point shots, and some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team's total score was $61$ points. How many free throws did they make?

$\textbf{(A)}\ 13 \qquad \textbf{(B)}\ 14 \qquad \textbf{(C)}\ 15 \qquad \textbf{(D)}\ 16 \qquad \textbf{(E)}\ 17$

Solution 1

For the points made from two-point shots and from three-point shots to be equal, the numbers of made shots are in a $3:2$ ratio. Therefore, assume they made $3x$ and $2x$ two- and three- point shots, respectively, and thus $3x+1$ free throws. The total number of points is $2 \times (3x) + 3 \times (2x) + 1 \times (3x+1) = 15x+1$

Set that equal to $61$ , we get $x = 4$ , and therefore the number of free throws they made $3 \times 4 + 1 = 13 \Rightarrow \boxed{A}$

Solution 2

Let $x$ be the number of free throws. Then the number of points scored by two-pointers is $2(x-1)$ and the same goes for three-pointers because they scored the same number of points with twos and threes. Thus, our equation is $x+4(x-1) = 61 \Rightarrow x=13$ , giving us $\boxed{(A)}$ for an answer.

Solution 3

We let $a$ be the number of $2$ -point shots, $b$ be the number of $3$ -point shots, and $x$ be the number of free throws. We are looking for $x.$ We know that $2a=3b,$ and that $x=a+1.$ We know that $2a+3b+1x=61.$ We can see: 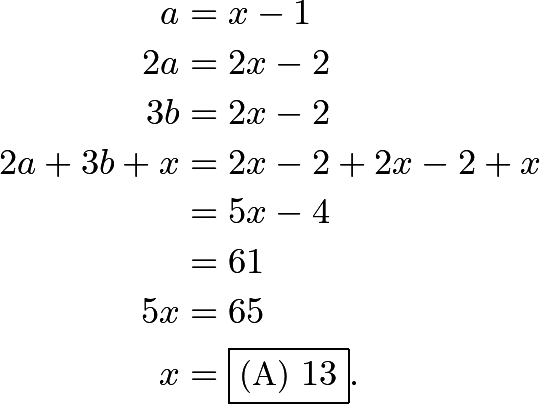~Technodoggo

Video Solution

https://www.youtube.com/watch?v=6tlqpAcmbz4 ~Shreyas S

2011 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 5	Followed by Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

2011 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 11	Followed by Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.

Page

Toolbox

Search