2005 AMC 10A Problems/Problem 20

Problem

An equilangular octagon has four sides of length $1$ and four sides of length $\frac{\sqrt{2}}{2}$ , arranged so that no two consecutive sides have the same length. What is the area of the octagon?

$\textbf{(A) } \frac72\qquad \textbf{(B) } \frac{7\sqrt2}{2}\qquad \textbf{(C) } \frac{5+4\sqrt2}{2}\qquad \textbf{(D) } \frac{4+5\sqrt2}{2}\qquad \textbf{(E) } 7$

Solution 1

The area of the octagon can be divided up into $5$ squares with side $\frac{\sqrt2}2$ and $4$ right triangles, which are half the area of each of the squares.

Therefore, the area of the octagon is equal to the area of $5+4\left(\frac12\right)=7$ squares.

The area of each square is $\left(\frac{\sqrt2}2\right)^2=\frac12$ , so the area of $7$ squares is $\boxed{\textbf{(A) }\frac72}$ .

$[asy] pair A=(0.5, 0), B=(0, 0.5), C=(0, 1.5), D=(0.5, 2), E=(1.5, 2), F=(2, 1.5), G=(2, 0.5), H=(1.5, 0); draw(A--B); draw(B--C); draw(C--D); draw(D--E);draw(E--F);draw(F--G); draw(G--H); draw(H--A);draw(A--F, blue);draw(E--B,blue);draw(C--H, blue); draw(D--G,blue);dot(A);dot(B);dot(C);dot(D);dot(E);dot(F);dot(G);dot(H); [/asy]$

Solution 2

Using the diagram from above, we can extend the sides of length $1$ to form four right triangles and the octagon, all inside a square. If you wanted, you could also extend the sides of length $\frac{\sqrt{2}}{2}$ and get the same answer, but that would make things slightly harder. The right triangles are $45-45-90$ triangles with hypotenuse $\frac{\sqrt{2}}{2}$ , so the side length is $\frac{1}{2}$ . Thus, the area of the larger square is $2 \cdot 2 = 4$ , and the area of the four right triangles combined is $\frac{1}{2}$ , so the area of the octagon is $4-\frac{1}{2}=\boxed{\textbf{(A) }\frac{7}{2}}$

edited by mobius247

Solution 3

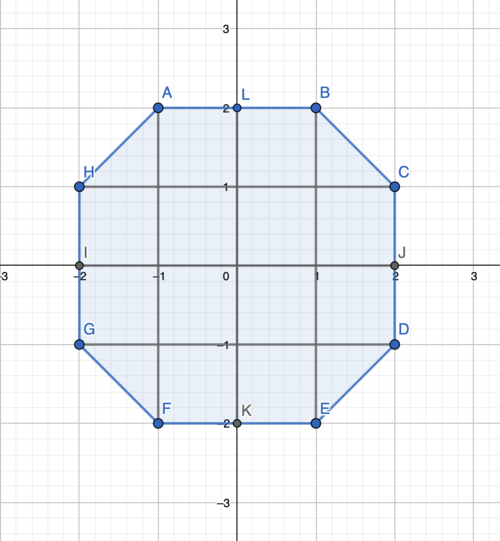
Refer to the following diagram:

(Picture made on Geogebra)

Note that each square has area $\frac14$ , and each triangle has area $\frac18$ . The total area is $12\cdot\frac14+4\cdot\frac18=\frac72 \Longrightarrow \boxed{\textbf{(A) } \frac72}$ .

Remark: This solution requires careful drawing, and also realising that connecting lines leads to squares and isosceles right triangles (notice the $\sqrt{2}$ and realise that it is the hypotenuse of a $45-45-90$ triangle with side length ratios $1:1:\sqrt{2}$ .).

~JH. L

Video Solution

CHECK OUT Video Solution: https://youtu.be/rwPFZnYk9V8

2005 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 19	Followed by Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search