1983 AHSME Problems/Problem 17
Problem
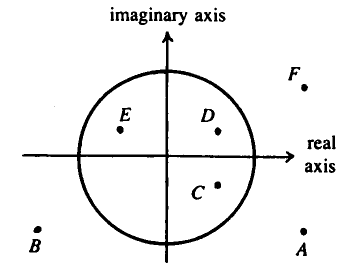
The diagram above shows several numbers in the complex plane. The circle is the unit circle centered at the origin.
One of these numbers is the reciprocal of ![]() . Which one?
. Which one?
![]()
Solution
Write ![]() as
as ![]() , where we see from the diagram that
, where we see from the diagram that ![]() and
and ![]() (as
(as ![]() is outside the unit circle). We have
is outside the unit circle). We have ![]() , so, since
, so, since ![]() , the reciprocal of
, the reciprocal of ![]() has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of
has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of ![]() 's magnitude (since
's magnitude (since ![]() ); as
); as ![]() 's magnitude is greater than
's magnitude is greater than ![]() , its reciprocal's magnitude will thus be between
, its reciprocal's magnitude will thus be between ![]() and
and ![]() , so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of
, so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of ![]() is point
is point ![]() .
.
See Also
| 1983 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 16 |
Followed by Problem 18 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.