Difference between revisions of "1983 AHSME Problems/Problem 4"
(Created page with "<asy> pair A, B, C, D, E, F; A = (0, 1.732); B = (0.5, 0.866); C = (0,0); D = (1, 0); E = (1.5, 0.866); F = (1, 1.732); draw(A--B--C--D--E--F--A); label("A", A, dir(point--A))...") |
(→See Also) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | == Problem 4 == | ||
| + | |||
| + | [[File:pdfresizer.com-pdf-convert.png]] | ||
| + | |||
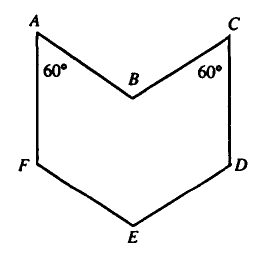
| + | In the adjoining plane figure, sides <math>AF</math> and <math>CD</math> are parallel, as are sides <math>AB</math> and <math>EF</math>, | ||
| + | and sides <math>BC</math> and <math>ED</math>. Each side has length <math>1</math>. Also, <math>\angle FAB = \angle BCD = 60^\circ</math>. | ||
| + | The area of the figure is | ||
| + | |||
| + | <math> | ||
| + | \textbf{(A)} \ \frac{\sqrt 3}{2} \qquad | ||
| + | \textbf{(B)} \ 1 \qquad | ||
| + | \textbf{(C)} \ \frac{3}{2} \qquad | ||
| + | \textbf{(D)}\ \sqrt{3}\qquad | ||
| + | \textbf{(E)}\ 2</math> | ||
| + | |||
| + | [[1983 AHSME Problems/Problem 4|Solution]] | ||
| + | |||
| + | ==Solution== | ||
<asy> | <asy> | ||
pair A, B, C, D, E, F; | pair A, B, C, D, E, F; | ||
| Line 8: | Line 26: | ||
F = (1, 1.732); | F = (1, 1.732); | ||
draw(A--B--C--D--E--F--A); | draw(A--B--C--D--E--F--A); | ||
| − | label("A", A, | + | label("$A$", A, NW); |
| + | label("$B$", B, 3W); | ||
| + | label("$C$", C, SW); | ||
| + | label("$D$", D, SE); | ||
| + | label("$E$", E, E); | ||
| + | label("$F$", F, NE); | ||
| + | draw(B--D, dashed+linewidth(0.5)); | ||
| + | draw(B--E, dashed+linewidth(0.5)); | ||
| + | draw(B--F, dashed+linewidth(0.5)); | ||
</asy> | </asy> | ||
| + | |||
| + | By rotating the diagram and drawing the dotted lines, we see that the figure can be divided into four equilateral triangles, each of side length <math>1</math>. The area of one such equilateral triangle is <math>\frac{\sqrt{3}}{4} \cdot 1^2 = \frac{\sqrt{3}}{4}</math>, which gives a total of <math>4\left(\frac{\sqrt{3}}{4}\right) = \sqrt{3}</math>, or <math>\boxed{D}</math>. | ||
| + | |||
| + | ==See Also== | ||
| + | {{AHSME box|year=1983|num-b=3|num-a=5}} | ||
| + | |||
| + | {{MAA Notice}} | ||
| + | |||
| + | [[Category: Introductory Geometry Problems]] | ||
Latest revision as of 06:36, 27 January 2019
Problem 4
In the adjoining plane figure, sides 
and 
are parallel, as are sides 
and 
,
and sides 
and 
. Each side has length 
. Also, 
.
The area of the figure is
Solution
![[asy] pair A, B, C, D, E, F; A = (0, 1.732); B = (0.5, 0.866); C = (0,0); D = (1, 0); E = (1.5, 0.866); F = (1, 1.732); draw(A--B--C--D--E--F--A); label("$A$", A, NW); label("$B$", B, 3W); label("$C$", C, SW); label("$D$", D, SE); label("$E$", E, E); label("$F$", F, NE); draw(B--D, dashed+linewidth(0.5)); draw(B--E, dashed+linewidth(0.5)); draw(B--F, dashed+linewidth(0.5)); [/asy]](http://latex.artofproblemsolving.com/b/d/d/bddb9e658c2a3f38841b9348a1aa73ffaeadbc5e.png)
By rotating the diagram and drawing the dotted lines, we see that the figure can be divided into four equilateral triangles, each of side length . The area of one such equilateral triangle is 
, which gives a total of 
, or 
.
See Also
| 1983 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
