1985 AIME Problems/Problem 15
Problem
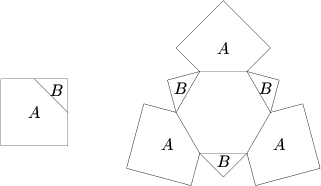
Three 12 cm ![]() 12 cm squares are each cut into two pieces
12 cm squares are each cut into two pieces ![]() and
and ![]() , as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in
, as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in ![]() ) of this polyhedron?
) of this polyhedron?
Solution 1 (For the visualizers)
Note that gluing two of the given polyhedra together along a hexagonal face (rotated ![]() from each other) yields a cube, so the volume is
from each other) yields a cube, so the volume is ![]() , so our answer is
, so our answer is ![]() .
.
Solution 2
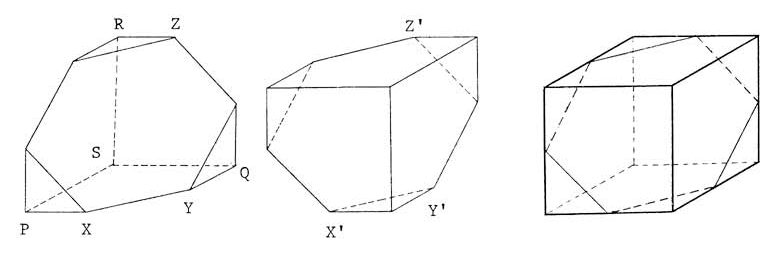
Taking a reference to the above left diagram, obviously SP, SQ and SR are perpendicular to each other. Thus expanding plane SPQ, SQR and SRP to intersect with the plane XYZ that contains the regular hexagon, we form a pyramid with S the top vertex and the base being an equilateral triangle with side length of 18 ![]() . This pyramid has a volume of 972, because it is also 1/6 of the volume of a cube with side length of 18. Then subtracting 3 congruent pyramids with volume of 36 each, we get
. This pyramid has a volume of 972, because it is also 1/6 of the volume of a cube with side length of 18. Then subtracting 3 congruent pyramids with volume of 36 each, we get ![]() .
.
Solution 3
Position the polyhedra with the facing hexagon down. From this perspective it is clear that the polyhedra can be thought of as a tetrahedron with 3 smaller tetrahedra removed from each of the three corners of its base. The strategy is then to calculate the volume of the larger tetrahedron, and then subtract the three smaller ones.
Focusing on the larger tetrahedron, the base is an equilateral triangle formed by extending the sides of the base hexagon; this triangle has sides of length ![]() . Thus its area is
. Thus its area is ![]() .
The height of the tetrahedron can be calculated by considering the following right triangle: Leg 1 is the height of the tetrahedron (which we seek); Leg 2 is the distance from a midpoint of one of the sides of the base to the base's center; and the Hypotenuse is the distance from the midpoint of one of the sides of the base to the top vertex. Leg 2 has a length of
.
The height of the tetrahedron can be calculated by considering the following right triangle: Leg 1 is the height of the tetrahedron (which we seek); Leg 2 is the distance from a midpoint of one of the sides of the base to the base's center; and the Hypotenuse is the distance from the midpoint of one of the sides of the base to the top vertex. Leg 2 has a length of ![]() . And the hypotenuse's length is
. And the hypotenuse's length is ![]() (each non-base face of the tetrahedron is an isosceles right triangle with leg of length 18, whose altitude to its hypotenuse has length
(each non-base face of the tetrahedron is an isosceles right triangle with leg of length 18, whose altitude to its hypotenuse has length ![]() ). Thus, by the Pythagorean theorem the height of the tetrahedron is
). Thus, by the Pythagorean theorem the height of the tetrahedron is ![]() . Altogether, the Volume of the large tetrahedron is
. Altogether, the Volume of the large tetrahedron is ![]() .
.
Lastly, each smaller tetrahedron removed from a corner of the base of the larger one has sides whose lengths are ![]() that of the larger tetrahedron. Since volume scales with the cube of length, each of these tetrahedra are
that of the larger tetrahedron. Since volume scales with the cube of length, each of these tetrahedra are ![]() the volume of the larger one. There are three of them so the final volume is
the volume of the larger one. There are three of them so the final volume is ![]() .
.
See also
| 1985 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||