Difference between revisions of "1985 AIME Problems/Problem 15"
Mathcool2009 (talk | contribs) (→Solution) |
Mathgeek2006 (talk | contribs) m (→Solution) |
||
| Line 7: | Line 7: | ||
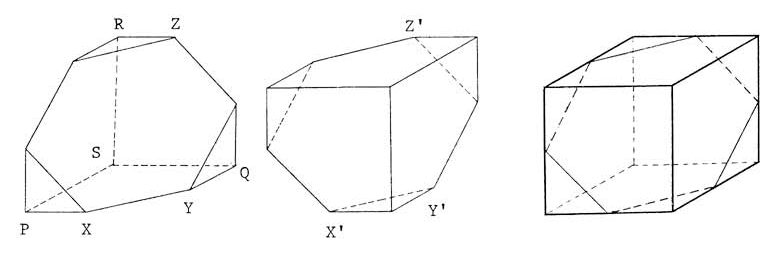
Note that gluing two of the given polyhedra together along a hexagonal face (rotated <math>60^\circ</math> from each other) yields a [[cube (geometry) | cube]], so the volume is <math>\frac12 \cdot 12^3 = 864</math>. | Note that gluing two of the given polyhedra together along a hexagonal face (rotated <math>60^\circ</math> from each other) yields a [[cube (geometry) | cube]], so the volume is <math>\frac12 \cdot 12^3 = 864</math>. | ||
| − | Image: [[ | + | Image: [[Image:AoPS_AIME_1985.png]] |
== See also == | == See also == | ||
Revision as of 15:41, 13 March 2015
Problem
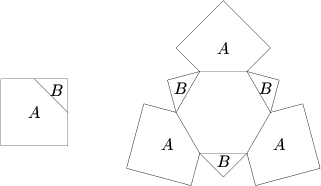
Three 12 cm ![]() 12 cm squares are each cut into two pieces
12 cm squares are each cut into two pieces ![]() and
and ![]() , as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in
, as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in ![]() ) of this polyhedron?
) of this polyhedron?
Solution
Note that gluing two of the given polyhedra together along a hexagonal face (rotated ![]() from each other) yields a cube, so the volume is
from each other) yields a cube, so the volume is ![]() .
.
See also
| 1985 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||