1997 AIME Problems/Problem 4
Contents
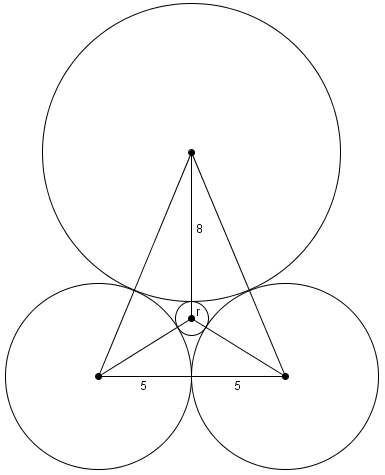
Problem
Circles of radii ![]() and
and ![]() are mutually externally tangent, where
are mutually externally tangent, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Solution
If (in the diagram above) we draw the line going through the centers of the circles with radii ![]() and
and ![]() , that line is the perpendicular bisector of the segment connecting the centers of the two circles with radii
, that line is the perpendicular bisector of the segment connecting the centers of the two circles with radii ![]() . Then we form two right triangles, of lengths
. Then we form two right triangles, of lengths ![]() and
and ![]() , wher
, wher ![]() is the distance between the center of the circle in question and the segment connecting the centers of the two circles of radii
is the distance between the center of the circle in question and the segment connecting the centers of the two circles of radii ![]() . By the Pythagorean Theorem, we now have two equations with two unknowns:
. By the Pythagorean Theorem, we now have two equations with two unknowns:

So ![]() .
.
NOTE: It can be seen that there is no apparent need to use the variable x as a 5,12,13 right triangle has been formed.
Solution 2
We may also use Descartes' theorem, ![]() where each of
where each of ![]() is the curvature of a circle with radius
is the curvature of a circle with radius ![]() , and the curvature is defined as
, and the curvature is defined as ![]() . The larger solution for
. The larger solution for ![]() will give the curvature of the circle externally tangent to the other circles, while the smaller solution will give the curvature for the circle internally tangent to each of the other circles. Using Descartes' theorem, we get
will give the curvature of the circle externally tangent to the other circles, while the smaller solution will give the curvature for the circle internally tangent to each of the other circles. Using Descartes' theorem, we get ![]() . Thus,
. Thus, ![]() , and the answer is
, and the answer is ![]()
See also
| 1997 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.