1997 AIME Problems/Problem 6
Problem
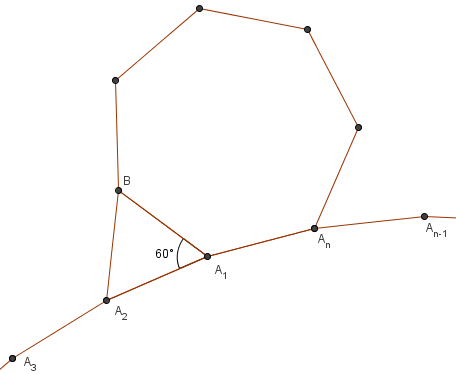
Point ![]() is in the exterior of the regular
is in the exterior of the regular ![]() -sided polygon
-sided polygon ![]() , and
, and ![]() is an equilateral triangle. What is the largest value of
is an equilateral triangle. What is the largest value of ![]() for which
for which ![]() ,
, ![]() , and
, and ![]() are consecutive vertices of a regular polygon?
are consecutive vertices of a regular polygon?
Solution 1
Let the other regular polygon have ![]() sides. Using the interior angle of a regular polygon formula, we have
sides. Using the interior angle of a regular polygon formula, we have ![]() ,
, ![]() , and
, and ![]() . Since those three angles add up to
. Since those three angles add up to ![]() ,
,
 Using SFFT,
Using SFFT,
![]() Clearly
Clearly ![]() is maximized when
is maximized when ![]() .
.
Solution 2
As above, find that ![]() using the formula for the interior angle of a polygon.
using the formula for the interior angle of a polygon.
Solve for ![]() to find that
to find that ![]() . Clearly,
. Clearly, ![]() for
for ![]() to be positive.
to be positive.
With this restriction of ![]() , the larger
, the larger ![]() gets, the smaller the fraction
gets, the smaller the fraction ![]() becomes. This can be proven either by calculus, by noting that
becomes. This can be proven either by calculus, by noting that ![]() is a transformed hyperbola, or by dividing out the rational function to get
is a transformed hyperbola, or by dividing out the rational function to get ![]()
Either way, minimizng ![]() will maximize
will maximize ![]() , and the smallest integer
, and the smallest integer ![]() such that
such that ![]() is positive is
is positive is ![]() , giving
, giving ![]()
Solution 3
From the formula for the measure for an individual angle of a regular n-gon, ![]() , the measure of
, the measure of ![]() . Together with the fact that an equilateral triangle has angles measuring 60 degrees, the measure of
. Together with the fact that an equilateral triangle has angles measuring 60 degrees, the measure of ![]() (Notice that this value decreases as
(Notice that this value decreases as ![]() increases; hence, we are looking for the least possible value of
increases; hence, we are looking for the least possible value of ![]() ). For
). For ![]() to be vertices of a regular polygon,
to be vertices of a regular polygon, ![]() must be of the form
must be of the form ![]() , where
, where ![]() is a natural number greater than or equal to 3. It is obvious that
is a natural number greater than or equal to 3. It is obvious that ![]() . The least angle satisfying this condition is
. The least angle satisfying this condition is ![]() . Equating this with
. Equating this with ![]() and solving yields
and solving yields ![]()
See also
| 1997 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||