2002 AMC 12A Problems
| 2002 AMC 12A (Answer Key) Printable versions: • AoPS Resources • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
Contents
- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
Compute the sum of all the roots of
![]()
![]()
Problem 2
Cindy was asked by her teacher to subtract 3 from a certain number and then divide the result by 9. Instead, she subtracted 9 and then divided the result by 3, giving an answer of 43. What would her answer have been had she worked the problem correctly?
![]()
Problem 3
According to the standard convention for exponentiation,
![]()
If the order in which the exponentiations are performed is changed, how many other values are possible?
![]()
Problem 4
Find the degree measure of an angle whose complement is 25% of its supplement.
![]()
Problem 5
Each of the small circles in the figure has radius one. The innermost circle is tangent to the six circles that surround it, and each of those circles is tangent to the large circle and to its small-circle neighbors. Find the area of the shaded region.
![[asy] import graph; unitsize(.3cm); path c=Circle((0,2),1); filldraw(Circle((0,0),3),grey,black); filldraw(Circle((0,0),1),white,black); filldraw(c,white,black); filldraw(rotate(60)*c,white,black); filldraw(rotate(120)*c,white,black); filldraw(rotate(180)*c,white,black); filldraw(rotate(240)*c,white,black); filldraw(rotate(300)*c,white,black); [/asy]](http://latex.artofproblemsolving.com/e/f/2/ef247dc86b9efff9368a791035527f5c512d1db8.png)
![]()
Problem 6
For how many positive integers ![]() does there exist at least one positive integer
does there exist at least one positive integer ![]() such that
such that ![]() ?
?
![]() infinitely many
infinitely many
Problem 7
A ![]() arc of circle A is equal in length to a
arc of circle A is equal in length to a ![]() arc of circle B. What is the ratio of circle A's area and circle B's area?
arc of circle B. What is the ratio of circle A's area and circle B's area?
![]()
Problem 8
Betsy designed a flag using blue triangles, small white squares, and a red center square, as shown. Let ![]() be the total area of the blue triangles,
be the total area of the blue triangles, ![]() the total area of the white squares, and
the total area of the white squares, and ![]() the area of the red square. Which of the following is correct?
the area of the red square. Which of the following is correct?
![[asy] unitsize(3mm); fill((-4,-4)--(-4,4)--(4,4)--(4,-4)--cycle,blue); fill((-2,-2)--(-2,2)--(2,2)--(2,-2)--cycle,red); path onewhite=(-3,3)--(-2,4)--(-1,3)--(-2,2)--(-3,3)--(-1,3)--(0,4)--(1,3)--(0,2)--(-1,3)--(1,3)--(2,4)--(3,3)--(2,2)--(1,3)--cycle; path divider=(-2,2)--(-3,3)--cycle; fill(onewhite,white); fill(rotate(90)*onewhite,white); fill(rotate(180)*onewhite,white); fill(rotate(270)*onewhite,white); [/asy]](http://latex.artofproblemsolving.com/a/0/b/a0b90bdab50e7b1984850bd644f9291ddc2de34e.png)
![]()
Problem 9
Jamal wants to save 30 files onto disks, each with 1.44 MB space. 3 of the files take up 0.8 MB, 12 of the files take up 0.7 MB, and the rest take up 0.4 MB. It is not possible to split a file onto 2 different disks. What is the smallest number of disks needed to store all 30 files?
![]()
Problem 10
Sarah places four ounces of coffee into an eight-ounce cup and four ounces of cream into a second cup of the same size. She then pours half the coffee from the first cup to the second and, after stirring thoroughly, pours half the liquid in the second cup back to the first. What fraction of the liquid in the first cup is now cream?
![]()
Problem 11
Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he drives at an average speed of 40 miles per hour, he will be late by 3 minutes. If he drives at an average speed of 60 miles per hour, he will be early by 3 minutes. How many miles per hour does Mr. Bird need to drive to get to work exactly on time?
![]()
Problem 12
Both roots of the quadratic equation ![]() are prime numbers. The number of possible values of
are prime numbers. The number of possible values of ![]() is
is
![]()
Problem 13
Two different positive numbers ![]() and
and ![]() each differ from their reciprocals by
each differ from their reciprocals by ![]() . What is
. What is ![]() ?
?
![]()
Problem 14
For all positive integers ![]() , let
, let ![]() . Let
. Let ![]() . Which of the following relations is true?
. Which of the following relations is true?
![]()
Problem 15
The mean, median, unique mode, and range of a collection of eight integers are all equal to 8. The largest integer that can be an element of this collection is
![]()
Problem 16
Tina randomly selects two distinct numbers from the set ![]() , and Sergio randomly selects a number from the set
, and Sergio randomly selects a number from the set ![]() . What is the probability that Sergio's number is larger than the sum of the two numbers chosen by Tina?
. What is the probability that Sergio's number is larger than the sum of the two numbers chosen by Tina?
![]()
Problem 17
Several sets of prime numbers, such as ![]() use each of the nine nonzero digits exactly once. What is the smallest possible sum such a set of primes could have?
use each of the nine nonzero digits exactly once. What is the smallest possible sum such a set of primes could have?
![]()
Problem 18
Let ![]() and
and ![]() be circles defined by
be circles defined by ![]() and
and ![]() respectively. What is the length of the shortest line segment
respectively. What is the length of the shortest line segment ![]() that is tangent to
that is tangent to ![]() at
at ![]() and to
and to ![]() at
at ![]() ?
?
![]()
Problem 19
The graph of the function ![]() is shown below. How many solutions does the equation
is shown below. How many solutions does the equation ![]() have?
have?
![[asy] import graph; size(200); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=4; pair P1=(-7,-4), P2=(-2,6), P3=(0,0), P4=(1,6), P5=(5,-6); real[] xticks={-7,-6,-5,-4,-3,-2,-1,1,2,3,4,5,6}; real[] yticks={-6,-5,-4,-3,-2,-1,1,2,3,4,5,6}; draw(P1--P2--P3--P4--P5); dot("(-7, -4)",P1); dot("(-2, 6)",P2,LeftSide); dot("(1, 6)",P4); dot("(5, -6)",P5); xaxis("$x$",-7.5,7,Ticks(xticks),EndArrow(6)); yaxis("$y$",-6.5,7,Ticks(yticks),EndArrow(6)); [/asy]](http://latex.artofproblemsolving.com/3/6/2/362b0483980187e4b1323e15d697b44643a97cf5.png)
![]()
Problem 20
Suppose that ![]() and
and ![]() are digits, not both nine and not both zero, and the repeating decimal
are digits, not both nine and not both zero, and the repeating decimal ![]() is expressed as a fraction in lowest terms. How many different denominators are possible?
is expressed as a fraction in lowest terms. How many different denominators are possible?
![]()
Problem 21
Consider the sequence of numbers: ![]() For
For ![]() , the
, the ![]() -th term of the sequence is the units digit of the sum of the two previous terms. Let
-th term of the sequence is the units digit of the sum of the two previous terms. Let ![]() denote the sum of the first
denote the sum of the first ![]() terms of this sequence. The smallest value of
terms of this sequence. The smallest value of ![]() for which
for which ![]() is:
is:
![]()
Problem 22
Triangle ![]() is a right triangle with
is a right triangle with ![]() as its right angle,
as its right angle, ![]() , and
, and ![]() . Let
. Let ![]() be randomly chosen inside
be randomly chosen inside ![]() , and extend
, and extend ![]() to meet
to meet ![]() at
at ![]() . What is the probability that
. What is the probability that ![]() ?
?
![]()
Problem 23
In triangle ![]() , side
, side ![]() and the perpendicular bisector of
and the perpendicular bisector of ![]() meet in point
meet in point ![]() , and
, and ![]() bisects
bisects ![]() . If
. If ![]() and
and ![]() , what is the area of triangle
, what is the area of triangle ![]() ?
?
![]()
Problem 24
Find the number of ordered pairs of real numbers ![]() such that
such that ![]() .
.
![]()
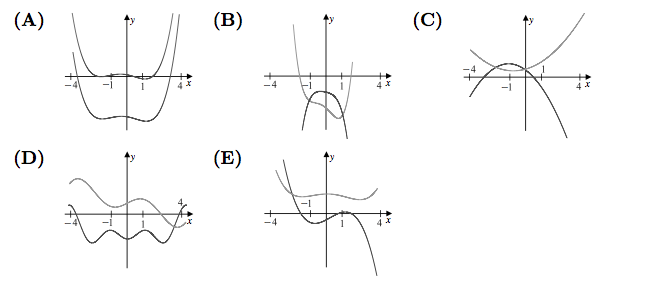
Problem 25
The nonzero coefficients of a polynomial ![]() with real coefficients are all replaced by their mean to form a polynomial
with real coefficients are all replaced by their mean to form a polynomial ![]() . Which of the following could be a graph of
. Which of the following could be a graph of ![]() and
and ![]() over the interval
over the interval ![]() ?
?
See also
| 2002 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by 2001 AMC 12 Problems |
Followed by 2002 AMC 12B Problems |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.