Difference between revisions of "2005 AMC 10A Problems"
Brut3Forc3 (talk | contribs) m (→Problem 1) |
Brut3Forc3 (talk | contribs) (→Problem 5) |
||
| Line 32: | Line 32: | ||
== Problem 5 == | == Problem 5 == | ||
| − | A store normally sells windows at <math> | + | A store normally sells windows at <math>\</math>100<math> each. This week the store is offering one free window for each purchase of four. Dave needs seven windows and Doug needs eight windows. How many dollars will they save if they purchase the windows together rather than separately? |
| − | <math> \mathrm{(A) \ } 100\qquad \mathrm{(B) \ } 200\qquad \mathrm{(C) \ } 300\qquad \mathrm{(D) \ } 400\qquad \mathrm{(E) \ } 500 | + | </math> \mathrm{(A) \ } 100\qquad \mathrm{(B) \ } 200\qquad \mathrm{(C) \ } 300\qquad \mathrm{(D) \ } 400\qquad \mathrm{(E) \ } 500 $ |
[[2005 AMC 10A Problems/Problem 5|Solution]] | [[2005 AMC 10A Problems/Problem 5|Solution]] | ||
Revision as of 02:00, 15 January 2008
Contents
- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
While eating out, Mike and Joe each tipped their server ![]() dollars. Mike tipped
dollars. Mike tipped ![]() of his bill and Joe tipped
of his bill and Joe tipped ![]() of his bill. What was the difference, in dollars between their bills?
of his bill. What was the difference, in dollars between their bills?
![]()
Problem 2
For each pair of real numbers ![]()
![]()
![]() , define the operation
, define the operation ![]() as
as
![]() .
.
What is the value of ![]() ?
?
![]()
Problem 3
The equations ![]() and
and ![]() have the same solution
have the same solution ![]() . What is the value of
. What is the value of ![]() ?
?
![]()
Problem 4
A rectangle with a diagonal of length ![]() is twice as long as it is wide. What is the area of the rectangle?
is twice as long as it is wide. What is the area of the rectangle?
![]()
Problem 5
A store normally sells windows at ![]() 100
100![]() \mathrm{(A) \ } 100\qquad \mathrm{(B) \ } 200\qquad \mathrm{(C) \ } 300\qquad \mathrm{(D) \ } 400\qquad \mathrm{(E) \ } 500 $
\mathrm{(A) \ } 100\qquad \mathrm{(B) \ } 200\qquad \mathrm{(C) \ } 300\qquad \mathrm{(D) \ } 400\qquad \mathrm{(E) \ } 500 $
Problem 6
The average (mean) of ![]() numbers is
numbers is ![]() , and the average of
, and the average of ![]() other numbers is
other numbers is ![]() . What is the average of all
. What is the average of all ![]() numbers?
numbers?
![]()
Problem 7
Josh and Mike live ![]() miles apart. Yesterday Josh started to ride his bicycle toward Mike's house. A little later Mike started to ride his bicycle toward Josh's house. When they met, Josh had ridden for twice the length of time as Mike and at four-fifths of Mike's rate. How many miles had Mike ridden when they met?
miles apart. Yesterday Josh started to ride his bicycle toward Mike's house. A little later Mike started to ride his bicycle toward Josh's house. When they met, Josh had ridden for twice the length of time as Mike and at four-fifths of Mike's rate. How many miles had Mike ridden when they met?
![]()
Problem 8
Problem 9
Three tiles are marked ![]() and two other tiles are marked
and two other tiles are marked ![]() . The five tiles are randomly arranged in a row. What is the probability that the arrangement reads
. The five tiles are randomly arranged in a row. What is the probability that the arrangement reads ![]() ?
?
![]()
Problem 10
There are two values of ![]() for which the equation
for which the equation ![]() has only one solution for
has only one solution for ![]() . What is the sum of those values of
. What is the sum of those values of ![]() ?
?
![]()
Problem 11
A wooden cube ![]() units on a side is painted red on all six faces and then cut into
units on a side is painted red on all six faces and then cut into ![]() unit cubes. Exactly one-fourth of the total number of faces of the unit cubes are red. What is
unit cubes. Exactly one-fourth of the total number of faces of the unit cubes are red. What is ![]() ?
?
![]()
Problem 12
The figure shown is called a trefoil and is constructed by drawing circular sectors about the sides of the congruent equilateral triangles. What is the area of a trefoil whose horizontal base has length ![]() ?
?
![]()
Problem 13
How many positive integers ![]() satisfy the following condition:
satisfy the following condition:
![]() ?
?
![]()
Problem 14
How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?
![]()
Problem 15
How many positive cubes divide ![]() ?
?
![]()
Problem 16
The sum of the digits of a two-digit number is subtracted from the number. The units digit of the result is ![]() . How many two-digit numbers have this property?
. How many two-digit numbers have this property?
![]()
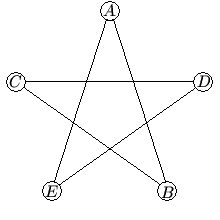
Problem 17
In the five-sided star shown, the letters ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are replaced by the numbers
are replaced by the numbers ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , although not necessarily in this order. The sums of the numbers at the ends of the line segments
, although not necessarily in this order. The sums of the numbers at the ends of the line segments ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() form an arithmetic sequence, although not necessarily in this order. What is the middle term of the sequence?
form an arithmetic sequence, although not necessarily in this order. What is the middle term of the sequence?
![]()
Problem 18
Team A and team B play a series. The first team to win three games wins the series. Each team is equally likely to win each game, there are no ties, and the outcomes of the individual games are independent. If team B wins the second game and team A wins the series, what is the probability that team B wins the first game?
![]()
Problem 19
Problem 20
An equiangular octagon has four sides of length 1 and four sides of length ![]() , arranged so that no two consecutive sides have the same length. What is the area of the octagon?
, arranged so that no two consecutive sides have the same length. What is the area of the octagon?
![]()
Problem 21
For how many positive integers ![]() does
does ![]() evenly divide
evenly divide ![]() ?
?
![]()
Problem 22
Let ![]() be the set of the
be the set of the ![]() smallest positive multiples of
smallest positive multiples of ![]() , and let
, and let ![]() be the set of the
be the set of the ![]() smallest positive multiples of
smallest positive multiples of ![]() . How many elements are common to
. How many elements are common to ![]() and
and ![]() ?
?
![]()
Problem 23
![]() is a square. Point
is a square. Point ![]() is chosen outside of
is chosen outside of ![]() such that angle
such that angle ![]() and
and ![]() . Point
. Point ![]() is chosen inside
is chosen inside ![]() such that the triangles
such that the triangles ![]() and
and ![]() are congruent. If
are congruent. If ![]() , compute the area of
, compute the area of ![]() .
.
![]()
Problem 24
For each positive integer ![]() , let
, let ![]() denote the greatest prime factor of
denote the greatest prime factor of ![]() . For how many positive integers
. For how many positive integers ![]() is it true that both
is it true that both ![]() and
and ![]() ?
?
![]()
Problem 25
In ![]() we have
we have ![]() ,
, ![]() , and
, and ![]() . Points
. Points ![]() and
and ![]() are on
are on ![]() and
and ![]() respectively, with
respectively, with ![]() and
and ![]() . What is the ratio of the area of triangle
. What is the ratio of the area of triangle ![]() to the area of the quadrilateral
to the area of the quadrilateral ![]() ?
?
![]()