Difference between revisions of "2007 AIME II Problems"
(Replaced image with asymptote diagram) |
(→Problem 10) |
||
| (6 intermediate revisions by 5 users not shown) | |||
| Line 3: | Line 3: | ||
== Problem 1 == | == Problem 1 == | ||
A mathematical organization is producing a set of commemorative license plates. Each plate contains a sequence of five characters chosen from the four letters in AIME and the four digits in <math>2007</math>. No character may appear in a sequence more times than it appears among the four letters in AIME or the four digits in <math>2007</math>. A set of plates in which each possible sequence appears exactly once contains N license plates. Find N/10. | A mathematical organization is producing a set of commemorative license plates. Each plate contains a sequence of five characters chosen from the four letters in AIME and the four digits in <math>2007</math>. No character may appear in a sequence more times than it appears among the four letters in AIME or the four digits in <math>2007</math>. A set of plates in which each possible sequence appears exactly once contains N license plates. Find N/10. | ||
| + | |||
[[2007 AIME II Problems/Problem 1|Solution]] | [[2007 AIME II Problems/Problem 1|Solution]] | ||
| Line 55: | Line 56: | ||
== Problem 10 == | == Problem 10 == | ||
| − | Let <math>S</math> be a [[set]] with six [[element]]s. Let <math>P</math> be the set of all [[subset]]s of <math>S.</math> Subsets <math>A</math> and <math>B</math> of <math>S</math>, not necessarily distinct, are chosen independently and at random from <math>P</math>. The [[probability]] that <math>B</math> is contained in | + | Let <math>S</math> be a [[set]] with six [[element]]s. Let <math>\mathcal{P}</math> be the set of all [[subset]]s of <math>S.</math> Subsets <math>A</math> and <math>B</math> of <math>S</math>, not necessarily distinct, are chosen independently and at random from <math>\mathcal{P}</math>. The [[probability]] that <math>B</math> is contained in one of <math>A</math> or <math>S-A</math> is <math>\frac{m}{n^{r}},</math> where <math>m</math>, <math>n</math>, and <math>r</math> are [[positive]] [[integer]]s, <math>n</math> is [[prime]], and <math>m</math> and <math>n</math> are [[relatively prime]]. Find <math>m+n+r.</math> (The set <math>S-A</math> is the set of all elements of <math>S</math> which are not in <math>A.</math>) |
[[2007 AIME II Problems/Problem 10|Solution]] | [[2007 AIME II Problems/Problem 10|Solution]] | ||
| Line 96: | Line 97: | ||
[[2007 AIME II Problems/Problem 15|Solution]] | [[2007 AIME II Problems/Problem 15|Solution]] | ||
| + | |||
| + | {{AIME box|year=2007|n=II|before=[[2007 AIME I]]|after=[[2008 AIME I]]}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 01:45, 6 December 2021
| 2007 AIME II (Answer Key) | AoPS Contest Collections • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
Contents
Problem 1
A mathematical organization is producing a set of commemorative license plates. Each plate contains a sequence of five characters chosen from the four letters in AIME and the four digits in ![]() . No character may appear in a sequence more times than it appears among the four letters in AIME or the four digits in
. No character may appear in a sequence more times than it appears among the four letters in AIME or the four digits in ![]() . A set of plates in which each possible sequence appears exactly once contains N license plates. Find N/10.
. A set of plates in which each possible sequence appears exactly once contains N license plates. Find N/10.
Problem 2
Find the number of ordered triples ![]() where
where ![]() ,
, ![]() , and
, and ![]() are positive integers,
are positive integers, ![]() is a factor of
is a factor of ![]() ,
, ![]() is a factor of
is a factor of ![]() , and
, and ![]() .
.
Problem 3
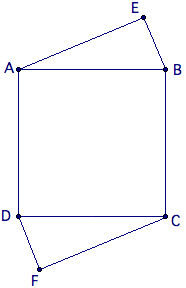
Square ![]() has side length
has side length ![]() , and points
, and points ![]() and
and ![]() are exterior to the square such that
are exterior to the square such that ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 4
The workers in a factory produce widgets and whoosits. For each product, production time is constant and identical for all workers, but not necessarily equal for the two products. In one hour, ![]() workers can produce
workers can produce ![]() widgets and
widgets and ![]() whoosits. In two hours,
whoosits. In two hours, ![]() workers can produce
workers can produce ![]() widgets and
widgets and ![]() whoosits. In three hours,
whoosits. In three hours, ![]() workers can produce
workers can produce ![]() widgets and
widgets and ![]() whoosits. Find
whoosits. Find ![]() .
.
Problem 5
The graph of the equation ![]() is drawn on graph paper with each square representing one unit in each direction. How many of the
is drawn on graph paper with each square representing one unit in each direction. How many of the ![]() by
by ![]() graph paper squares have interiors lying entirely below the graph and entirely in the first quadrant?
graph paper squares have interiors lying entirely below the graph and entirely in the first quadrant?
Problem 6
An integer is called parity-monotonic if its decimal representation ![]() satisfies
satisfies ![]() if
if ![]() is odd, and
is odd, and ![]() if
if ![]() is even. How many four-digit parity-monotonic integers are there?
is even. How many four-digit parity-monotonic integers are there?
Problem 7
Given a real number ![]() let
let ![]() denote the greatest integer less than or equal to
denote the greatest integer less than or equal to ![]() For a certain integer
For a certain integer ![]() there are exactly
there are exactly ![]() positive integers
positive integers ![]() such that
such that ![]() and
and ![]() divides
divides ![]() for all
for all ![]() such that
such that ![]()
Find the maximum value of ![]() for
for ![]()
Problem 8
A rectangular piece of paper measures 4 units by 5 units. Several lines are drawn parallel to the edges of the paper. A rectangle determined by the intersections of some of these lines is called basic if
- (i) all four sides of the rectangle are segments of drawn line segments, and
- (ii) no segments of drawn lines lie inside the rectangle.
Given that the total length of all lines drawn is exactly 2007 units, let ![]() be the maximum possible number of basic rectangles determined. Find the remainder when
be the maximum possible number of basic rectangles determined. Find the remainder when ![]() is divided by 1000.
is divided by 1000.
Problem 9
Rectangle ![]() is given with
is given with ![]() and
and ![]() Points
Points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() respectively, such that
respectively, such that ![]() The inscribed circle of triangle
The inscribed circle of triangle ![]() is tangent to
is tangent to ![]() at point
at point ![]() and the inscribed circle of triangle
and the inscribed circle of triangle ![]() is tangent to
is tangent to ![]() at point
at point ![]() Find
Find ![]()
Problem 10
Let ![]() be a set with six elements. Let
be a set with six elements. Let ![]() be the set of all subsets of
be the set of all subsets of ![]() Subsets
Subsets ![]() and
and ![]() of
of ![]() , not necessarily distinct, are chosen independently and at random from
, not necessarily distinct, are chosen independently and at random from ![]() . The probability that
. The probability that ![]() is contained in one of
is contained in one of ![]() or
or ![]() is
is ![]() where
where ![]() ,
, ![]() , and
, and ![]() are positive integers,
are positive integers, ![]() is prime, and
is prime, and ![]() and
and ![]() are relatively prime. Find
are relatively prime. Find ![]() (The set
(The set ![]() is the set of all elements of
is the set of all elements of ![]() which are not in
which are not in ![]() )
)
Problem 11
Two long cylindrical tubes of the same length but different diameters lie parallel to each other on a flat surface. The larger tube has radius ![]() and rolls along the surface toward the smaller tube, which has radius
and rolls along the surface toward the smaller tube, which has radius ![]() . It rolls over the smaller tube and continues rolling along the flat surface until it comes to rest on the same point of its circumference as it started, having made one complete revolution. If the smaller tube never moves, and the rolling occurs with no slipping, the larger tube ends up a distance
. It rolls over the smaller tube and continues rolling along the flat surface until it comes to rest on the same point of its circumference as it started, having made one complete revolution. If the smaller tube never moves, and the rolling occurs with no slipping, the larger tube ends up a distance ![]() from where it starts. The distance
from where it starts. The distance ![]() can be expressed in the form
can be expressed in the form ![]() where
where ![]()
![]() and
and ![]() are integers and
are integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
Problem 12
The increasing geometric sequence ![]() consists entirely of integral powers of
consists entirely of integral powers of ![]() Given that
Given that
 and
and 
find ![]()
Problem 13
A triangular array of squares has one square in the first row, two in the second, and in general, ![]() squares in the
squares in the ![]() th row for
th row for ![]() With the exception of the bottom row, each square rests on two squares in the row immediately below (illustrated in given diagram). In each square of the eleventh row, a
With the exception of the bottom row, each square rests on two squares in the row immediately below (illustrated in given diagram). In each square of the eleventh row, a ![]() or a
or a ![]() is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of
is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of ![]() 's and
's and ![]() 's in the bottom row is the number in the top square a multiple of
's in the bottom row is the number in the top square a multiple of ![]() ?
?
![[asy] for (int i=0; i<12; ++i){ for (int j=0; j<i; ++j){ //dot((-j+i/2,-i)); draw((-j+i/2,-i)--(-j+i/2+1,-i)--(-j+i/2+1,-i+1)--(-j+i/2,-i+1)--cycle); } } [/asy]](http://latex.artofproblemsolving.com/f/4/8/f482d8c340a42e4beffcdc4a965cff94810d48fc.png)
Problem 14
Let ![]() be a polynomial with real coefficients such that
be a polynomial with real coefficients such that ![]()
![]() and for all
and for all ![]() ,
, ![]() Find
Find ![]()
Problem 15
Four circles ![]()
![]()
![]() and
and ![]() with the same radius are drawn in the interior of triangle
with the same radius are drawn in the interior of triangle ![]() such that
such that ![]() is tangent to sides
is tangent to sides ![]() and
and ![]() ,
, ![]() to
to ![]() and
and ![]() ,
, ![]() to
to ![]() and
and ![]() , and
, and ![]() is externally tangent to
is externally tangent to ![]()
![]() and
and ![]() . If the sides of triangle
. If the sides of triangle ![]() are
are ![]()
![]() and
and ![]() the radius of
the radius of ![]() can be represented in the form
can be represented in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
| 2007 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by 2007 AIME I |
Followed by 2008 AIME I | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.