2007 AMC 12A Problems/Problem 20
Problem
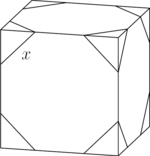
Corners are sliced off a unit cube so that the six faces each become regular octagons. What is the total volume of the removed tetrahedra?
![]()
Solution
Since the sides of a regular polygon are equal in length, we can call each side ![]() . Examine one edge of the unit cube: each contains two slanted diagonal edges of an octagon and one straight edge. The diagonal edges form
. Examine one edge of the unit cube: each contains two slanted diagonal edges of an octagon and one straight edge. The diagonal edges form ![]() right triangles, making the distance on the edge of the cube
right triangles, making the distance on the edge of the cube ![]() . Thus,
. Thus, ![]() , and
, and  .
.
Each of the cut off corners is a pyramid, whose volume can be calculated by ![]() . Use the base as one of the three congruent isosceles triangles, with the height being one of the edges of the pyramid that sits on the edges of the cube. The height is
. Use the base as one of the three congruent isosceles triangles, with the height being one of the edges of the pyramid that sits on the edges of the cube. The height is ![]() . The base is a
. The base is a ![]() with leg of length
with leg of length ![]() , making its area
, making its area ![]() . Plugging this in, we get that the area of one of the tetrahedra is
. Plugging this in, we get that the area of one of the tetrahedra is  . Since there are 8 removed corners, we get an answer of
. Since there are 8 removed corners, we get an answer of ![]()
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 19 |
Followed by Problem 21 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |