Difference between revisions of "2012 AIME I Problems/Problem 12"
m (→Solution 7) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 75: | Line 75: | ||
~ dolphin7 | ~ dolphin7 | ||
| + | |||
| + | |||
| + | ===Solution 7=== | ||
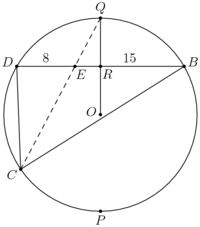
| + | WLOG, let <math>DE=8</math> and <math>BE=15</math>. First, by the Law of Sines on <math>\triangle CEB</math>, we find that | ||
| + | <cmath>\frac{\sin\angle B}{CE}=\frac{\sin\angle ECB}{BE}=\frac{1}{30}\implies \sin\angle B=\frac{CE}{30}.</cmath> | ||
| + | Now, we will find <math>CE</math>. Consider the following diagram: | ||
| + | [[Image:2012 AIME I -12 Sol 7 Diagram.png|200px|thumb|left| ]] | ||
| + | We have constructed equilateral triangle <math>\triangle BDP</math>, and its circumcircle. Since <math>\angle DCB=\angle DPB=60^\circ</math>, <math>C</math> lies on <math>(BDP)</math> as well. Let <math>Q</math> be the point diametrically opposite <math>P</math> on <math>(BCD)</math>, and let <math>R</math> be the foot of <math>Q</math> on <math>BD</math> (this is the midpoint of <math>BD</math>). It is easy to compute that <math>RQ=\frac{13}{\sqrt3}</math> and <math>ER=\frac{23}{2}-8=\frac{7}{2}</math>. Therefore, by the Pythagorean Theorem, <math>ER=\frac{169}{3}</math>. Now, by Power of a Point, we know that <math>(DE)(BE)=(EQ)(EC)</math>, which means that | ||
| + | <cmath>120=\frac{13EC}{\sqrt{3}}\implies EC=\frac{120\sqrt{3}}{13}.</cmath> | ||
| + | From before, we know that <math>\sin\angle B=\frac{EC}{30}\implies \sin\angle B=\frac{4\sqrt3}{13}</math>. It's now easy to compute <math>\cos\angle B</math> as well using the Pythagorean identity; we find that <math>\cos\angle B=\frac{11}{13}</math>, and thus <math>\tan\angle B=\frac{4\sqrt3}{11}</math> for an answer of <math>\boxed{018}</math>. | ||
| + | -brainiacmaniac31 | ||
== See also == | == See also == | ||
{{AIME box|year=2012|n=I|num-b=11|num-a=13}} | {{AIME box|year=2012|n=I|num-b=11|num-a=13}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 02:20, 3 June 2020
Contents
Problem 12
Let ![]() be a right triangle with right angle at
be a right triangle with right angle at ![]() Let
Let ![]() and
and ![]() be points on
be points on ![]() with
with ![]() between
between ![]() and
and ![]() such that
such that ![]() and
and ![]() trisect
trisect ![]() If
If ![]() then
then ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are relatively prime positive integers, and
are relatively prime positive integers, and ![]() is a positive integer not divisible by the square of any prime. Find
is a positive integer not divisible by the square of any prime. Find ![]()
Solutions
Solution 1
Let ![]() . Using angle bisector theorem on
. Using angle bisector theorem on ![]() ,
, ![]() , so
, so ![]() . Then, drop the altitude from
. Then, drop the altitude from ![]() to
to ![]() and call the foot
and call the foot ![]() . Thus,
. Thus, ![]() ,
, ![]() , and
, and ![]() . Finally,
. Finally, ![]() . Our answer is
. Our answer is ![]() .
.
Solution 2
Without loss of generality, set ![]() . Then, by the Angle Bisector Theorem on triangle
. Then, by the Angle Bisector Theorem on triangle ![]() , we have
, we have ![]() . We apply the Law of Cosines to triangle
. We apply the Law of Cosines to triangle ![]() to get
to get ![]() , which we can simplify to get
, which we can simplify to get ![]() .
.
Now, we have ![]() by another application of the Law of Cosines to triangle
by another application of the Law of Cosines to triangle ![]() , so
, so ![]() . In addition,
. In addition, ![]() , so
, so ![]() .
.
Our final answer is ![]() .
.
Solution 3
(This solution does not use the Angle Bisector Theorem or the Law of Cosines, but it uses the Law of Sines and more trig)
Find values for all angles in terms of ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Use the law of sines on ![]() and
and ![]() :
:
In ![]() ,
, ![]() . This simplifies to
. This simplifies to ![]() .
.
In ![]() ,
, ![]() . This simplifies to
. This simplifies to ![]() .
.
Solve for ![]() and equate them so that you get
and equate them so that you get ![]() .
.
From this, ![]() .
.
Use a trig identity on the denominator on the right to obtain: ![]()
This simplifies to ![]()
This gives ![]() Dividing by
Dividing by ![]() , we have
, we have ![]()
![]() . Our final answer is
. Our final answer is ![]() .
.
Solution 4
(This solution avoids advanced trigonometry)
Let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() , and let
, and let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() .
.
Now let ![]() . Clearly, triangles
. Clearly, triangles ![]() and
and ![]() are similar with
are similar with ![]() , so
, so ![]() .
.
Since triangles ![]() and
and ![]() are 30-60-90 right triangles, we can easily find other lengths in terms of
are 30-60-90 right triangles, we can easily find other lengths in terms of ![]() . For example, we see that
. For example, we see that ![]() and
and ![]() . Therefore
. Therefore ![]() .
.
Again using the fact that triangles ![]() and
and ![]() are similar, we see that
are similar, we see that ![]() , so
, so ![]() .
.
Thus  , and our answer is
, and our answer is ![]() .
.
Solution 5
(Another solution without trigonometry)
Extend ![]() to point
to point ![]() such that
such that ![]() . It is then clear that
. It is then clear that ![]() is similar to
is similar to ![]() .
.
Let ![]() ,
, ![]() . Then
. Then ![]() .
.
With the Angle Bisector Theorem, we get that ![]() . From 30-60-90
. From 30-60-90 ![]() , we get that
, we get that ![]() and
and ![]() .
.
From ![]() , we have that
, we have that ![]() . Simplifying yields
. Simplifying yields  , and
, and ![]() , so our answer is
, so our answer is ![]() .
.
Solution 6
Let ![]() , and let the feet of the altitudes from
, and let the feet of the altitudes from ![]() and
and ![]() to
to ![]() be
be ![]() and
and ![]() , respectively. Also, let
, respectively. Also, let ![]() and
and ![]() . We see that
. We see that ![]() and
and ![]() by right triangles
by right triangles ![]() and
and ![]() . From this we have that
. From this we have that ![]() . With the same triangles we have
. With the same triangles we have ![]() and
and ![]() . From 30-60-90 triangles
. From 30-60-90 triangles ![]() and
and ![]() , we see that
, we see that ![]() and
and ![]() , so
, so ![]() . From our two values of
. From our two values of ![]() we get:
we get:
![]()
![]()
 Our answer is then
Our answer is then ![]() .
.
Video Solution by Richard Rusczyk
https://artofproblemsolving.com/videos/amc/2012aimei/352
~ dolphin7
Solution 7
WLOG, let ![]() and
and ![]() . First, by the Law of Sines on
. First, by the Law of Sines on ![]() , we find that
, we find that
![]() Now, we will find
Now, we will find ![]() . Consider the following diagram:
. Consider the following diagram:
We have constructed equilateral triangle ![]() , and its circumcircle. Since
, and its circumcircle. Since ![]() ,
, ![]() lies on
lies on ![]() as well. Let
as well. Let ![]() be the point diametrically opposite
be the point diametrically opposite ![]() on
on ![]() , and let
, and let ![]() be the foot of
be the foot of ![]() on
on ![]() (this is the midpoint of
(this is the midpoint of ![]() ). It is easy to compute that
). It is easy to compute that ![]() and
and ![]() . Therefore, by the Pythagorean Theorem,
. Therefore, by the Pythagorean Theorem, ![]() . Now, by Power of a Point, we know that
. Now, by Power of a Point, we know that ![]() , which means that
, which means that
![]() From before, we know that
From before, we know that ![]() . It's now easy to compute
. It's now easy to compute ![]() as well using the Pythagorean identity; we find that
as well using the Pythagorean identity; we find that ![]() , and thus
, and thus ![]() for an answer of
for an answer of ![]() .
-brainiacmaniac31
.
-brainiacmaniac31
See also
| 2012 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.