Difference between revisions of "2017 AIME I Problems/Problem 4"
(→Solution) |
Mathboy282 (talk | contribs) (→Solution) |
||
| (26 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ==Problem | + | ==Problem == |
A pyramid has a triangular base with side lengths <math>20</math>, <math>20</math>, and <math>24</math>. The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length <math>25</math>. The volume of the pyramid is <math>m\sqrt{n}</math>, where <math>m</math> and <math>n</math> are positive integers, and <math>n</math> is not divisible by the square of any prime. Find <math>m+n</math>. | A pyramid has a triangular base with side lengths <math>20</math>, <math>20</math>, and <math>24</math>. The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length <math>25</math>. The volume of the pyramid is <math>m\sqrt{n}</math>, where <math>m</math> and <math>n</math> are positive integers, and <math>n</math> is not divisible by the square of any prime. Find <math>m+n</math>. | ||
==Solution== | ==Solution== | ||
| − | Let the triangular base be <math>\triangle ABC</math>, with <math>\overline {AB} = 24</math>. We find that the altitude to side <math>AB</math> is <math>16</math>, so the area of <math>\triangle ABC</math> is <math>(24*16)/2 = 192</math>. | + | Let the triangular base be <math>\triangle ABC</math>, with <math>\overline {AB} = 24</math>. We find that the altitude to side <math>\overline {AB}</math> is <math>16</math>, so the area of <math>\triangle ABC</math> is <math>(24*16)/2 = 192</math>. |
Let the fourth vertex of the tetrahedron be <math>P</math>, and let the midpoint of <math>\overline {AB}</math> be <math>M</math>. Since <math>P</math> is equidistant from <math>A</math>, <math>B</math>, and <math>C</math>, the line through <math>P</math> perpendicular to the plane of <math>\triangle ABC</math> will pass through the circumcenter of <math>\triangle ABC</math>, which we will call <math>O</math>. Note that <math>O</math> is equidistant from each of <math>A</math>, <math>B</math>, and <math>C</math>. Then, | Let the fourth vertex of the tetrahedron be <math>P</math>, and let the midpoint of <math>\overline {AB}</math> be <math>M</math>. Since <math>P</math> is equidistant from <math>A</math>, <math>B</math>, and <math>C</math>, the line through <math>P</math> perpendicular to the plane of <math>\triangle ABC</math> will pass through the circumcenter of <math>\triangle ABC</math>, which we will call <math>O</math>. Note that <math>O</math> is equidistant from each of <math>A</math>, <math>B</math>, and <math>C</math>. Then, | ||
| Line 9: | Line 9: | ||
<cmath>\overline {OM} + \overline {OC} = \overline {CM} = 16</cmath> | <cmath>\overline {OM} + \overline {OC} = \overline {CM} = 16</cmath> | ||
| − | Let <math>\overline {OM} = d</math>. | + | Let <math>\overline {OM} = d</math>. Then <math>OC=OA=\sqrt{d^2+12^2}.</math> |
Equation <math>(1)</math>: | Equation <math>(1)</math>: | ||
<cmath>d + \sqrt {d^2 + 144} = 16</cmath> | <cmath>d + \sqrt {d^2 + 144} = 16</cmath> | ||
| Line 31: | Line 31: | ||
Let the distance <math>\overline {OP} = h</math>. Using the Pythagorean Theorem on triangle <math>AOP</math>, <math>BOP</math>, or <math>COP</math> (all three are congruent by SSS): | Let the distance <math>\overline {OP} = h</math>. Using the Pythagorean Theorem on triangle <math>AOP</math>, <math>BOP</math>, or <math>COP</math> (all three are congruent by SSS): | ||
| − | <cmath>25^2 = h^2 + ( | + | <cmath>25^2 = h^2 + (25/2)^2</cmath> |
<cmath>625 = h^2 + 625/4</cmath> | <cmath>625 = h^2 + 625/4</cmath> | ||
| Line 47: | Line 47: | ||
This simplifies to <math>V = 800\sqrt {3}</math>, so <math>m+n = \boxed {803}</math>. | This simplifies to <math>V = 800\sqrt {3}</math>, so <math>m+n = \boxed {803}</math>. | ||
| − | Solution | + | |
| + | NOTE : If you don’t know or remember the formula for the volume of a triangular pyramid, you can derive it using calculus as follows : | ||
| + | |||
| + | Take a small triangular element in the pyramid. We know that it’s area is proportional to the height from the vertex to the base. Hence, we know that <math>\frac{A_{small element}}{A} = \frac{h^2}{H^2} \implies A_{small element} = \frac{Ah^2}{H^2}</math>. Now integrate it taking the limits <math>0</math> to <math>H</math> | ||
| + | |||
| + | ===Shortcut=== | ||
| + | Here is a shortcut for finding the radius <math>R</math> of the circumcenter of <math>\triangle ABC</math>. | ||
| + | |||
| + | As before, we find that the foot of the altitude from <math>P</math> lands on the circumcenter of <math>\triangle ABC</math>. Let <math>BC=a</math>, <math>AC=b</math>, and <math>AB=c</math>. | ||
| + | Then we write the area of <math>\triangle ABC</math> in two ways: | ||
| + | <cmath>[ABC]= \frac{1}{2} \cdot 24 \cdot 16 = \frac{abc}{4R}</cmath> | ||
| + | |||
| + | Plugging in <math>20</math>, <math>20</math>, and <math>24</math> for <math>a</math>, <math>b</math>, and <math>c</math> respectively, and solving for <math>R</math>, we obtain <math>R= \frac{25}{2}=OA=OB=OC</math>. | ||
| + | |||
| + | Then continue as before to use the Pythagorean Theorem on <math>\triangle AOP</math>, find <math>h</math>, and find the volume of the pyramid. | ||
| + | |||
| + | ===Another Shortcut (Extended Law of Sines)=== | ||
| + | Take the base <math>\triangle ABC</math>, where <math>AB = BC = 20</math> and <math>AC = 24</math>. Draw an altitude from <math>B</math> to <math>AC</math> that bisects <math>AC</math> at point <math>D</math>. Then the altitude has length <math>\sqrt{20^2 - 12^2} = \sqrt{16^2} = 16</math>. Next, let <math>\angle BCA = \theta</math>. Then from the right triangle <math>\triangle BDC</math>, <math>\sin \theta = 4/5</math>. From the extended law of sines, the circumradius is <math>20 \cdot \dfrac{5}{4} \cdot \dfrac{1}{2} = \dfrac{25}{2}</math>. | ||
| + | |||
| + | ==Solution 2 (Coordinates)== | ||
| + | |||
| + | We can place a three dimensional coordinate system on this pyramid. WLOG assume the vertex across from the line that has length <math>24</math> is at the origin, or <math>(0, 0, 0)</math>. Then, the two other vertices can be <math>(-12, -16, 0)</math> and <math>(12, -16, 0)</math>. Let the fourth vertex have coordinates of <math>(x, y, z)</math>. We have the following <math>3</math> equations from the distance formula. | ||
| + | |||
| + | <cmath>x^2+y^2+z^2=625</cmath> | ||
| + | |||
| + | <cmath>(x+12)^2+(y+16)^2+z^2=625</cmath> | ||
| + | |||
| + | <cmath>(x-12)^2+(y+16)^2+z^2=625</cmath> | ||
| + | |||
| + | Adding the last two equations and substituting in the first equation, we get that <math>y=-\frac{25}{2}</math>. If you drew a good diagram, it should be obvious that <math>x=0</math>. Now, solving for <math>z</math>, we get that <math>z=\frac{25\sqrt{3}}{2}</math>. So, the height of the pyramid is <math>\frac{25\sqrt{3}}{2}</math>. The base is equal to the area of the triangle, which is <math>\frac{1}{2} \cdot 24 \cdot 16 = 192</math>. The volume is <math>\frac{1}{3} \cdot 192 \cdot \frac{25\sqrt{3}}{2} = 800\sqrt{3}</math>. Thus, the answer is <math>800+3 = \boxed{803}</math>. | ||
| + | |||
| + | '''-RootThreeOverTwo''' | ||
| + | |||
| + | ==Solution 3 (Heron's Formula)== | ||
| + | |||
| + | Label the four vertices of the tetrahedron and the midpoint of <math>\overline {AB}</math>, and notice that the area of the base of the tetrahedron, <math>\triangle ABC</math>, equals <math>192</math>, according to Solution 1. | ||
| + | |||
| + | Notice that the altitude of <math>\triangle CPM</math> from <math>\overline {CM}</math> to point <math>P</math> is the height of the tetrahedron. Side <math>\overline {PM}</math> is can be found using the Pythagorean Theorem on <math>\triangle APM</math>, giving us <math>\overline {PM}=\sqrt{481}.</math> | ||
| + | |||
| + | Using Heron's Formula, the area of <math>\triangle CPM</math> can be written as | ||
| + | <cmath>\sqrt{\frac{41+\sqrt{481}}{2}(\frac{41+\sqrt{481}}{2}-16)(\frac{41+\sqrt{481}}{2}-25)(\frac{41+\sqrt{481}}{2}-\sqrt{481})}</cmath> | ||
| + | <cmath>=\frac{\sqrt{(41+\sqrt{481})(9+\sqrt{481})(-9+\sqrt{481})(41-\sqrt{481})}}{4}</cmath> | ||
| + | |||
| + | Notice that both <math>(41+\sqrt{481})(41-\sqrt{481})</math> and <math>(9+\sqrt{481})(-9+\sqrt{481})</math> can be rewritten as differences of squares; thus, the expression can be written as | ||
| + | <cmath>\frac{\sqrt{(41^2-481)(481-9^2)}}{4}=\frac{\sqrt{480000}}{4}=100\sqrt{3}.</cmath> | ||
| + | |||
| + | From this, we can determine the height of both <math>\triangle CPM</math> and tetrahedron <math>ABCP</math> to be <math>\frac{100\sqrt{3}}{8}</math>; therefore, the volume of the tetrahedron equals <math>\frac{100\sqrt{3}}{8} \cdot 192=800\sqrt{3}</math>; thus, <math>m+n=800+3=\boxed{803}.</math> | ||
| + | |||
| + | '''-dzhou100''' | ||
| + | |||
| + | |||
| + | ==Solution 4 (Symmetry)== | ||
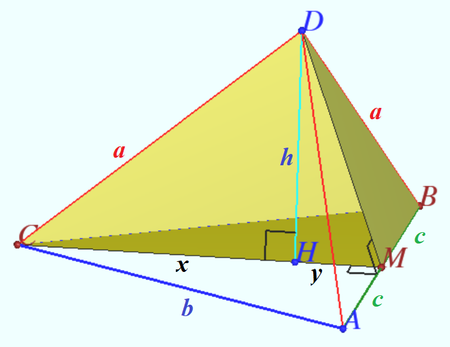
| + | [[File:2017 AIME I 4.png|450px|right]] | ||
| + | |||
| + | Notation is shown on diagram. | ||
| + | <cmath>AM = MB = c = 12, AC = BC = b = 20,</cmath> | ||
| + | <cmath>DA = DB = DC = a = 25.</cmath> | ||
| + | <cmath>CM = x + y = \sqrt{b^2-c^2} = 16,</cmath> | ||
| + | <cmath>x^2 - y^2 = CD^2 – DM^2 = CD^2 – (BD^2 – BM^2) = c^2 = 144,</cmath> | ||
| + | <cmath>x – y = \frac{x^2 – y^2}{x+y} = \frac {c^2} {16} = 9,</cmath> | ||
| + | <cmath>x = \frac {16 + 9}{2} = \frac {a}{2},</cmath> | ||
| + | <cmath>h = \sqrt{a^2 -\frac{ a^2}{4}} = a \frac {\sqrt{3}}{2},</cmath> | ||
| + | <cmath>V = \frac{h\cdot CM \cdot c}{3}= \frac{16\cdot 25 \sqrt{3} \cdot 12}{3} = 800 \sqrt{3} \implies \boxed {803}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/Mk-MCeVjSGc | ||
| + | ~Shreyas S | ||
==See Also== | ==See Also== | ||
{{AIME box|year=2017|n=I|num-b=3|num-a=5}} | {{AIME box|year=2017|n=I|num-b=3|num-a=5}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 15:55, 5 January 2024
Contents
Problem
A pyramid has a triangular base with side lengths ![]() ,
, ![]() , and
, and ![]() . The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length
. The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length ![]() . The volume of the pyramid is
. The volume of the pyramid is ![]() , where
, where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Solution
Let the triangular base be ![]() , with
, with ![]() . We find that the altitude to side
. We find that the altitude to side ![]() is
is ![]() , so the area of
, so the area of ![]() is
is ![]() .
.
Let the fourth vertex of the tetrahedron be ![]() , and let the midpoint of
, and let the midpoint of ![]() be
be ![]() . Since
. Since ![]() is equidistant from
is equidistant from ![]() ,
, ![]() , and
, and ![]() , the line through
, the line through ![]() perpendicular to the plane of
perpendicular to the plane of ![]() will pass through the circumcenter of
will pass through the circumcenter of ![]() , which we will call
, which we will call ![]() . Note that
. Note that ![]() is equidistant from each of
is equidistant from each of ![]() ,
, ![]() , and
, and ![]() . Then,
. Then,
![]()
Let ![]() . Then
. Then ![]() Equation
Equation ![]() :
:
![]()
Squaring both sides, we have
![]()
![]()
![]()
Substituting with equation ![]() :
:
![]()
![]()
We now find that ![]() .
.
Let the distance ![]() . Using the Pythagorean Theorem on triangle
. Using the Pythagorean Theorem on triangle ![]() ,
, ![]() , or
, or ![]() (all three are congruent by SSS):
(all three are congruent by SSS):
![]()
![]()
![]()
![]()
Finally, by the formula for volume of a pyramid,
![]()
![]() This simplifies to
This simplifies to ![]() , so
, so ![]() .
.
NOTE : If you don’t know or remember the formula for the volume of a triangular pyramid, you can derive it using calculus as follows :
Take a small triangular element in the pyramid. We know that it’s area is proportional to the height from the vertex to the base. Hence, we know that ![]() . Now integrate it taking the limits
. Now integrate it taking the limits ![]() to
to ![]()
Shortcut
Here is a shortcut for finding the radius ![]() of the circumcenter of
of the circumcenter of ![]() .
.
As before, we find that the foot of the altitude from ![]() lands on the circumcenter of
lands on the circumcenter of ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() .
Then we write the area of
.
Then we write the area of ![]() in two ways:
in two ways:
![]()
Plugging in ![]() ,
, ![]() , and
, and ![]() for
for ![]() ,
, ![]() , and
, and ![]() respectively, and solving for
respectively, and solving for ![]() , we obtain
, we obtain ![]() .
.
Then continue as before to use the Pythagorean Theorem on ![]() , find
, find ![]() , and find the volume of the pyramid.
, and find the volume of the pyramid.
Another Shortcut (Extended Law of Sines)
Take the base ![]() , where
, where ![]() and
and ![]() . Draw an altitude from
. Draw an altitude from ![]() to
to ![]() that bisects
that bisects ![]() at point
at point ![]() . Then the altitude has length
. Then the altitude has length ![]() . Next, let
. Next, let ![]() . Then from the right triangle
. Then from the right triangle ![]() ,
, ![]() . From the extended law of sines, the circumradius is
. From the extended law of sines, the circumradius is ![]() .
.
Solution 2 (Coordinates)
We can place a three dimensional coordinate system on this pyramid. WLOG assume the vertex across from the line that has length ![]() is at the origin, or
is at the origin, or ![]() . Then, the two other vertices can be
. Then, the two other vertices can be ![]() and
and ![]() . Let the fourth vertex have coordinates of
. Let the fourth vertex have coordinates of ![]() . We have the following
. We have the following ![]() equations from the distance formula.
equations from the distance formula.
![]()
![]()
![]()
Adding the last two equations and substituting in the first equation, we get that ![]() . If you drew a good diagram, it should be obvious that
. If you drew a good diagram, it should be obvious that ![]() . Now, solving for
. Now, solving for ![]() , we get that
, we get that ![]() . So, the height of the pyramid is
. So, the height of the pyramid is ![]() . The base is equal to the area of the triangle, which is
. The base is equal to the area of the triangle, which is ![]() . The volume is
. The volume is ![]() . Thus, the answer is
. Thus, the answer is ![]() .
.
-RootThreeOverTwo
Solution 3 (Heron's Formula)
Label the four vertices of the tetrahedron and the midpoint of ![]() , and notice that the area of the base of the tetrahedron,
, and notice that the area of the base of the tetrahedron, ![]() , equals
, equals ![]() , according to Solution 1.
, according to Solution 1.
Notice that the altitude of ![]() from
from ![]() to point
to point ![]() is the height of the tetrahedron. Side
is the height of the tetrahedron. Side ![]() is can be found using the Pythagorean Theorem on
is can be found using the Pythagorean Theorem on ![]() , giving us
, giving us ![]()
Using Heron's Formula, the area of ![]() can be written as
can be written as
![\[\sqrt{\frac{41+\sqrt{481}}{2}(\frac{41+\sqrt{481}}{2}-16)(\frac{41+\sqrt{481}}{2}-25)(\frac{41+\sqrt{481}}{2}-\sqrt{481})}\]](http://latex.artofproblemsolving.com/2/7/8/278f3e6d616ab6099179415faa1131424b27345b.png)
![\[=\frac{\sqrt{(41+\sqrt{481})(9+\sqrt{481})(-9+\sqrt{481})(41-\sqrt{481})}}{4}\]](http://latex.artofproblemsolving.com/c/9/7/c975061310c6fd5461db407f319886c7e19c968a.png)
Notice that both ![]() and
and ![]() can be rewritten as differences of squares; thus, the expression can be written as
can be rewritten as differences of squares; thus, the expression can be written as
![]()
From this, we can determine the height of both ![]() and tetrahedron
and tetrahedron ![]() to be
to be ![]() ; therefore, the volume of the tetrahedron equals
; therefore, the volume of the tetrahedron equals ![]() ; thus,
; thus, ![]()
-dzhou100
Solution 4 (Symmetry)
Notation is shown on diagram.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
https://youtu.be/Mk-MCeVjSGc ~Shreyas S
See Also
| 2017 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.