Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2019 AIME II Problems/Problem 7"

(→‎Solution 3)
(I decided to undo: The changes in the diagram section SHOULD NOT label more than the problem statement says. We should leave for the readers to assign points.)
(One intermediate revision by one other user not shown)
(No difference)

Revision as of 22:25, 4 November 2022

Problem

Triangle $ABC$ has side lengths $AB=120,BC=220$, and $AC=180$. Lines $\ell_A,\ell_B$, and $\ell_C$ are drawn parallel to $\overline{BC},\overline{AC}$, and $\overline{AB}$, respectively, such that the intersections of $\ell_A,\ell_B$, and $\ell_C$ with the interior of $\triangle ABC$ are segments of lengths $55,45$, and $15$, respectively. Find the perimeter of the triangle whose sides lie on lines $\ell_A,\ell_B$, and $\ell_C$.

Diagram

[asy] /* Made by MRENTHUSIASM */ size(350); pair A, B, C, D, E, F, G, H, I, J, K, L; B = origin; C = (220,0); A = intersectionpoints(Circle(B,120),Circle(C,180))[0]; D = A+1/4*(B-A); E = A+1/4*(C-A); F = B+1/4*(A-B); G = B+1/4*(C-B); H = C+1/8*(A-C); I = C+1/8*(B-C); J = extension(D,E,F,G); K = extension(F,G,H,I); L = extension(H,I,D,E); draw(A--B--C--cycle); draw(J+9/8*(K-J)--K+9/8*(J-K),dashed); draw(L+9/8*(K-L)--K+9/8*(L-K),dashed); draw(J+9/8*(L-J)--L+9/8*(J-L),dashed); draw(D--E^^F--G^^H--I,red); dot("$B$",B,1.5SW,linewidth(4)); dot("$C$",C,1.5SE,linewidth(4)); dot("$A$",A,1.5N,linewidth(4)); dot(D,linewidth(4)); dot(E,linewidth(4)); dot(F,linewidth(4)); dot(G,linewidth(4)); dot(H,linewidth(4)); dot(I,linewidth(4)); dot(J,linewidth(4)); dot(K,linewidth(4)); dot(L,linewidth(4)); label("$55$",midpoint(D--E),S,red); label("$45$",midpoint(F--G),dir(55),red); label("$15$",midpoint(H--I),dir(160),red); label("$\ell_A$",J+9/8*(L-J),1.5*dir(B--C)); label("$\ell_B$",K+9/8*(J-K),1.5*dir(C--A)); label("$\ell_C$",L+9/8*(K-L),1.5*dir(A--B)); [/asy] ~MRENTHUSIASM

Solution 1

Let the points of intersection of $\ell_A, \ell_B,\ell_C$ with $\triangle ABC$ divide the sides into consecutive segments $BD,DE,EC,CF,FG,GA,AH,HI,IB$. Furthermore, let the desired triangle be $\triangle XYZ$, with $X$ closest to side $BC$, $Y$ closest to side $AC$, and $Z$ closest to side $AB$. Hence, the desired perimeter is $XE+EF+FY+YG+GH+HZ+ZI+ID+DX=(DX+XE)+(FY+YG)+(HZ+ZI)+115$ since $HG=55$, $EF=15$, and $ID=45$.

Note that $\triangle AHG\sim \triangle BID\sim \triangle EFC\sim \triangle ABC$, so using similar triangle ratios, we find that $BI=HA=30$, $BD=HG=55$, $FC=\frac{45}{2}$, and $EC=\frac{55}{2}$.

We also notice that $\triangle EFC\sim \triangle YFG\sim \triangle EXD$ and $\triangle BID\sim \triangle HIZ$. Using similar triangles, we get that \[FY+YG=\frac{GF}{FC}\cdot \left(EF+EC\right)=\frac{225}{45}\cdot \left(15+\frac{55}{2}\right)=\frac{425}{2}\] \[DX+XE=\frac{DE}{EC}\cdot \left(EF+FC\right)=\frac{275}{55}\cdot \left(15+\frac{45}{2}\right)=\frac{375}{2}\] \[HZ+ZI=\frac{IH}{BI}\cdot \left(ID+BD\right)=2\cdot \left(45+55\right)=200\] Hence, the desired perimeter is $200+\frac{425+375}{2}+115=600+115=\boxed{715}$ -ktong

Solution 2

Let the diagram be set up like that in Solution 1.

By similar triangles we have \[\frac{AH}{AB}=\frac{GH}{BC}\Longrightarrow AH=30\] \[\frac{IB}{AB}=\frac{DI}{AC}\Longrightarrow IB=30\] Thus \[HI=AB-AH-IB=60\]

Since $\bigtriangleup IHZ\sim\bigtriangleup ABC$ and $\frac{HI}{AB}=\frac{1}{2}$, the altitude of $\bigtriangleup IHZ$ from $Z$ is half the altitude of $\bigtriangleup ABC$ from $C$, say $\frac{h}{2}$. Also since $\frac{EF}{AB}=\frac{1}{8}$, the distance from $\ell_C$ to $AB$ is $\frac{7}{8}h$. Therefore the altitude of $\bigtriangleup XYZ$ from $Z$ is \[\frac{1}{2}h+\frac{7}{8}h=\frac{11}{8}h\].

By triangle scaling, the perimeter of $\bigtriangleup XYZ$ is $\frac{11}{8}$ of that of $\bigtriangleup ABC$, or \[\frac{11}{8}(220+180+120)=\boxed{715}\]

~ Nafer

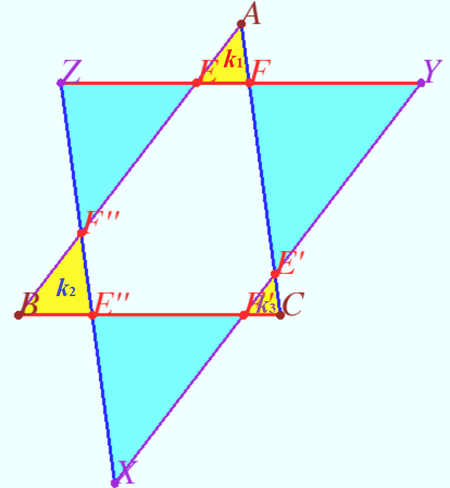
Solution 3

2019 AIME II 7.png

Notation shown on diagram. By similar triangles we have \[k_1 = \frac{EF}{BC} = \frac{AE}{AB} = \frac {AF}{AC} = \frac {1}{4},\] \[k_2 = \frac{F''E''}{AC} = \frac {BF''}{AB} = \frac{1}{4},\] \[k_3 = \frac{E'F'}{AB} = \frac{E'C }{AC} = \frac{1}{8}.\] So, \[\frac{ZE}{BC} = \frac{F''E}{AB} = \frac{AB - AE - BF''}{AB} = 1 - k_1 - k_2,\] \[\frac{FY}{BC} = \frac{FE'}{AC} = \frac{AC - AF - CE'}{AC} = 1 - k_1 - k_3.\] \[k = \frac{ZY}{BC} = \frac{ZE + EF + FY}{BC} = (1 - k_1 - k_2) + k_1 + (1 - k_1 - k_3)\] \[k = 2 - k_1 - k_2 - k_3 = 2 - \frac{1}{4} - \frac{1}{4} - \frac{1}{8} = \frac{11}{8}.\] \[\frac{ZY+YX +XZ}{BC +AB + AC} = k \implies ZY + YX + XZ =\frac{11}{8} (220 + 120 + 180) = \boxed {715}.\] vladimir.shelomovskii@gmail.com, vvsss

See Also

2019 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 6 		Followed by
Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2019_AIME_II_Problems/Problem_7&oldid=180177"