Difference between revisions of "2021 Fall AMC 12B Problems/Problem 24"
Kevinmathz (talk | contribs) (→Solution) |
Isabelchen (talk | contribs) m (→Solution 1 (Reflection)) |
||
| (27 intermediate revisions by 12 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ==Solution== | + | ==Problem== |
| + | |||
| + | Triangle <math>ABC</math> has side lengths <math>AB = 11, BC=24</math>, and <math>CA = 20</math>. The bisector of <math>\angle{BAC}</math> intersects <math>\overline{BC}</math> in point <math>D</math>, and intersects the circumcircle of <math>\triangle{ABC}</math> in point <math>E \ne A</math>. The circumcircle of <math>\triangle{BED}</math> intersects the line <math>AB</math> in points <math>B</math> and <math>F \ne B</math>. What is <math>CF</math>? | ||
| + | |||
| + | <math>\textbf{(A) } 28 \qquad \textbf{(B) } 20\sqrt{2} \qquad \textbf{(C) } 30 \qquad \textbf{(D) } 32 \qquad \textbf{(E) } 20\sqrt{3}</math> | ||
| + | |||
| + | ==Solution 1 (Reflection)== | ||
| + | |||
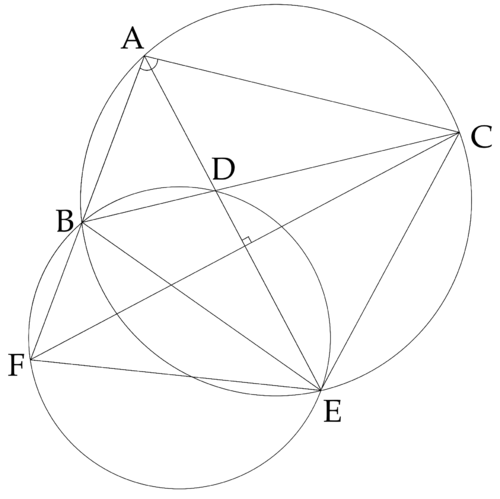
| + | [[File:2021AMC12BFallP24.png|center|500px]] | ||
| + | |||
| + | By the Law of Cosine <math>\cos A = \frac{AC^2 + AB^2 - BC^2}{ 2 \cdot AC \cdot AB} = \frac{20^2 + 11^2 - 24^2}{2\cdot20\cdot11} = -\frac18</math> | ||
| + | |||
| + | As <math>ABEC</math> is a cyclic quadrilateral, <math>\angle CEA = \angle CBA</math>. As <math>BDEF</math> is a cyclic quadrilateral, <math>\angle CBA = \angle FEA</math>. | ||
| + | |||
| + | <math>\because \quad \angle CEA = \angle FEA \quad \text{and} \quad \angle CAE = \angle FAE</math> | ||
| + | |||
| + | <math>\therefore \quad \triangle AFE \cong \triangle ACE</math> by <math>ASA</math> | ||
| + | |||
| + | Hence, <math>AF = AC = 20</math> | ||
| + | |||
| + | By the Law of Cosine <math>CF = \sqrt{20^2 + 20^2 - 2 \cdot 20 \cdot 20 (-\frac18)} = \sqrt{900} = \boxed{\textbf{C}~\text{30}}</math> | ||
| + | |||
| + | Note that <math>F</math> is <math>C</math>'s reflection over line <math>AE</math>, quadrilateral <math>ACEF</math> is a kite symmetrical by line <math>AE</math>, <math>AE \perp CF</math>. | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen] | ||
| + | |||
| + | ==Solution 2 (Olympiad Solution using Spiral Similarity)== | ||
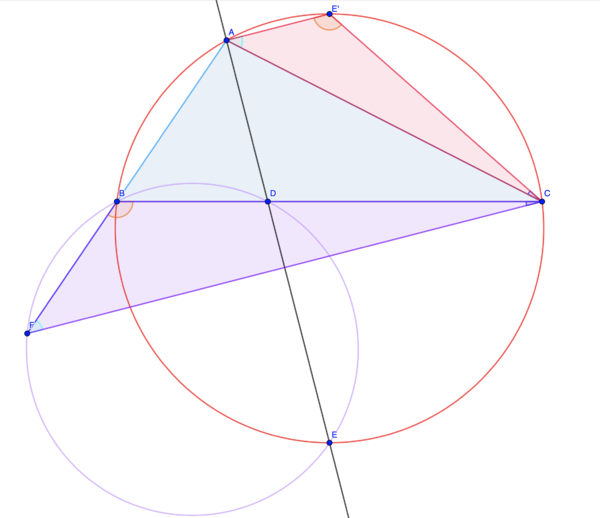
| + | Construct the <math>E</math>-antipode, <math>E^{\prime}\in(ABC)</math>. Notice <math>\triangle CE^{\prime}A\stackrel{+}{\sim}\triangle CBF</math> by spiral similarity at <math>C</math>, thus <math>CF=\dfrac{CB\cdot CA}{CE^{\prime}}=\frac{480}{CE^{\prime}}</math>. Let <math>CE^{\prime}=x</math>; by symmetry <math>BE^{\prime}=x</math> as well and <math>\cos\angle BE^{\prime}C=\cos\angle A=\tfrac{11^{2}+20^{2}-24^{2}}{2\cdot 11\cdot 20}=-\tfrac{1}{8}</math> from Law of Cosines in <math>\triangle ABC</math>, so by Law of Cosines in <math>\triangle BE^{\prime}C</math> we have <cmath>x^{2}+x^{2}+\left(2x^{2}\right)\left(-\dfrac{1}{8}\right)=24^{2}</cmath> from which <math>x=16</math>. Now, <math>CF=\dfrac{480}{16}=\boxed{\textbf{C}~\text{30}}</math>. | ||
| + | |||
| + | [[File:AMC 12 2021B Fall-24 Geogebra Diagram.png|600px]] | ||
| + | |||
| + | ==Solution 3== | ||
<b>Claim:</b> <math>\triangle ADC \sim \triangle ABE.</math> | <b>Claim:</b> <math>\triangle ADC \sim \triangle ABE.</math> | ||
| Line 5: | Line 36: | ||
<b>Proof:</b> Note that <math>\angle CAD = \angle CAE = \angle EAB</math> and <math>\angle DCA = \angle BCA = \angle BEA</math> meaning that our claim is true by AA similarity. | <b>Proof:</b> Note that <math>\angle CAD = \angle CAE = \angle EAB</math> and <math>\angle DCA = \angle BCA = \angle BEA</math> meaning that our claim is true by AA similarity. | ||
| − | Because of this similarity, we have that <cmath>\frac{AC}{AD} = \frac{AE}{AB} \ | + | Because of this similarity, we have that <cmath>\frac{AC}{AD} = \frac{AE}{AB} \Longrightarrow AB \cdot AC = AD \cdot AE = AB \cdot AF</cmath> by Power of a Point. Thus, <math>AC=AF=20.</math> |
| + | |||
| + | Two solution methods follow from here. | ||
| + | |||
| + | ===Solution 3.1 (Stewart's theorem)=== | ||
| + | |||
| + | Applying [[Stewart's theorem]] on <math>\triangle ABC</math> with cevian <math>\overline{CF}</math> using the [[Directed legnths|directed lengths]] <math>AF = AC = 20</math> and <math>FB = 11-20 = -9</math>, we obtain <cmath>\begin{align*} (20)(-9)(11) + (CF)(11)(CF) &= (24)(20)(24) + (20)(-9)(20) \\ 11CF^{2} - 1980 &= 11520 - 3600\end{align*}</cmath> so <math>CF=\sqrt{\frac{11520 - 3600 + 1980}{11}}=\sqrt{\frac{9900}{11}}=\sqrt{900}=\boxed{\textbf{(C) }30}</math>. | ||
| + | |||
| + | ===Solution 3.2 (Double Cosine Law)=== | ||
| + | |||
| + | Note that <math>\angle CAF = \angle CAB</math> so we may plug into Law of Cosines to find the angle's cosine: <cmath>AB^2+AC^2-2\cdot AB \cdot AC \cdot \cos(\angle CAB) = BC^2 \to \cos(\angle CAB) = -\frac{1}{8}.</cmath> | ||
| + | |||
| + | So, we observe that we can use Law of Cosines again to find <math>CF</math>: <cmath>CF^2 = AF^2+AC^2-2 \cdot AF \cdot AC \cdot \cos(\angle CAF) = 900 \to CF=\boxed{\textbf{(C) }30}</cmath> both ways. | ||
| + | |||
| + | - Kevinmathz | ||
| + | |||
| + | == Solution 4 == | ||
| + | This solution is based on this figure: [[file:2021_AMC_12B_(Nov)_Problem_24,_sol.png]] | ||
| + | |||
| + | Denote by <math>O</math> the circumcenter of <math>\triangle BED</math>. | ||
| + | Denote by <math>R</math> the circumradius of <math>\triangle BED</math>. | ||
| + | |||
| + | In <math>\triangle BCF</math>, following from the law of cosines, we have | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | CF^2 & = BC^2 + BF^2 - 2 BC \cdot BF \cos \angle CBF \\ | ||
| + | & = BC^2 + BF^2 + 2 BC \cdot BF \cos \angle ABC . \hspace{1cm} (1) | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | For <math>BF</math>, we have | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | BF & = 2 R \cos \angle FBO \\ | ||
| + | & = 2 R \cos \left( 180^\circ - \angle ABC - \angle CBO \right) \\ | ||
| + | & = 2 R \cos \left( 180^\circ - \angle ABC - \frac{180^\circ - \angle BOD}{2} \right) \\ | ||
| + | & = 2 R \cos \left( 180^\circ - \angle ABC - \frac{180^\circ - 2 \angle BED}{2} \right) \\ | ||
| + | & = 2 R \cos \left( 180^\circ - \angle ABC - \frac{180^\circ - 2 \angle BCA}{2} \right) \\ | ||
| + | & = 2 R \cos \left( 90^\circ - \angle ABC + \angle BCA \right) \\ | ||
| + | & = 2 R \sin \left( \angle ABC - \angle BCA \right) \\ | ||
| + | & = \frac{BD}{\sin \angle BED} \sin \left( \angle ABC - \angle BCA \right) \\ | ||
| + | & = \frac{BD}{\sin \angle BCA} \sin \left( \angle ABC - \angle BCA \right) \\ | ||
| + | & = BD \left( \sin \angle ABC \cot \angle BCA - \cos \angle ABC \right) . \hspace{1cm} (2) | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | The fourth equality follows from the property that <math>B</math>, <math>D</math>, <math>E</math> are concyclic. | ||
| + | The fifth and the ninth equalities follow from the property that <math>A</math>, <math>B</math>, <math>C</math>, <math>E</math> are concyclic. | ||
| + | |||
| + | Because <math>AD</math> bisects <math>\angle BAC</math>, following from the angle bisector theorem, we have | ||
| + | <cmath> | ||
| + | \[ | ||
| + | \frac{BD}{CD} = \frac{AB}{AC} . | ||
| + | \] | ||
| + | </cmath> | ||
| + | Hence, <math>BD = \frac{24 \cdot 11}{31}</math>. | ||
| + | |||
| + | In <math>\triangle ABC</math>, following from the law of cosines, we have | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | \cos \angle ABC & = \frac{AB^2 + BC^2 - AC^2}{2 AB \cdot BC} \\ | ||
| + | & = \frac{9}{16} | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | and | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | \cos \angle BCA & = \frac{AC^2 + BC^2 - AB^2}{2 AC \cdot BC} \\ | ||
| + | & = \frac{57}{64} . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | Hence, <math>\sin \angle ABC = \frac{5 \sqrt{7}}{16}</math> and <math>\sin \angle BCA = \frac{11 \sqrt{7}}{64}</math>. | ||
| + | Hence, <math>\cot \angle BCA = \frac{57}{11 \sqrt{7}}</math>. | ||
| + | |||
| + | Now, we are ready to compute <math>BF</math> whose expression is given in Equation (2). | ||
| + | We get <math>BF = 9</math>. | ||
| + | |||
| + | Now, we can compute <math>CF</math> whose expression is given in Equation (1). | ||
| + | We have <math>CF = 30</math>. | ||
| + | |||
| + | Therefore, the answer is <math>\boxed{\textbf{(C) }30}</math>. | ||
| + | |||
| + | ~Steven Chen (www.professorchenedu.com) | ||
| + | |||
| + | ==Solution 5== | ||
| + | Denote <math>B=(0, 0)</math> and <math>C=(24, 0)</math>. Note that by Heron's formula the area of <math>\triangle ABC</math> is <math>\frac{165\sqrt{7}}{4}</math> so the <math>y</math>-coordinate of <math>A</math> (height of <math>A</math> above the <math>x</math>-axis) is easily computed by the base-height formula as <math>\frac{55\sqrt7}{16}</math>. | ||
| + | |||
| + | Now, since <math>AB=11</math>, the <math>x</math>-coordinate of <math>A</math> satisfies <math>x^2+(\frac{55\sqrt7}{16})^2=11^2</math> and solving gives <math>x=\frac{99}{16}</math>. | ||
| + | |||
| + | The circumcircle of <math>\triangle ABC</math> has radius <math>\frac{abc}{4A}=\frac{11\cdot 24\cdot 20}{165\sqrt7}=\frac{32}{\sqrt7}</math>. We know by the perpendicular bisector rule that the circumcenter <math>O</math> is located directly below the midpoint of <math>\overline{BC}</math> (<math>x</math>-coordinate <math>12</math>). | ||
| + | |||
| + | So, the negative <math>y</math> coordinate of <math>O</math> satisfies <math>12^2+y^2=(\frac{32}{\sqrt7})^2</math> and solving gives <math>y=-\frac{4}{\sqrt7}</math>. | ||
| + | |||
| + | It's also clear that point <math>E</math> is going to be located directly below <math>O</math> on the circle, because the angle bisector intersects the circumcircle at the midpoint of the arc (Fact 5). Since the radius of the circle is <math>\frac{32}{\sqrt7}</math>, we have the coordinates of <math>E=(12, -\frac{36}{\sqrt7})</math> | ||
| + | |||
| + | Solving for point <math>D</math> (the point on the <math>x</math>-axis between <math>A</math> and <math>E</math>), we get that <math>D=(\frac{264}{31}, 0)</math>. | ||
| + | |||
| + | So now we know six of the critical points: <math>A=(\frac{99}{16}, \frac{55\sqrt7}{16})</math>; <math>B=(0, 0)</math>; <math>C=(24, 0)</math>; <math>D=(\frac{264}{31}, 0)</math>; <math>E=(12, -\frac{36}{\sqrt7})</math>; <math>O=(12, -\frac{4}{\sqrt7})</math>. | ||
| + | |||
| + | We are now ready to add in the circumcircle of <math>\triangle BDE</math>, which has radius <math>\frac{BD\cdot DE\cdot BE}{4[BDE]}</math>. From the above information, <math>BD=\frac{264}{31}</math>, <math>DE=\sqrt{(\frac{108}{31})^2+(\frac{36}{\sqrt7})^2}</math>, and <math>BE=\sqrt{12^2+(\frac{36}{\sqrt7})^2}</math>. | ||
| + | |||
| + | After a bit of simplification we end up with <math>DE=\frac{1152}{31\sqrt7}</math> and <math>BE=\frac{48}{\sqrt7}</math>. | ||
| + | |||
| + | For the area of <math>\triangle BDE</math>, the altitude dropped from vertex <math>E</math> has height <math>\frac{36}{\sqrt7}</math>, and the base <math>\overline{BD}</math> has length <math>\frac{264}{31}</math>, so its area is <math>\frac12\cdot\frac{36}{\sqrt7}\cdot\frac{264}{31}=\frac{4752}{31\sqrt7}</math>. | ||
| + | |||
| + | Thus, <math>\frac{BD\cdot DE\cdot BE}{4[BDE]}=\frac{\tfrac{264}{31}\cdot\tfrac{1152}{31\sqrt7}\cdot\tfrac{48}{\sqrt{7}}}{4\cdot\tfrac{4752}{31\sqrt7}}</math> which after tons of cancellations becomes <math>\frac{768}{31\sqrt7}</math>. | ||
| + | |||
| + | We know from the perpendicular bisector rule that the circumcenter <math>P</math> of <math>\triangle BDE</math> is located directly below the midpoint of <math>\overline{BD}</math> (<math>x</math>-coordinate <math>\frac{132}{31}</math>). | ||
| + | |||
| + | So, the negative <math>y</math>-coordinate of <math>P</math> satisfies <math>(\frac{132}{31})^2+y^2=(\frac{768}{31\sqrt7})^2</math>, and solving gives <math>y=-\frac{684}{31\sqrt7}</math>. Thus, the equation of the circumcircle of <math>\triangle BDE</math> is <math>(x-\frac{132}{31})^2+(y+\frac{684}{31\sqrt7})^2=(\frac{768}{31\sqrt7})^2</math>. | ||
| + | |||
| + | Point <math>F</math> is the intersection of this circle and the line <math>\overline{AB}</math>, which has equation <math>y=\frac{5\sqrt7}{9}x</math>. So, we substitute <math>y=\frac{5\sqrt7}{9}x</math> into the equation of the circle to get <math>(x-\frac{132}{31})^2+(\frac{5\sqrt7}{9}x+\frac{684}{31\sqrt7})^2=(\frac{768}{31\sqrt7})^2</math>. | ||
| + | |||
| + | After simplifying, we have <math>\frac{256}{81}x^2+16x=0</math> (the <math>\frac{768}{31\sqrt7}</math>'s cancel out), whose solutions are <math>x=0</math> and <math>x=-\frac{81}{16}</math>. The first corresponds to the origin, and the second corresponds to point <math>F</math>. Thus the coordinates of <math>F</math> are <math>(-\frac{81}{16}, \frac{5\sqrt7}{9}\cdot\frac{-81}{16})=(-\frac{81}{16}, -\frac{45\sqrt7}{16})</math>. | ||
| + | |||
| + | The coordinates of <math>C</math> are <math>(24, 0)</math>, so <cmath>CF=\sqrt{(24+\frac{81}{16})^2+(\frac{45\sqrt7}{16})^2}=\sqrt{(\frac{465}{16})^2+(\frac{45\sqrt7}{16})^2}=\frac{\sqrt{465^2+(45\sqrt7)^2}}{16}=\frac{\sqrt{(15\cdot 31)^2+(15\cdot 3\sqrt7)^2}}{16}=\frac{15\sqrt{31^2+(3\sqrt7)^2}}{16}=\frac{15\sqrt{961+63}}{16}=\frac{15\sqrt{1024}}{16}=\frac{15}{16}\cdot 32=30.</cmath> | ||
| + | |||
| + | ==Video Solution by Power of Logic(Trig and Power of a point)== | ||
| + | https://youtu.be/tEVbTtJlZjA | ||
| − | + | ~math2718281828459 | |
| − | + | ==See Also== | |
| + | {{AMC12 box|year=2021 Fall|ab=B|num-a=25|num-b=23}} | ||
| − | + | [[Category:Intermediate Geometry Problems]] | |
| + | {{MAA Notice}} | ||
Latest revision as of 11:11, 23 November 2023
Contents
Problem
Triangle ![]() has side lengths
has side lengths ![]() , and
, and ![]() . The bisector of
. The bisector of ![]() intersects
intersects ![]() in point
in point ![]() , and intersects the circumcircle of
, and intersects the circumcircle of ![]() in point
in point ![]() . The circumcircle of
. The circumcircle of ![]() intersects the line
intersects the line ![]() in points
in points ![]() and
and ![]() . What is
. What is ![]() ?
?
![]()
Solution 1 (Reflection)
By the Law of Cosine ![]()
As ![]() is a cyclic quadrilateral,
is a cyclic quadrilateral, ![]() . As
. As ![]() is a cyclic quadrilateral,
is a cyclic quadrilateral, ![]() .
.
![]()
![]() by
by ![]()
Hence, ![]()
By the Law of Cosine ![]()
Note that ![]() is
is ![]() 's reflection over line
's reflection over line ![]() , quadrilateral
, quadrilateral ![]() is a kite symmetrical by line
is a kite symmetrical by line ![]() ,
, ![]() .
.
Solution 2 (Olympiad Solution using Spiral Similarity)
Construct the ![]() -antipode,
-antipode, ![]() . Notice
. Notice ![]() by spiral similarity at
by spiral similarity at ![]() , thus
, thus ![]() . Let
. Let ![]() ; by symmetry
; by symmetry ![]() as well and
as well and ![]() from Law of Cosines in
from Law of Cosines in ![]() , so by Law of Cosines in
, so by Law of Cosines in ![]() we have
we have ![]() from which
from which ![]() . Now,
. Now, ![]() .
.
Solution 3
Claim: ![]()
Proof: Note that ![]() and
and ![]() meaning that our claim is true by AA similarity.
meaning that our claim is true by AA similarity.
Because of this similarity, we have that ![]() by Power of a Point. Thus,
by Power of a Point. Thus, ![]()
Two solution methods follow from here.
Solution 3.1 (Stewart's theorem)
Applying Stewart's theorem on ![]() with cevian
with cevian ![]() using the directed lengths
using the directed lengths ![]() and
and ![]() , we obtain
, we obtain ![]() so
so ![]() .
.
Solution 3.2 (Double Cosine Law)
Note that ![]() so we may plug into Law of Cosines to find the angle's cosine:
so we may plug into Law of Cosines to find the angle's cosine: ![]()
So, we observe that we can use Law of Cosines again to find ![]() :
: ![]() both ways.
both ways.
- Kevinmathz
Solution 4
This solution is based on this figure: 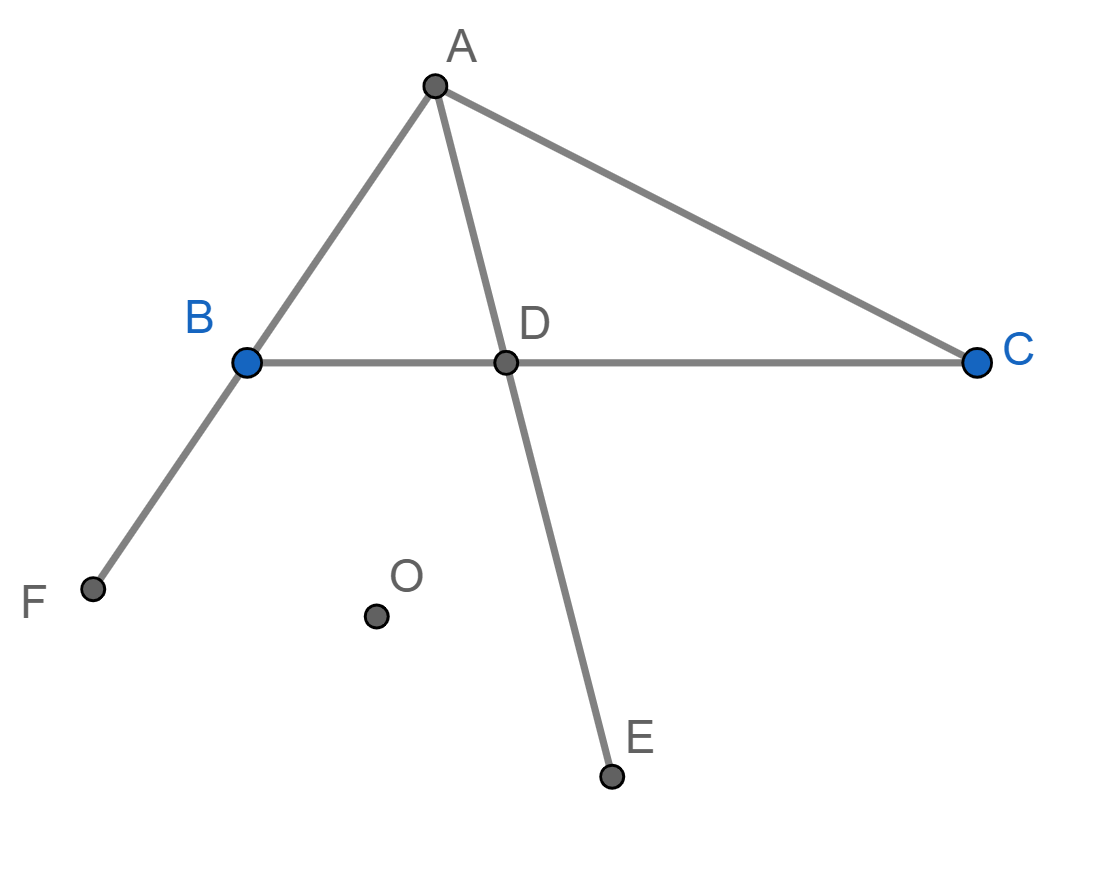
Denote by ![]() the circumcenter of
the circumcenter of ![]() .
Denote by
.
Denote by ![]() the circumradius of
the circumradius of ![]() .
.
In ![]() , following from the law of cosines, we have
, following from the law of cosines, we have
![]() For
For ![]() , we have
, we have
 The fourth equality follows from the property that
The fourth equality follows from the property that ![]() ,
, ![]() ,
, ![]() are concyclic.
The fifth and the ninth equalities follow from the property that
are concyclic.
The fifth and the ninth equalities follow from the property that ![]() ,
, ![]() ,
, ![]() ,
, ![]() are concyclic.
are concyclic.
Because ![]() bisects
bisects ![]() , following from the angle bisector theorem, we have
, following from the angle bisector theorem, we have
![]() Hence,
Hence, ![]() .
.
In ![]() , following from the law of cosines, we have
, following from the law of cosines, we have
 and
and
 Hence,
Hence, ![]() and
and ![]() .
Hence,
.
Hence, ![]() .
.
Now, we are ready to compute ![]() whose expression is given in Equation (2).
We get
whose expression is given in Equation (2).
We get ![]() .
.
Now, we can compute ![]() whose expression is given in Equation (1).
We have
whose expression is given in Equation (1).
We have ![]() .
.
Therefore, the answer is ![]() .
.
~Steven Chen (www.professorchenedu.com)
Solution 5
Denote ![]() and
and ![]() . Note that by Heron's formula the area of
. Note that by Heron's formula the area of ![]() is
is ![]() so the
so the ![]() -coordinate of
-coordinate of ![]() (height of
(height of ![]() above the
above the ![]() -axis) is easily computed by the base-height formula as
-axis) is easily computed by the base-height formula as ![]() .
.
Now, since ![]() , the
, the ![]() -coordinate of
-coordinate of ![]() satisfies
satisfies ![]() and solving gives
and solving gives ![]() .
.
The circumcircle of ![]() has radius
has radius ![]() . We know by the perpendicular bisector rule that the circumcenter
. We know by the perpendicular bisector rule that the circumcenter ![]() is located directly below the midpoint of
is located directly below the midpoint of ![]() (
(![]() -coordinate
-coordinate ![]() ).
).
So, the negative ![]() coordinate of
coordinate of ![]() satisfies
satisfies ![]() and solving gives
and solving gives ![]() .
.
It's also clear that point ![]() is going to be located directly below
is going to be located directly below ![]() on the circle, because the angle bisector intersects the circumcircle at the midpoint of the arc (Fact 5). Since the radius of the circle is
on the circle, because the angle bisector intersects the circumcircle at the midpoint of the arc (Fact 5). Since the radius of the circle is ![]() , we have the coordinates of
, we have the coordinates of ![]()
Solving for point ![]() (the point on the
(the point on the ![]() -axis between
-axis between ![]() and
and ![]() ), we get that
), we get that ![]() .
.
So now we know six of the critical points: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
We are now ready to add in the circumcircle of ![]() , which has radius
, which has radius ![]() . From the above information,
. From the above information, ![]() ,
,  , and
, and  .
.
After a bit of simplification we end up with ![]() and
and ![]() .
.
For the area of ![]() , the altitude dropped from vertex
, the altitude dropped from vertex ![]() has height
has height ![]() , and the base
, and the base ![]() has length
has length ![]() , so its area is
, so its area is ![]() .
.
Thus, ![$\frac{BD\cdot DE\cdot BE}{4[BDE]}=\frac{\tfrac{264}{31}\cdot\tfrac{1152}{31\sqrt7}\cdot\tfrac{48}{\sqrt{7}}}{4\cdot\tfrac{4752}{31\sqrt7}}$](http://latex.artofproblemsolving.com/2/7/6/276b62dd90421d5875bf906797ba0982b867f94c.png) which after tons of cancellations becomes
which after tons of cancellations becomes ![]() .
.
We know from the perpendicular bisector rule that the circumcenter ![]() of
of ![]() is located directly below the midpoint of
is located directly below the midpoint of ![]() (
(![]() -coordinate
-coordinate ![]() ).
).
So, the negative ![]() -coordinate of
-coordinate of ![]() satisfies
satisfies ![]() , and solving gives
, and solving gives ![]() . Thus, the equation of the circumcircle of
. Thus, the equation of the circumcircle of ![]() is
is ![]() .
.
Point ![]() is the intersection of this circle and the line
is the intersection of this circle and the line ![]() , which has equation
, which has equation ![]() . So, we substitute
. So, we substitute ![]() into the equation of the circle to get
into the equation of the circle to get ![]() .
.
After simplifying, we have ![]() (the
(the ![]() 's cancel out), whose solutions are
's cancel out), whose solutions are ![]() and
and ![]() . The first corresponds to the origin, and the second corresponds to point
. The first corresponds to the origin, and the second corresponds to point ![]() . Thus the coordinates of
. Thus the coordinates of ![]() are
are ![]() .
.
The coordinates of ![]() are
are ![]() , so
, so ![\[CF=\sqrt{(24+\frac{81}{16})^2+(\frac{45\sqrt7}{16})^2}=\sqrt{(\frac{465}{16})^2+(\frac{45\sqrt7}{16})^2}=\frac{\sqrt{465^2+(45\sqrt7)^2}}{16}=\frac{\sqrt{(15\cdot 31)^2+(15\cdot 3\sqrt7)^2}}{16}=\frac{15\sqrt{31^2+(3\sqrt7)^2}}{16}=\frac{15\sqrt{961+63}}{16}=\frac{15\sqrt{1024}}{16}=\frac{15}{16}\cdot 32=30.\]](http://latex.artofproblemsolving.com/3/0/5/3059ce15c6ee11d5471b72969d6bb6ab76391377.png)
Video Solution by Power of Logic(Trig and Power of a point)
~math2718281828459
See Also
| 2021 Fall AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 23 |
Followed by Problem 25 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.