PQ = r and 6 more conditions

Art of Problem Solving

AoPS Online

High School Olympiads Regional, national, and international math olympiads

Regional, national, and international math olympiads

3 M G

BBookmark VNew Topic kLocked

High School Olympiads Regional, national, and international math olympiads

Regional, national, and international math olympiads

3 M G

BBookmark VNew Topic kLocked

B

No tags match your search

M

PQ = r and 6 more conditions

G H J

Reveal topic tags

L

G H BBookmark kLocked kLocked NReply

Source: 2023 ISL G2

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

294 posts

#1 h Jul 17, 2024, 12:00 PM • 4 Y

Y by Rounak_iitr, OronSH, peace09, ItsBesi

Let $ABC$ be a triangle with $AC > BC,$ let $\omega$ be the circumcircle of $\triangle ABC,$ and let $r$ be its radius. Point $P$ is chosen on $\overline{AC}$ such taht $BC=CP,$ and point $S$ is the foot of the perpendicular from $P$ to $\overline{AB}$ . Ray $BP$ mets $\omega$ again at $D$ . Point $Q$ is chosen on line $SP$ such that $PQ = r$ and $S,P,Q$ lie on a line in that order. Finally, let $E$ be a point satisfying $\overline{AE} \perp \overline{CQ}$ and $\overline{BE} \perp \overline{DQ}$ . Prove that $E$ lies on $\omega$ .

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

1595 posts

#2 h Jul 17, 2024, 12:04 PM • 3 Y

Y by peace09, OronSH, BorivojeGuzic123

Solution

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

1748 posts

OronSH

#3 h Jul 17, 2024, 12:06 PM • 2 Y

Y by peace09, ehuseyinyigit

The main idea is that $Q$ is the circumcenter of $\triangle PCD.$

First let $H$ be the midpoint of arc $AB$ not containing $C$ on $(ABC).$ Then $CH$ bisects $\angle BCP,$ but $\triangle BCP$ is isosceles so $CH\perp BD.$ Similarly $DH\perp AC$ since $\triangle BCP\sim\triangle ADP$ from $ABCD$ cyclic. Thus $H$ is the orthocenter of $\triangle PCD,$ so the $(ABCDH)$ and $(PDC)$ are congruent.

Next we show $SP$ passes through the circumcenter of $\triangle PCD.$ This is because there exists an negative inversion at $P$ swapping $A$ and $C$ and also swapping $B$ and $D.$ Then $S$ is sent to the antipode of $P$ on $(PCD),$ so $SP$ passes through this point and thus passes through the center of $(PCD).$

Together these imply that $Q$ is the center of $(PCD).$ To finish, we have $\begin{align*}\measuredangle AEB&=\measuredangle(AE,QC)+\measuredangle CQD+\measuredangle(QD,BE)=90+90+\measuredangle CQD\\&=\measuredangle CQD=2\measuredangle CPD=2\measuredangle CPB=\measuredangle CPB+\measuredangle PBC=\measuredangle PCB\\&=\measuredangle ACB\end{align*}$ so $A,B,C,E$ are concyclic.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

821 posts

#4 h Jul 17, 2024, 12:07 PM • 1 Y

Y by peace09

Let $E$ be on $\omega$ such that $CB=CE$ .

Claim: $DPCO$ is cyclic with center $Q$ .
Proof. The circumradius condition and spiral similarity at $C$ gives $CQ=QO=QP$ . Then, $\measuredangle CPD=2\measuredangle CBP =2\measuredangle CBD =\measuredangle COD$ as desired. $\blacksquare$

Now, note that $P$ is the incenter of $ABE$ by fact $5$ . Thus $180^{\circ} -\angle(BE,DQ)=\angle EBP+\angle DPQ=\angle PBA+\angle DPQ=\angle PBS+\angle SPB=90 ^{\circ}$ and $180^{\circ} - \angle(AE,CQ)=\angle EAC+\angle QCA=\angle APS+\angle SAP=90^{\circ}$ concluding.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

302 posts

#5 h Jul 17, 2024, 12:50 PM

Y by

It suffices to show that $\angle DQC = 180^\circ - \angle ACB$ .
In $\Delta ABC$ , write $\angle A = \alpha, \angle B = \beta, \angle C = \gamma$ .
Note that $\Delta OBC \cong \Delta QPC$ , so by spiral similarity we have $\Delta BCP \sim \Delta OCQ$ .
Let $R=AO \cap SP$ .

Since $\angle DAR = 90^\circ - \angle DBA$ and $\angle DPR = 180^\circ - \angle BPS = 180^\circ - (90^\circ - \angle DBA) = 90^\circ + \angle DBA$ , we have that $(ADPR)$ is concyclic.
Also,
$\angle RDO = \angle ADO - \angle ADR = 90^\circ - \angle DBA - \angle CPQ = 90^\circ - (\beta - (90^\circ - \frac{\gamma}{2})) - (90^\circ - \alpha) = 90^\circ + \alpha - \beta - \frac{\gamma}{2} = \frac{3}{2}\alpha - \frac{\beta}{2}$
and $\angle RQO = \angle CQP - \angle CQO = 2\alpha - (90^\circ - \frac{\gamma}{2}) = \frac{3}{2}\alpha - \frac{\beta}{2} = \angle RDO$ , so $(DOQR)$ is concyclic.
Thus $\angle DQC = \angle DQO + \angle CQO = (180^\circ - \angle DRO) + \angle CBP = \angle CPB + \angle CBP = 180^\circ - \angle ACB$ , hence proved.

Attachments:

This post has been edited 1 time. Last edited by Aiden-1089, Jul 17, 2024, 4:00 PM

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

407 posts

#6 h Jul 17, 2024, 1:39 PM • 1 Y

Y by isomoBela

Note that $\angle DAC = \angle DBC = \angle CPB = \angle DPA$ , so $DP = DA$ . Now if $L$ is the midpoint of the arc $AB$ in $\omega$ , not containing $C$ , then $CL$ and $DL$ are angle bisectors of $\angle BCP$ and $\angle ADP$ , so $LADP$ and $LBCP$ are kites. Hence $LB = LP = LA$ and $CP\perp DL$ , $DP\perp CL$ . Therefore $P$ is the orthocenter of $\triangle CDL$ , and points $B$ and $A$ are the reflections of $P$ over $CL$ and $DL$ , respectively.
Working with complex numbers and $\omega$ as the unit circle, the above translates to $p = c+d+\ell$ , $a = -\frac{d\ell}{c}$ , $b = -\frac{c\ell}{d}$ . Additionally, if $O$ is the circumcenter of $\omega$ , then $PS\perp AB \perp OL$ and $OL = r = PQ$ , so $PQOL$ is a parallelogram. Therefore, $q = p - \ell = c+d$ . Regarding the condition of $E$ lying on $\omega$ , this is equivalent to $\angle EAC = \angle EBC$ , but as $EA\perp CQ$ and $EB \perp DQ$ , we have:
$\angle EAC - \angle EBC = (90^{\circ} - \angle PCQ) - (\angle DBC - (90^{\circ} - \angle QDP)) = 180^{\circ} - \angle PCQ - \angle DBC - \angle QDP.$ However, note that $\frac{p-c}{q-c}\cdot\frac{d-b}{c-b}\cdot\frac{q-d}{p-d} = \frac{d+\ell}{d}\cdot\frac{d+\frac{c\ell}{d}}{c+\frac{c\ell}{d}} \cdot \frac{c}{c+\ell} = \frac{d^2+c\ell}{d(c+\ell)}$ is real, so the solution is complete.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

Mahdi_Mashayekhi

698 posts

Mahdi_Mashayekhi

#7 h Jul 17, 2024, 2:15 PM

Y by

Note that $\frac{BC}{\sin{A}} = \frac{PC}{\sin{PDC}}$ so $R_{ABC} = R_{DPC} = r$ . Now since $PQ = r$ and $\angle QPC = \angle APS = 90 - \angle A = 90 - \angle PDC$ we have that $Q$ is center of $DPC$ . Let $AE$ meet $CQ$ at $X$ and $BE$ meet $DQ$ at $Y$ . $\angle AEB = \angle XQY = 180 - \angle DQC = 180 - (360 - 2(180 - \angle BPC)) = 180 - 2\angle BPC = \angle C$ so $E$ lies on $\omega$ .

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

9 posts

teoira

#8 h Jul 17, 2024, 3:13 PM

Y by

Step-by-step solution for 8th graders: https://dgrozev.wordpress.com/2024/07/17/g2-from-imo23-shortlist/

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

blueberryfaygo_55

340 posts

blueberryfaygo_55

#9 h Jul 17, 2024, 3:50 PM • 1 Y

Y by megarnie

Claim. $\Delta QPC = \Delta OBC$ and $\Delta QDP = \Delta ODA$ .
Proof. We know that $PC=BC$ and $PQ = r = OB$ . By angle chasing, we have $\begin{align*} \angle QPC &= \angle APS \\ &= 90^{\circ} - \angle SAP \\ &= 90^{\circ} - \angle BAC \\ &= 90^{\circ} - \dfrac{\angle BOC}{2} \\ &= 90^{\circ} - \dfrac{180^{\circ} - 2 \angle OBC}{2} \\ &= \angle OBC \end{align*}$ and the first part of the claim follows by Side-Angle-Side congruence. Then, note that $\begin{align*} \angle DAP &= \angle DAC \\ &= \angle DBC \\ &= \angle BPC \\ &= \angle APD \end{align*}$ so $\Delta DAP$ is isoceles and $DA = DP$ . We also have $\begin{align*} \angle DPQ &= \angle BPS \\ &= 90^{\circ} - \angle PBS \\ &= 90^{\circ} - \angle DBA \\ &= 90^{\circ} - \dfrac{\angle AOD}{2} \\ &= 90^{\circ} - \dfrac{180^{\circ} - 2 \angle OAD}{2} \\ &= \angle OAD \end{align*}$ and the second part of the claim follows by Side-Angle-Side congruence. $\blacksquare$

Now, we finish the problem by angle chasing to show that $AECB$ is cyclic, which implies the result. First note that $EYQX$ is cyclic since $\angle EYQ = \angle EXQ = 90^{\circ}$ . Indeed, we have $\begin{align*} \angle BEY &= \angle XQC \\ &= \angle DQC \\ &= \angle DQP + \angle PQC \\ &= \angle DOA + \angle BOC \\ &= 2 (\angle ABD + \angle BAC) \\ &= 2 \angle BPC \\ &= 180^{\circ} - \angle ACB \end{align*}$ but $\angle BEY = 180^{\circ} - \angle AEB$ , so $\angle ACB = \angle AEB$ , as desired. $\blacksquare$

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

341 posts

#10 h Jul 17, 2024, 4:01 PM

Y by

Clearly, $\angle CPQ=90^\circ-\angle A$ . By $SAS$ congruence, if $O$ is the circumcenter, $\triangle CPQ\cong \triangle CBO$ . Thus $PQ=QC$ . Let $F$ be the point on $(ABC)$ such $DC=CF$ . Clearly $OC$ is a line through two centres of circles, hence it bisects $\angle FCD$ . But, clearly, $\measuredangle DOC=2\measuredangle DBC=\measuredangle ACB$ . By isosceles $\triangle DOC$ , $\measuredangle DCO=\frac{\measuredangle ACB}{2}$ . By symmetry, $\measuredangle DCF=\measuredangle ACB$ . Now consider the rotation by $\angle C$ degrees. Clearly, $O\rightarrow Q, F\rightarrow D, B\rightarrow P$ . Hence $OF=OC$ implies $QD=QC$ . Thus $PQ=QC=QD$ imples $Q$ is the circumcenter of $\triangle PCD$ .

Angle chasing, as right angles obviously imply cyclic,
$\measuredangle(AE,EB)=\measuredangle(CQ,DQ)=2\measuredangle(CP,PD)-180^\circ=180^\circ-180^\circ-\angle C=\measuredangle(AC,CB)$ We are done by Bowtie.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

302 posts

#11 h Jul 17, 2024, 4:09 PM

Y by

GrantStar wrote:

Let $E$ be on $\omega$ such that $CB=CE$ .

Claim: $DPCO$ is cyclic with center $Q$ .
Proof. The circumradius condition and spiral similarity at $C$ gives $CQ=QO=QP$ . Then, $\measuredangle CPD=2\measuredangle CBP =2\measuredangle CBD =\measuredangle COD$ as desired. $\blacksquare$

Now, note that $P$ is the incenter of $ABE$ by fact $5$ . Thus $180^{\circ} -\angle(BE,DQ)=\angle EBP+\angle DPQ=\angle PBA+\angle DPQ=\angle PBS+\angle SPB=90 ^{\circ}$ and $180^{\circ} - \angle(AE,CQ)=\angle EAC+\angle QCA=\angle APS+\angle SAP=90^{\circ}$ concluding.

I think this is wrong, $DPCO$ doesn't seem to be concyclic. Where did you get $CQ=QO$ ?

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

821 posts

#12 h Jul 17, 2024, 5:28 PM

Y by

Oops wait you’re right I forgot my solution that I submitted. Once you get CQ=QP you can angle chase to identify Q as the circumcenter of BCD. I will change this later

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

1756 posts

#13 h Jul 17, 2024, 5:37 PM

Y by

Beautiful!

Claim: $Q$ is the circumcenter of $\triangle DPC.$
Proof: There are two steps to proving this claim. The first is showing that the circumradius of $\triangle DPC$ is $r.$ This is easy enough: if $r'$ is the circumradius of $\triangle DPC,$ the Law of Sines implies that $r' = \frac{PC}{2 \sin \angle PDC} = \frac{BC}{2 \sin \angle BDC} = r.$ The second step is showing that $PQ$ passes through the circumcenter of $\triangle PCD,$ which follows since $PQ \perp AB,$ $ABCD$ is cyclic, and the orthocenter and circumcenter are isogonal conjugates in a triangle. These conditions pinpoint $Q$ down to one place, namely the circumcenter of $\triangle DPC,$ as claimed.

Now let $O$ be the circumcenter of $\triangle ABC.$ Because $\triangle DPC$ has the same radius as $\omega,$ we see that $O$ and $Q$ are reflections across $CD.$ Furthermore, since $CO = OD$ and $CQ = QD,$ we see that $OCQD$ is a rhombus and thus a parallelogram. Hence $AE \perp DO$ and $BE \perp CO.$ Therefore, we need to show that there exists a point $E'$ on $\omega$ such that $AD = DE'$ and $BC = CE'.$ This is equivalent to showing that $f(AD) + f(BC) = f(CD),$ where $f$ measures the length of an arc. Indeed, $\angle ABD + \angle BAC = \angle BAP + \angle ABP = \angle BPC = \angle PBC = \angle DBC,$ and we are done. why did \overarc stop working

This post has been edited 2 times. Last edited by EpicBird08, Jul 17, 2024, 6:35 PM

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

779 posts

#14 h Jul 18, 2024, 3:57 AM

Y by

Different solution:

Let $M$ be the arc midpoint of arc $BCA.$

$\textbf{Claim: }$ $CMDP$ is a parallelogram.
$\emph{Proof: }$ We have $\angle MCA=\angle MBA=\tfrac{180^\circ-\angle C}{2}=\angle CPD,$ so $\overline{CM}\parallel\overline{PD}.$ Moreover, since $CMDB$ is an isosceles trapezoid, $MD=CB=CP.$ $\blacksquare$

$\textbf{Claim:}$ $OMQP$ is a parallelogram.
$\emph{Proof:}$ Both $\overline{OM}$ and $\overline{PQ}$ are perpendicular to $\overline{AB},$ so $\overline{OM}\parallel\overline{PQ}.$ Moreover, $PQ=r=OM.$ $\blacksquare$

These two claims together imply that $CODQ$ is a parallelogram. Hence, $\angle CQD=\angle COD=180^\circ-\angle C,$ which (by a phantom point argument) suffices.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

920 posts

#15 h Jul 19, 2024, 1:25 AM

Y by

Let $O$ be the center of $(ABC)$ . Redefine $E$ as the reflection of $P$ about $CD$ and $Q$ as the reflection of $O$ about $CD$ . We show they satisfy the stated properties.

Claim: $E\in (ABC)$
$\angle DEC=180^{\circ}-\angle BPC=180^{\circ}-\angle PBC$
Claim: $PQ=r$
Just reflect about $CD$ .
Claim: $PQ\perp AB$
$\angle BPQ-\angle ABP=180^{\circ}-\angle BDQ-\angle ABP=90^{\circ}-\angle ABP-\angle CAB+\angle DBC=90^{\circ}$
Claim: $AE\perp CQ$
Simply, $AX\perp OD\parallel CQ$ .
Claim: $BE\perp DQ$
By simple angle chase, $BX\perp OC\parallel DQ$ .

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

32 posts

#16 h Jul 19, 2024, 2:51 PM • 1 Y

Y by sami1618

Proposed by Mahdi Etesamifard, Iran

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

24 posts

#17 h Jul 20, 2024, 11:17 AM

Y by

Define $E$ as the intersection between $\omega$ and the line perpendicular to $DQ$ , and define $L$ as the intersection between $BE$ and $DQ$ . Define $K$ as the foot of the perpendicular from $CQ$ to $E$ . It is sufficient to prove that $A$ , $E$ , and $K$ are collinear.

$\angle CPQ = \angle APS = 90 - \angle SAP = 90 - \angle BAC = \angle OBC$ , and since $PQ=r=OB$ and $BC=PC$ , so $\Delta COB \sim \Delta CPQ$ , in a spiral similarity centered at $C$ . Thus $\Delta CPB \sim \Delta CQO$ . Moreover, $\angle COD = 2 \angle CBD = 2 \angle CBP = 180 - \angle BCP = 180 - \angle QCO = 2\angle COQ$ . Thus, $\angle QOC = \angle DOQ$ , and since $DO=OC$ , $DOQC$ is, thus, a parallelogram.
We finish with an angle chase:
$\angle BEK=\angle LEK = 180 - \angle LQK = 180 - \angle OCQ = 180- \angle BCP = 180- \angle BCA = 180 - \angle BEA$ .
Therefore, $K, E, A$ are collinear, which finishes up the problem.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

892 posts

#18 h Jul 20, 2024, 3:40 PM

Y by

Define $E$ as the point on $(ABC)$ with $\angle EAC = \angle BAC$ .

Because $PQ = BO, PC = BC, \angle OBC = 90 - \angle BAC =\angle APS = \angle QPC$ , $QPC \cong OBC$ . Additionally, $\angle PDC = \angle BAC = 2 \angle BOC = 2 \angle PQC$ gives $Q$ is the circumcenter of $PDC$ . Lastly, $\angle ABE = \angle B -\angle A = 2 \angle ABP$ . Therefore, $\angle BDQ + \angle DBE = 90 - \angle DCP + \angle ABD = 90$ which shows $EB \perp DQ$ and $\angle EAC + \angle QCA = \angle A + 90 - \angle A = 90$ which shows $AE \perp CQ$ . $\square$

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

1391 posts

#19 h Jul 21, 2024, 12:30 AM

Y by

Solution

This post has been edited 1 time. Last edited by VicKmath7, Jul 21, 2024, 10:45 AM

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

173 posts

#20 h Jul 22, 2024, 2:07 AM

Y by

Let $R$ be the circumradius of $\triangle CPD$ . By law of sines, we then get
$2R = \frac{CP}{\sin \angle PDC} = \frac{CB}{\sin \angle BDC} = 2r,$ so $R = r = PQ$ . Moreover, $\angle QPD = \angle BPS = 90^\circ - \angle PBS = 90^\circ - \angle DCP$ , so it follows that $Q$ is the circumcenter of $\triangle PDC$ . Therefore,
$\measuredangle AEB = \measuredangle CQD = 2\measuredangle CPD = \measuredangle CPB + \measuredangle PBC = \measuredangle ACB,$ so $E$ lies on $(ABC)$ .

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

1619 posts

#21 h Jul 22, 2024, 2:26 PM

Y by

Let $O$ be center of $\omega$ . We have $(PC, PQ) \equiv (PA, PS) \equiv \dfrac{\pi}{2} + (AC, AB) \equiv (BC, BO) \pmod \pi$ . Combine with $PQ = OB = r$ and $CP = BC,$ we have $\triangle OBC \cong \triangle QPC$ . Then $QP = QC = r$ and $(DP, DC) \equiv \dfrac{1}{2} (\overrightarrow{OB}, \overrightarrow{OC}) \equiv \dfrac{1}{2} (\overrightarrow{QP}, \overrightarrow{QC}) \pmod \pi$ . So $D \in (Q, r)$ . Hence $(EA, EB) \equiv (QC, QD) \equiv 2(PC, PD) \equiv 2(PC, PB) \equiv (CA, CB) \pmod \pi$ of $E \in \omega$

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

347 posts

#22 h Jul 22, 2024, 4:29 PM

Y by

avisioner wrote:

Let $ABC$ be a triangle with $AC > BC,$ let $\omega$ be the circumcircle of $\triangle ABC,$ and let $r$ be its radius. Point $P$ is chosen on $\overline{AC}$ such taht $BC=CP,$ and point $S$ is the foot of the perpendicular from $P$ to $\overline{AB}$ . Ray $BP$ mets $\omega$ again at $D$ . Point $Q$ is chosen on line $SP$ such that $PQ = r$ and $S,P,Q$ lie on a line in that order. Finally, let $E$ be a point satisfying $\overline{AE} \perp \overline{CQ}$ and $\overline{BE} \perp \overline{DQ}$ . Prove that $E$ lies on $\omega$ .

$\color{blue}\boxed{\textbf{Proof:}}$
$\color{blue}\rule{24cm}{0.3pt}$
Lemma: $\angle ACB+\angle DQC=180$
Proof 1
Proof 2
Let $E'\equiv AE\cap CQ , T\equiv DQ\cap BC$
$\angle E'BC=\angle E'AC=90-\angle QCA=90-(\angle QCB-\angle ACB)=90-(\angle TQC+\angle QTC-\angle ACB)=90-\angle QTC\Rightarrow BE'\perp DQ \Rightarrow E'\equiv E_\blacksquare$
$\color{blue}\rule{24cm}{0.3pt}$

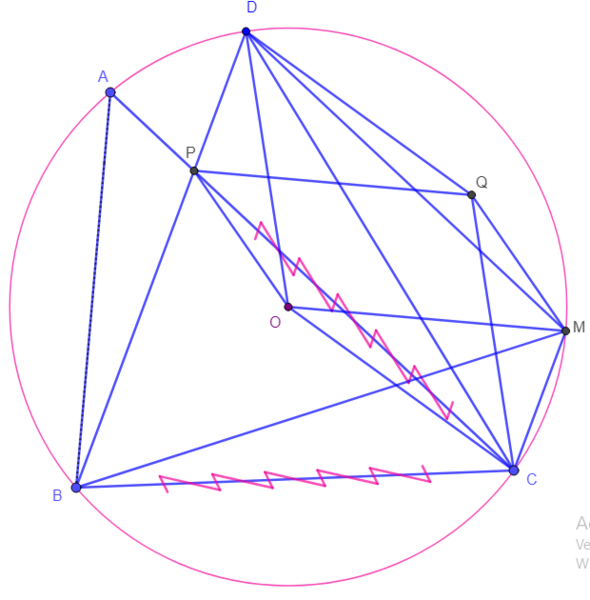
https://wiki-images.artofproblemsolving.com//thumb/8/8a/ISL_2023_G2.PNG/590px-ISL_2023_G2.PNG

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

4 posts

#23 h Jul 22, 2024, 5:00 PM

Y by

Let $BE \cap DQ = G$ and $O$ be the center of $\omega$ . Note that $\angle OAD = 90^\circ - \angle ABD = \angle DPQ$ . Also, $\angle DAP = \angle DBC = \angle APD$ so $AD = DP$ . Therefore, $\triangle DAO \cong \triangle DPQ$ and so $\triangle DAP \cong \triangle DOG$ . This gives $DQ = PQ$ and $\angle DQP = \angle AOD = 2\angle ABD = 2\angle PCD$ , implying $Q$ is the center of $(PCD)$ and so $DQ = CQ$ . Thus, we have $DOCQ$ being a rhombus. Lastly, note that $\angle AEB = 180^\circ - 2\angle DQO = 180^\circ - 2\angle BPC = \angle ACB$ . Hence, $E$ lies on $(ABC)$ .

Attachments:

This post has been edited 1 time. Last edited by iced_tea, Jul 22, 2024, 5:13 PM

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

9 posts

#24 h Jul 25, 2024, 9:02 PM

Y by

My first G2 !

Let us introduce $O$ the center of the circumcircle. Notice that the angles $\angle APS, \angle SPB, \angle BPC$ can be chased easily.
The key point to find the other angles is to notice that $BOC$ is similar to $PQC$ (one angle and two sides), and $PQD$ is similar to $AOD$ (here, we would want to use again the one angle/two sides condition, but for that we need $AD = PD$ . However, remark that $\angle DAP = \angle DBC = \angle PBC = \angle BPC = \angle APD$ , as wished. ). The similarity of these triangles give access to many angles, enough to calculate $\angle DBE$ and $\angle DAE$ , and see that they are equal. Hence $A,D,E,B$ are concyclic which means that $E \in \omega \huge{\blacksquare}$ .

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

cursed_tangent1434

656 posts

cursed_tangent1434

#25 h Aug 20, 2024, 3:40 PM

Y by

Pretty easy. Funnily, our national Olympiad also had a problem which involved circles with equal circumradii so I was prepared for the weird condition here. Let $O$ denote the circumcenter of $\triangle ABC$ , and let $R$ and $T$ be the feet of the perpendiculars from $B$ to $\overline{DQ}$ and from $A$ to $\overline{CQ}$ .

$[asy] /* Converted from GeoGebra by User:Azjps using Evan's magic cleaner https://github.com/vEnhance/dotfiles/blob/main/py-scripts/export-ggb-clean-asy.py */ real xmin = 2.5, xmax = 20.5, ymin = -9., ymax = 6.; pen pri; pri=RGB(24, 105, 174); pen sec; sec=RGB(217, 165, 179); pen tri; tri=RGB(126, 123, 235); pen fil=invisible; pen sfil=invisible; pen tfil=invisible; pair O = (9.,-2.); pair A = (5.8,3.56); pair B = (4.,-6.); pair C = (14.00935,-6.00748); pair P = (7.49139,1.58879); pair S = (5.49946,1.96383); pair D = (8.79012,4.41167); pair Q = (13.79180,0.40034); pair T = (13.67545,3.82738); pair R = (10.95662,2.67414); pair E = (11.83131,3.76477); import graph; size(10cm); pen fueaev = rgb(0.95686,0.91764,0.89803); pen zzttqq = rgb(0.6,0.2,0.); pen fsfsff = rgb(0.94901,0.94901,1.); draw(A--B--C--cycle); filldraw(circle(Q, 6.41152),white+0.1*pri, pri); draw(circle(O, 6.41510), linewidth(0.6)); draw(A--B, linewidth(0.6) + zzttqq); draw(B--C, linewidth(0.6) + zzttqq); draw(C--A, linewidth(0.6) + zzttqq); draw((xmin, -0.18828*xmin + 2.99930)--(xmax, -0.18828*xmax + 2.99930), linewidth(0.6) + linetype("2 2")); draw(B--D, linewidth(0.6)); draw(C--T, linewidth(0.6) + dotted); draw(T--A, linewidth(0.6) + dotted); draw(B--E, linewidth(0.6) + dotted); dot("$O$", O, dir((8.000, 20.000))); dot("$A$", A, dir((8.000, 20.000))); dot("$B$", B, dir(210)); dot("$C$", C, dir(320)); dot("$P$", P, dir(30)); dot("$S$", S, dir(40)); dot("$D$", D, dir(100)); dot("$Q$", Q, dir((8.820, 15.966))); dot("$T$", T, dir((8.455, 15.262))); dot("$R$", R, dir(0)); dot("$E$", E, dir((8.869, 15.523))); [/asy]$
Due to the right angles it is immediately clear that $ERQT$ is cyclic. Thus, it suffices to show the following key claim.

Claim : $Q$ is the circumcenter of $\triangle DPC$ .

Proof : Let $\Gamma$ denote the circumcenter of $\triangle DPC$ and let $Q'$ be its circumcenter. First note that,
$2\measuredangle Q'PC = \measuredangle PQ'C = 2\measuredangle PDC = 2\measuredangle BDC = 2\measuredangle BAC$ so, $\measuredangle Q'PC = 90 + \measuredangle BAC$ from which it is clear that $Q'P \perp AB$ . So, $Q'$ lies on the line $\overline{SP}$ .

Further, note that
$\measuredangle DPC = \measuredangle BPC = \measuredangle CBP = \measuredangle CBD$ so the segment $DC$ must subtend equal angles at the centers of $\omega$ and $\Gamma$ . This then implies that the circles $\omega$ and $\Gamma$ are congruent, and in particular they have the same circumradius. Thus, $Q'P = r = QP$ , which implies that $Q'\equiv Q$ , implying the claim.

Note that $DO=OC = r = QC=QD$ so it follows that $DOCQ$ is a rhombus. Now, we are left with a simple angle chase,
$\measuredangle BEA = \measuredangle REA = \measuredangle RQT = \measuredangle DQT = \measuredangle COD = 2\measuredangle CBD = \measuredangle BCP = \measuredangle BCA$ which implies that $E$ indeed lies on $\omega$ as desired.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

30 posts

#26 h Sep 4, 2024, 11:34 AM • 1 Y

Y by Anancibedih

Let $K$ be the foot of $A$ to $QC$ . Let $AK$ intersects with the circumcircle of $\triangle{ABC}$ at $E$ at the second time. And let $O$ be the center of $(ABC)$ . We are going to prove $BE \perp DQ$ to finish the problem. (So our $E$ would be same as the $E$ in the problem.)

Claim1: $\triangle BOC \cong \triangle PQC$ .
Proof: Easily conclude that $\angle QPC = 90-\angle A = \angle OBC$ .
$PQ = OB$ and $PC = BC$ . $\square$

Claim 2: $OC \perp EB$ .
Proof: By Claim 1, $\angle PQC = 2\angle A$ .
Also $(ASQK)$ , hence $\angle SAK = 2\angle A \implies \angle PAE = \angle A$
That means $BC = CE$ . $\square$

Now, we know that $DO = CQ$ . If we prove $DO || QC$
$\implies DOQC$ is paralellogram $\implies DQ || OC \implies DQ \perp EB$ and we would be done.

Finishing Claim: $DO || QC$ .
Proof: $DO || QC \iff DO \perp AE \iff AD = DE$ . So we are going to prove the arcs $AD$ and $DE$ are equal.
$\text{arc}(AE) = 360 - 4\angle A - 2\angle C = 2(\angle B - \angle A)$
$\text{arc}(AD) = 2\angle ABD = 2(\angle B - (90 - \frac{\angle C}{2})) = \angle B - \angle A$
$\text{arc}(AE) = 2.\text{arc}(AD)$
$\text{arc}(AD) = \text{arc}(DE)$
$\blacksquare$

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

481 posts

#27 h Sep 26, 2024, 8:14 PM • 2 Y

Y by HACK_IN_MATHS, SilverBlaze_SY

Solved with SilverBlaze_SY.

$[asy] /* Converted from GeoGebra by User:Azjps using Evan's magic cleaner https://github.com/vEnhance/dotfiles/blob/main/py-scripts/export-ggb-clean-asy.py */ /* A few re-additions are done using bubu-asy.py. This adds the dps, xmin, linewidth, fontsize and directions. https://github.com/Bubu-Droid/dotfiles/blob/master/bubu-scripts/bubu-asy.py */ pair A = (24.81281,-5.45037); pair B = (-6.39088,-5.19529); pair C = (0.26530,21.43292); pair P = (18.77311,1.16403); pair Q = (18.92617,19.88811); pair O = (9.29559,5.02962); pair D = (27.95646,3.48480); pair F = (26.85608,19.23164); pair S = (18.71945,-5.40056); pair E = (26.32491,12.81529); pair X = (25.56886,3.68246); pair Y = (23.63508,11.33449); import graph; size(10cm); pen dps = linewidth(0.5) + fontsize(13); defaultpen(dps); real xmin = -5, xmax = 5, ymin = -5, ymax = 5; pen ffxfqq = rgb(1.,0.49803,0.); draw((24.64484,9.50029)--(26.47904,10.51004)--(25.46928,12.34425)--Y--cycle, linewidth(0.6) + blue); draw((27.65551,3.50972)--(27.82825,5.59636)--(25.74160,5.76910)--X--cycle, linewidth(0.6) + blue); draw((15.86788,11.32006)--(17.00668,13.07706)--(15.24968,14.21586)--(14.11088,12.45886)--cycle, linewidth(0.6) + blue); draw(A--B, linewidth(0.6)); draw(B--C, linewidth(0.6)); draw(C--A, linewidth(0.6)); draw(circle(O, 18.72470), linewidth(0.6)); draw(C--O, linewidth(0.6)); draw(O--D, linewidth(0.6) + ffxfqq); draw((20.10150,4.13506)--(19.29048,3.31085), linewidth(0.6) + ffxfqq); draw((20.10150,4.13506)--(19.43705,5.08142), linewidth(0.6) + ffxfqq); draw((18.62602,4.25721)--(17.81500,3.43300), linewidth(0.6) + ffxfqq); draw((18.62602,4.25721)--(17.96157,5.20357), linewidth(0.6) + ffxfqq); draw(D--Q, linewidth(0.6)); draw(A--F, linewidth(0.6)); draw(Q--S, linewidth(0.6)); draw(Q--F, linewidth(0.6) + ffxfqq); draw(B--E, linewidth(0.6)); draw(circle((27.14069,8.15005), 4.73602), linewidth(0.6) + linetype("4 4") + red); draw(C--Q, linewidth(0.6) + ffxfqq); draw((11.07121,20.53837)--(10.26018,19.71415), linewidth(0.6) + ffxfqq); draw((11.07121,20.53837)--(10.40676,21.48473), linewidth(0.6) + ffxfqq); draw((9.59573,20.66051)--(8.78471,19.83630), linewidth(0.6) + ffxfqq); draw((9.59573,20.66051)--(8.93128,21.60687), linewidth(0.6) + ffxfqq); draw(C--D, linewidth(0.6)); draw(O--Q, linewidth(0.6)); dot("$A$", A, SE); dot("$B$", B, SW); dot("$C$", C, NW); dot("$P$", P, W); dot("$Q$", Q, NW); dot("$O$", O, W); dot("$D$", D, SE); dot("$F$", F, NE); dot("$S$", S, dir(270)); dot("$E$", E, NE); dot("$X$", X, SW); dot("$Y$", Y, NW); [/asy]$

Claim: $\triangle QCP \cong \triangle OCB$ .
Proof. Note that $QP=r=OB$ and $PC=BC$ and $\angle QPC = \angle SPA=90^{\circ}-\angle A=\angle OBC$ . $\blacksquare$
This gives us that $QC=CO=CD$ .

Claim: $Q$ is the reflection of $O$ over $CD$ .
Proof. Note that we already have $CQ=CO$ . Now note that, $\angle OCQ=\angle OCA+\angle PCQ=90^{\circ}-\angle B+\angle BCO = 90^{\circ}-\angle B+90^{\circ}-\angle A=C .$ Now, $\angle OCD=\angle OCA+\angle ACD=90^{\circ}-\angle B + \angle ABD = 90^{\circ}-\angle B+(\angle B-\angle PBC) =90^{\circ}-\angle PBC=90^{\circ}- (90^{\circ}-\frac{\angle C}{2}) =\frac{\angle C}{2} .$ Now since $CO = CQ$ , this gives us that $Q$ is indeed the reflection $O$ over $CD$ . $\blacksquare$
Note that from this claim, we get $QD=OD$ . It also gives us that $OQ\perp CD$ . Combining all these information together, we get that $QCOD$ is a rhombus. This gives us that $CQ\parallel OD$ which further gives $OD\perp AE$ .
Let $X=AE\cap OD$ and $Y=BE\cap DQ$ .
Note that we get, $\angle DXE=\angle DYE=90^{\circ}\implies DXYE$ is cyclic.
Now to finish, we have, $\measuredangle BEA=\measuredangle YEX=\measuredangle YDX =\measuredangle QDO=\measuredangle OCQ=\measuredangle C =\measuredangle BCA$ which gives us that $E$ indeed lies on $\odot(ABC)$ and we are done.

This post has been edited 2 times. Last edited by kamatadu, Sep 26, 2024, 8:18 PM

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

60 posts

#28 h Oct 7, 2024, 2:24 PM • 1 Y

Y by alexanderhamilton124

The problem is asking to prove that $QC=QD=QP$ . Let $O$ be the circumcenter of $ABC$ . Note that, $QPC$ is congruent to $OBC$ , which implies $QP=QC=r$ . Now let $AE$ intersects $CQ$ at $X$ . Note that, $AXQS$ is cyclic. Now from this, and the cyclic quad $ABCD$ we can show, $\angle DPC =\frac{1}{2}\angle PQC$ proving our claim.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

1363 posts

#29 h Nov 1, 2024, 2:38 AM

Y by

Note that the circumradius of $\triangle CPD$ is $r$ as: $\tfrac{CP}{2 \sin(\angle BDC)} = r.$ Also notice that: $\angle CPQ = \angle APS = 90^\circ - A =90^\circ - \angle PDC$ which implies $Q$ is the circumcenter of $\triangle PDC$ . Notice that: $\angle BPC = 90^\circ - \tfrac{C}{2} \implies \angle DQC = 2 \angle BPC = 180^\circ - C \implies \angle AEB = \angle ACB$ and we are done.

This post has been edited 1 time. Last edited by Saucepan_man02, Nov 1, 2024, 2:38 AM
Reason: Brackets

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

8874 posts

#30 h Dec 13, 2024, 4:19 AM

Y by

This is (thankfully) a lot easier than G1 ... the conditions of the problem basically solve themselves.

Claim: [Main Claim] $Q$ is the circumcenter of triangle $PCD$ .

Proof: Note that by the Law of Sines, $2R_{PCD} = \frac{CD}{\sin \angle CPD} = \frac{CD}{\sin \angle BCD} = 2R_{ABC}$ . Hence it suffices to show that the circumcenter $Q'$ of triangle $CPD$ lies on $\overline{PS}$ . But this is clear because
$\angle CPQ' = 90^\circ - \angle CPD = 90^\circ - \angle A = \angle CPQ. \ \blacksquare$ So $\angle BEA = 180^\circ - \angle CQD = 180^\circ - 2\angle CPB = \angle BCA$ which finishes.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

167 posts

#31 h Dec 27, 2024, 11:54 AM

Y by

Easier then G1
Also the condition seemed weird but it’s not too difficult to cope with

avisioner wrote:

Let $ABC$ be a triangle with $AC > BC,$ let $\omega$ be the circumcircle of $\triangle ABC,$ and let $r$ be its radius. Point $P$ is chosen on $\overline{AC}$ such taht $BC=CP,$ and point $S$ is the foot of the perpendicular from $P$ to $\overline{AB}$ . Ray $BP$ mets $\omega$ again at $D$ . Point $Q$ is chosen on line $SP$ such that $PQ = r$ and $S,P,Q$ lie on a line in that order. Finally, let $E$ be a point satisfying $\overline{AE} \perp \overline{CQ}$ and $\overline{BE} \perp \overline{DQ}$ . Prove that $E$ lies on $\omega$ .

First, by angle chasing it’s easy to see that $DP=DB$ so the condition of $C,D$ are in fact symmetrical wrt $A,B$
Also notice that $\measuredangle AEB=\measuredangle CQD$ so we only need to prove that $\measuredangle ACB=\measuredangle CQD$
(We can remove $E$ from our figure now)

Now let $\measuredangle CBA=\beta$ and $\measuredangle DAB=\delta$
Applying law of sin on $\triangle CAP$ we know $CA=CP=2r\sin\beta$
Since $\measuredangle CPQ=\measuredangle BPS=90^{\circ}-\beta$ , applying law of cos on $\triangle CPQ$ we know $CQ=r$
(Notice that $\cos(90^{\circ}-\theta=\sin\theta$ )

Then $\measuredangle PAC=\measuredangle CPA=\beta+\delta\implies \measuredangle BCA=180^{\circ}-2\beta-2\delta$
So $\measuredangle ACB=2\beta+2\delta=\measuredangle CQD$ , Done

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

237 posts

deduck

#32 h Dec 28, 2024, 2:57 AM • 1 Y

Y by blueberryfaygo_55

hi guys idk if i did directed angle for this right pls check if my directed angles are right........

HELP

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

388 posts

#33 h Dec 28, 2024, 3:02 AM

Y by

deduck wrote:

hi guys idk if i did directed angle for this right pls check if my directed angles are right........

HELP

You can't halve a directed angle.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

237 posts

deduck

#34 h Dec 28, 2024, 3:04 AM

Y by

im dumb $\text{[math]}$

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

237 posts

deduck

#35 h Dec 28, 2024, 3:08 AM

Y by

Ok its not that deep there isnt even config issues
ok

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

maths_enthusiast_0001

133 posts

maths_enthusiast_0001

#36 h Jan 13, 2025, 6:27 PM • 1 Y

Y by L13832

Nice question :coolspeak:

:coolspeak:

Solution

Attachments:

This post has been edited 1 time. Last edited by maths_enthusiast_0001, Mar 27, 2025, 6:59 AM
Reason: diagram attachment

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

38 posts

Bonime

#37 h Jan 14, 2025, 12:52 PM

Y by

A different solution with Power of Point and some laws of cossines and sines:

Let $O$ be the circumcenter of $\omega$ and $\Gamma$ be the circle with center $Q$ and radius $r$ .
$\boxed{\text{Lemma:}}$ $Q$ is the center of $(CPD)$
Prove: We´ll take two power of points: one from $A$ in $\Gamma$ and other in $B$ in $\Gamma$ too $C \in \Gamma$ $\iff \text{Pot}_\Gamma A = AQ^2 - r^2=AP\cdot AC=AP^2+AP\cdot PC$ $\iff AQ^2 -QP^2 -PA^2=AP\cdot PC$ But, notice that $\angle APS = 90 -\angle A \Rightarrow \angle APQ=90 +\angle A$ , so $AQ^2 -QP^2 -PA^2=-2PA\cdot QP\cdot \text{cos}(90+\angle A)=2rAP\cdot \text{sin} \angle A (\text{Law of cossines at the triangle APQ})$ $=AP\cdot BC=AP\cdot PC \text{(Law of sines at the triangle ABC)}$ $\Rightarrow C \in \Gamma$ Equivalently $D \in \Gamma$ $\iff \text{Pot}_\Gamma B=BQ^2 -QP^2=BP\cdot BD=BP^2 +BP\cdot PD$ $\iff BQ^2 -QP^2 -PB^2=BP\cdot PD$ But, note that $\angle BPS=90 \angle SBP \Rightarrow \angle BPQ =90+ \angle SBP$ , therefore $BQ^2 -QP^2 -PB^2=-2QP\cdot PB\cdot \text{cos}(90+\angle SBP)=2rPB\cdot \text{sin}\angle SBP \text{(Law of cossines at the triangle BPQ)}$ $PB\cdot AD=PB\cdot PD \text{(Law of sines at the triangle ACD)}$ $\Rightarrow D \in \Gamma \blacksquare$ Finally, we note that $CQDO$ is paralelogram $\Rightarrow AC//DQ \Rightarrow BE \bot AC$ and then $\angle QPD=\angle QDP \Rightarrow \angle EBP=\angle PBA \Rightarrow \angle SPA=\angle SPC= 90 - \angle EBC \Rightarrow \angle A= \angle EBC \Rightarrow ABC=90 \Rightarrow E \in \omega$ $\blacksquare$

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

5419 posts

#38 h Jan 22, 2025, 9:51 PM • 4 Y

Y by OronSH, centslordm, ihatemath123, imagien_bad

You have got to be kidding me.

https://cdn.artofproblemsolving.com/attachments/6/3/ae3a9f4d9998b0410489fbfb96db7c40f484b9.png

Reference $\triangle MCD$ for $M$ the midpoint of minor arc $AB$ . We have $MC\perp BP$ since $CB=CP$ and $MC$ bisects $\angle BCP$ ; combining with the analogous $MD\perp AP$ reveals that $P$ is the orthocentre of $\triangle MCD$ , with $A$ and $B$ its reflections across $MD$ and $MC$ . Now, as $MO=r$ and $MO\perp AB$ , equivalently $Q$ is such that $MOQP$ is a parallelogram, i.e., $\vec{Q}=\vec{C}+\vec{D}$ . But $E$ the reflection of $P$ over $CD$ works. $\blacksquare$

Lessons Learned. Don't postban me

This post has been edited 2 times. Last edited by peace09, Jan 22, 2025, 11:19 PM

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

20 posts

#39 h Feb 4, 2025, 12:43 PM

Y by

Let, line AE intersect CQ at F and
$\angle BAC = x$ and $\angle CAE = y$
$\angle ASP = 90$
$\angle SPA = 90 - x =\angle CPQ$
On the other hand, $\angle ASQ = \angle AEQ = 90$ and thus quadrilateral $ASFQ$ is cyclic.So $\angle SAE = x + y = \angle SQC$
$\angle PCQ = 90 - y$
By sin law in triangle $ABC$ ,
$\frac{BC}{\sin \angle BAC}=2r$ (where r is the circumradius of the triangle.)

$\frac{BC}{r}=2\sin \angle BAC = 2\sin x$

By sin law in triangle $PQC$ ,

$\frac{PQ}{\sin \angle PCQ}=\frac{PC}{\sin \angle QPC}$

$\frac{r}{\sin 90 - y}=\frac{BC}{\sin x+y}$

$\frac{BC}{r}=\frac{\sin x+y}{\sin 90 - y}=2\sin x$

$\sin x + y = 2\sin x \sin 90-y = 2 \sin x \cos y$

$\sin (x+y) + \sin(x-y)=\sin (x+y)$

$\sin (x-y) = 0$

So either $x=y$ or $y=180-x$ .The 2nd option doesnt make any sense.

So $x=y$ , $\angle BAP = \angle EAP$

AP bisects $\angle BAE$ .

Let $\angle BPC=z=\angle PBC$
$\angle BCA = \angle BCP = 180 - z$
D is on $\omega$ so quadrilateral $ABCD$ is cyclic.
Thus.
$\angle BCP = 180 - 2z=\angle ADP$
$\angle BPC = z = \angle APD = \angle DAP$
$\angle AED = z - x = \angle ABP$
$\angle DPQ = 90 - x - z$
Let $\angle PDQ = w$
$\angle PQD = 90 - x + z - w$
We know that AD=DP from the above angle chasing.
By sin law on triangle $ADB$

$\frac{AD}{\sin \angle ABD}=2r$

$\frac{DP}{r}=2\sin z - x$

By sin law on triangle $DPQ$ ,

$\frac{DP}{\sin \angle DQP}=\frac{PQ}{\sin \angle PDQ}$

$\frac{DP}{r}=\frac{\sin 90 - x + z - w}{\sin w}=2sin z - x$

$\cos x - z + w = 2\sin z-x \sin w$

$\cos (x - z + w) = \cos (z-x-w) - \cos (z-x+w)$

$\cos z - x + w = 0$

So either $w=90+x-z$ or $w=x-z$
Let the lines DQ and BE intersect at G.
$\angle DGB = 90$
If $w=x-z$ ,then, $\angle DBG = 90 -x+z=\angle DBE$
$\angle ABE = 90$ which is impossible as triangle $ABC$ is acute.
Thus
$w=90+x-z$
$\angle DBG = z-x = \angle DBE$

Thus P is the incenter of triangle $AEB$ .

Now $\angle DBE = z-x = \angle EAD$

But these are the angles subtended on the same arc.
Thus quadrilateral $ADEB$ is cyclic.
Therefore E lies on $\omega$ .

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

676 posts

#40 h Mar 10, 2025, 7:55 PM

Y by

Claim: $Q$ is circumcenter of $DPC,$ and the cirumcradius is $r.$
Proof: Note that $2r = \frac{DC}{\sin{\angle DBC}} = \frac{DC}{\sin{\angle DPC}}$ so the circumradii are the same. Furthermore, note that $\angle QPC = \angle APS = 90 - \angle A.$ Applying this with $PQ = r$ condition, we get our desired claim.

Let $X$ lie on $(ABC)$ so that $D$ is the arc midpoint of $AE$ in $(ABC).$ We prove $X$ satisfies $E$ 's conditions.
Claim: $C$ is the arc midpoint of $XB$
Proof: $\angle XBC = \angle DBC - \angle DBX = \angle BPC - \angle ABD = \angle BAC.$

Now, we can finish. Observe that $\angle XAC = \angle BAC = 90 - (90 - \angle BAC) = 90 - \angle QPC = 90 - \angle QCP$ so $\angle(AE, QC) - 90.$ Furthermore, $\angle QDB = \angle DPQ = \angle SPB = 90 - \angle SBP = 90 - \angle DBE$ so $\angle (BE, DQ) = 90.$

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

4239 posts

#41 h Apr 17, 2025, 6:10 PM

Y by

What a funny length condition ...

Let $O$ be the center of $\omega$ . Note that $BO = PQ$ and that $CB = CP$ , and $\angle CPQ = 90 - \angle A = \angle CBO$ , so triangles $CBO$ and $CPQ$ are congruent.

Then $\angle QCO = \angle C$ and $\angle COD = 2 \angle CBD = 180 - \angle C$ , so lines $OD$ and $CQ$ are parallel. Thus from $CQ = CO = OD$ it follows that $OCQD$ is a rhombus.

Thus the point $E$ satisfies $AE \perp OD$ and $BE \perp CO$ . Let $E'$ be the reflection of $P$ over $CD$ . We claim that $E' = E$ .

We have $\angle BDE' = 2 \angle BDC = \angle BOC$ , from which it follows indeed that $E'$ is the reflection of $B$ over $CO$ . Note also that the problem is symmetric now; indeed, $\angle CPB = \angle CBP = \angle CAD = \angle APD$ so $DP = DA$ , so $E'$ is also the reflection of $A$ over $DO$ . We are done.

Z K Y

The post below has been deleted. Click to close.

This post has been deleted. Click here to see post.

1311 posts

ezpotd

#42 h May 25, 2025, 7:48 PM

Y by

Claim: $Q$ is the circumcenter of $CPD$ .
Proof: Note that by SAS congruency, $CQP$ is congruent to $BOC$ , so $CQ = PQ$ . Next, $DP = \frac{PC \cdot AP}{BP} = \frac{AC- BC}{2 \sin \frac C2}= \frac{2R \sin (\frac{A + B}{2} - \frac{A - B}{2}) - 2R \sin (\frac{A+B}{2} + \frac{A-B}{2} )}{2 \sin \frac C2} = 2R \sin \frac{A -B}{2}$ , so letting $C'$ be the point such that $CC'AB$ is an isosceles trapezoid, we have $CC'O$ is congruent to $PDQ$ by SAS, so $DQ = PQ$ .

Now we have $\angle CQP = 180 - \angle C$ , angle chasing to find $\angle AEB = \angle C$ finishes.

This post has been edited 1 time. Last edited by ezpotd, May 28, 2025, 1:24 AM

Z K Y

N Quick Reply

G

H

=

© 2025 AoPS Incorporated

a