1991 AIME Problems/Problem 4
Contents
[hide]Problem
How many real numbers ![]() satisfy the equation
satisfy the equation ![]() ?
?
Solution
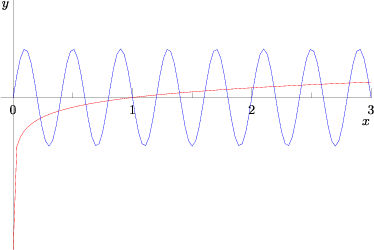
The range of the sine function is ![]() . It is periodic (in this problem) with a period of
. It is periodic (in this problem) with a period of ![]() .
.
Thus, ![]() , and
, and ![]() . The solutions for
. The solutions for ![]() occur in the domain of
occur in the domain of ![]() . When
. When ![]() the logarithm function returns a positive value; up to
the logarithm function returns a positive value; up to ![]() it will pass through the sine curve. There are exactly 10 intersections of five periods (every two integral values of
it will pass through the sine curve. There are exactly 10 intersections of five periods (every two integral values of ![]() ) of the sine curve and another curve that is
) of the sine curve and another curve that is ![]() , so there are
, so there are ![]() values (the subtraction of 6 since all the “intersections” when
values (the subtraction of 6 since all the “intersections” when ![]() must be disregarded). When
must be disregarded). When ![]() , there is exactly
, there is exactly ![]() touching point between the two functions:
touching point between the two functions: ![]() . When
. When ![]() or
or ![]() , we can count
, we can count ![]() more solutions. The solution is
more solutions. The solution is ![]() .
.
Solution 2
Notice that the equation is satisfied twice for every sine period (which is ![]() ), except in the sole case when the two equations equate to
), except in the sole case when the two equations equate to ![]() . In that case, the equation is satisfied twice but only at the one instance when
. In that case, the equation is satisfied twice but only at the one instance when ![]() . Hence, it is double-counted in our final solution, so we have to subtract it out. We then compute:
. Hence, it is double-counted in our final solution, so we have to subtract it out. We then compute:
![]()
See also
| 1991 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









