1995 AIME Problems/Problem 1
Problem
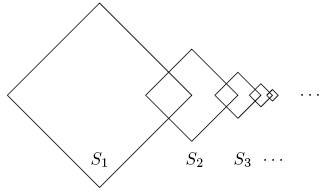
Square ![]() is
is ![]() For
For ![]() the lengths of the sides of square
the lengths of the sides of square ![]() are half the lengths of the sides of square
are half the lengths of the sides of square ![]() two adjacent sides of square
two adjacent sides of square ![]() are perpendicular bisectors of two adjacent sides of square
are perpendicular bisectors of two adjacent sides of square ![]() and the other two sides of square
and the other two sides of square ![]() are the perpendicular bisectors of two adjacent sides of square
are the perpendicular bisectors of two adjacent sides of square ![]() The total area enclosed by at least one of
The total area enclosed by at least one of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Solution
The sum of the areas of the squares if they were not interconnected is a geometric sequence:
Then subtract the areas of the intersections, which is ![]() :
:
The majority of the terms cancel, leaving ![]() , which simplifies down to
, which simplifies down to ![]() . Thus,
. Thus, ![]() .
.
Alternatively, take the area of the first square and add ![]() of the areas of the remaining squares. This results in
of the areas of the remaining squares. This results in ![$1+ \frac{3}{4}\left[\left(\frac{1}{2}\right)^2 + \ldots + \left(\frac{1}{16}^2\right)\right]$](http://latex.artofproblemsolving.com/f/1/a/f1ad25f7cc94b2582dca91b9ebdd23b3bec63068.png) , which when simplified will produce the same answer.
, which when simplified will produce the same answer.
See also
| 1995 AIME (Problems • Answer Key • Resources) | ||
| Preceded by First Question |
Followed by Problem 2 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()





![$1^2 + \left(\frac{1}{2}\right)^2 + \left(\frac{1}{4}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{16}\right)^2 - \left[\left(\frac{1}{4}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{16}\right)^2 + \left(\frac{1}{32}\right)^2\right]$](http://latex.artofproblemsolving.com/6/0/9/609fafb8171705bc071b28b2302550e4282c0eab.png)




