2007 Cyprus MO/Lyceum/Problem 23
Problem
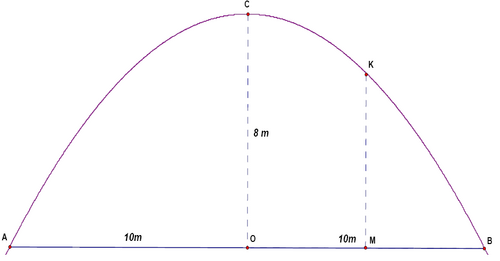
In the figure above the right section of a parabolic tunnel is presented. Its maximum height is ![]() and its maximum width is
and its maximum width is ![]() . If M is the midpoint of
. If M is the midpoint of ![]() , then the height
, then the height ![]() of the tunnel at the point
of the tunnel at the point ![]() is
is
![]()
Solution
Since it is a parabolic tunnel, the equation of the tunnel is a quadratic. We have three points: (0,8), (10,0), and (-10,0). Since we have both of the roots, we multiply ![]() . But we also have
. But we also have ![]() , so
, so ![]() . Thus the equation of the parabola is
. Thus the equation of the parabola is ![]() . Now the height of the tunnel at M is the value of the y coordinate when
. Now the height of the tunnel at M is the value of the y coordinate when ![]() , or
, or ![]() .
. ![]()
See also
| 2007 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||