2007 Cyprus MO/Lyceum/Problem 30
Problem
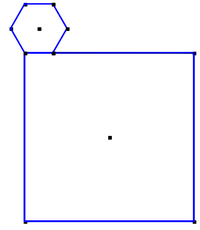
A coin with a shape of a regular hexagon of side 1 is tangent to a square of side 6, as shown in the figure. The coin rotates on the perimeter of the square, until it reaches its original position. The length of the line which is being inscribed by the centre of the hexagon is
![]()
Solution
Each time the hexagon moves, its center travels ![]() of a circle with radius
of a circle with radius ![]() .
.
Each time the hexagon goes around a corner, it's center travels ![]() , or
, or ![]() of a circle.
of a circle.
The hexagon moves ![]() times (
times (![]() times per side), and goes around
times per side), and goes around ![]() corners.
corners.
![]()
![]()
See also
| 2007 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 29 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||