2019 AMC 10B Problems/Problem 23
- The following problem is from both the 2019 AMC 10B #23 and 2019 AMC 12B #20, so both problems redirect to this page.
Contents
[hide]Problem
Points ![]() and
and ![]() lie on circle
lie on circle ![]() in the plane. Suppose that the tangent lines to
in the plane. Suppose that the tangent lines to ![]() at
at ![]() and
and ![]() intersect at a point on the
intersect at a point on the ![]() -axis. What is the area of
-axis. What is the area of ![]() ?
?
![]()
Solution 1
First, observe that the two tangent lines are of identical length. Therefore, supposing that the point of intersection is ![]() , the Pythagorean Theorem gives
, the Pythagorean Theorem gives ![]() . This simplifies to
. This simplifies to ![]() .
.
Further, notice (due to the right angles formed by a radius and its tangent line) that the quadrilateral (a kite) ![]() is cyclic.
is cyclic.
Therefore, we can apply Ptolemy's Theorem to give:
![]() , where
, where ![]() is the radius of the circle and
is the radius of the circle and ![]() is the distance between the circle's center and
is the distance between the circle's center and ![]() . Therefore,
. Therefore, ![]() .
.
Using the Pythagorean Theorem on the right triangle ![]() (or
(or ![]() ), we find that
), we find that ![]() , so
, so ![]() , and thus the area of the circle is
, and thus the area of the circle is ![]() .
.
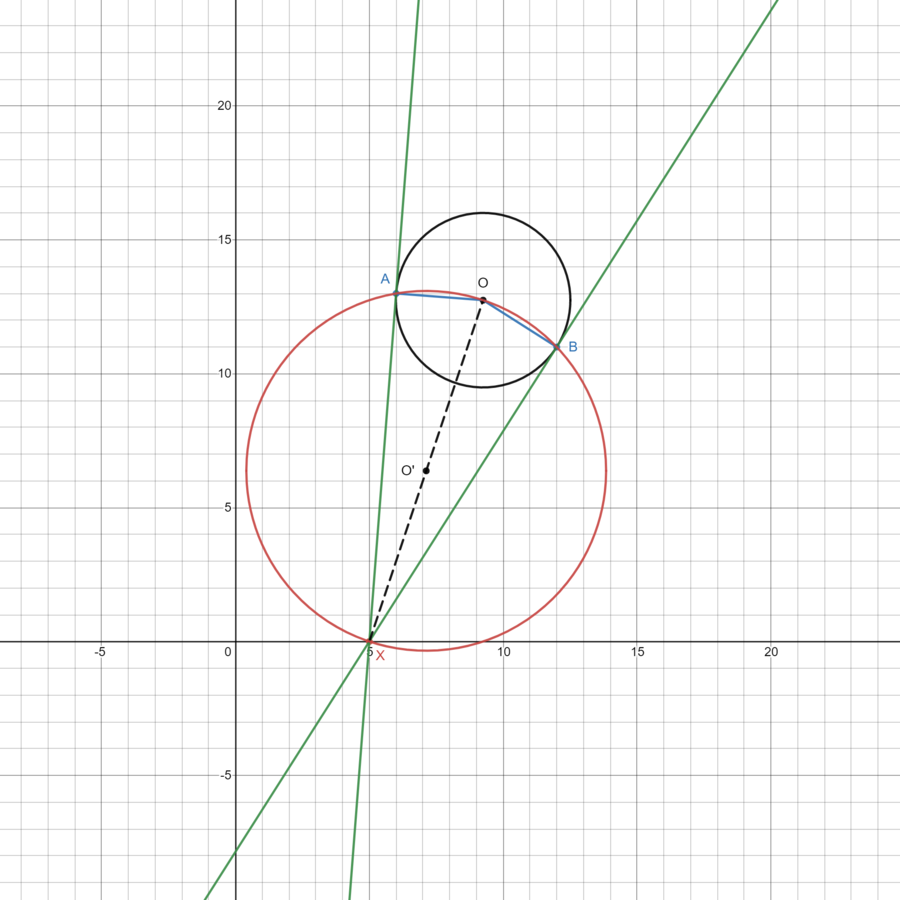
Diagram for Solution 1
~BakedPotato66
Solution 2 (coordinate bash)
We firstly obtain ![]() as in Solution 1. Label the point
as in Solution 1. Label the point ![]() as
as ![]() . The midpoint
. The midpoint ![]() of segment
of segment ![]() is
is ![]() . Notice that the center of the circle must lie on the line passing through the points
. Notice that the center of the circle must lie on the line passing through the points ![]() and
and ![]() . Thus, the center of the circle lies on the line
. Thus, the center of the circle lies on the line ![]() .
.
Line ![]() is
is ![]() . Therefore, the slope of the line perpendicular to
. Therefore, the slope of the line perpendicular to ![]() is
is ![]() , so its equation is
, so its equation is ![]() .
.
But notice that this line must pass through ![]() and
and ![]() . Hence
. Hence ![]() . So the center of the circle is
. So the center of the circle is ![]() .
.
Finally, the distance between the center, ![]() , and point
, and point ![]() is
is ![]() . Thus the area of the circle is
. Thus the area of the circle is ![]() .
.
Solution 3
The midpoint of ![]() is
is ![]() . Let the tangent lines at
. Let the tangent lines at ![]() and
and ![]() intersect at
intersect at ![]() on the
on the ![]() -axis. Then
-axis. Then ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() . Let the center of the circle be
. Let the center of the circle be ![]() . Then
. Then ![]() is similar to
is similar to ![]() , so
, so ![]() .
The slope of
.
The slope of ![]() is
is ![]() , so the slope of
, so the slope of ![]() is
is ![]() . Hence, the equation of
. Hence, the equation of ![]() is
is ![]() . Letting
. Letting ![]() , we have
, we have ![]() , so
, so ![]() .
.
Now, we compute ![]() ,
,
![]() , and
, and
![]() .
.
Therefore ![]() ,
and consequently, the area of the circle is
,
and consequently, the area of the circle is ![]() .
.
Solution 4 (how fast can you multiply two-digit numbers?)
Let ![]() be the intersection on the x-axis. By Power of a Point Theorem,
be the intersection on the x-axis. By Power of a Point Theorem, ![]() . Then the equations for the tangent lines passing
. Then the equations for the tangent lines passing ![]() and
and ![]() , respectively, are
, respectively, are ![]() and
and ![]() . Then the lines normal (perpendicular) to them are
. Then the lines normal (perpendicular) to them are ![]() and
and ![]() . Solving for
. Solving for ![]() , we have
, we have
![]()
![]()
![]()
After condensing, ![]() . Then, the center of
. Then, the center of ![]() is
is ![]() . Apply distance formula. WLOG, assume you use
. Apply distance formula. WLOG, assume you use ![]() . Then, the area of
. Then, the area of ![]() is
is ![\[\left(\sqrt{\frac{1^2}{4^2}+\frac{13^2}{4^2}}\right)^2\pi=\frac{170\pi}{16} \implies \boxed{\textbf{(C) }\frac{85}{8}\pi}.\]](http://latex.artofproblemsolving.com/4/c/4/4c42ef66d5323c30e0d632da741e58d3926ad4d5.png)
Solution 5 (tangent cheese)
After getting ![]() , let
, let ![]() . Get the slopes of the lines
. Get the slopes of the lines ![]() and
and ![]() , namely
, namely ![]() ,
, ![]() . Then, use tangent angle subtraction to get
. Then, use tangent angle subtraction to get ![]() . Then, apply tangent double angle to get
. Then, apply tangent double angle to get ![]() . Solving, we obtain
. Solving, we obtain ![]() . Then, note that
. Then, note that ![]() , so
, so ![]() . Finishing off, we obtain
. Finishing off, we obtain ![]() .
.
~SigmaPiE
Video Solution
For those who want a video solution: (Is similar to Solution 1) https://youtu.be/WI2NVuIp1Ik
Video Solution by TheBeautyofMath
~IceMatrix
Video Solution by The Power of Logic
https://www.youtube.com/watch?v=sQIWSrio_Hc
~The Power of Logic
See Also
| 2019 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2019 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 19 |
Followed by Problem 21 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()