Difference between revisions of "2010 AMC 12A Problems/Problem 8"
Sakshamsethi (talk | contribs) (→Solution) |
Sugar rush (talk | contribs) |
||
| Line 25: | Line 25: | ||
-vsamc | -vsamc | ||
| − | ==Video Solution== | + | ==Video Solution by the Beauty of Math== |
https://youtu.be/kU70k1-ONgM?t=785 | https://youtu.be/kU70k1-ONgM?t=785 | ||
| − | |||
| − | |||
== See also == | == See also == | ||
Revision as of 20:19, 6 December 2020
Contents
[hide]Problem
Triangle ![]() has
has ![]() . Let
. Let ![]() and
and ![]() be on
be on ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() . Let
. Let ![]() be the intersection of segments
be the intersection of segments ![]() and
and ![]() , and suppose that
, and suppose that ![]() is equilateral. What is
is equilateral. What is ![]() ?
?
![]()
Solution
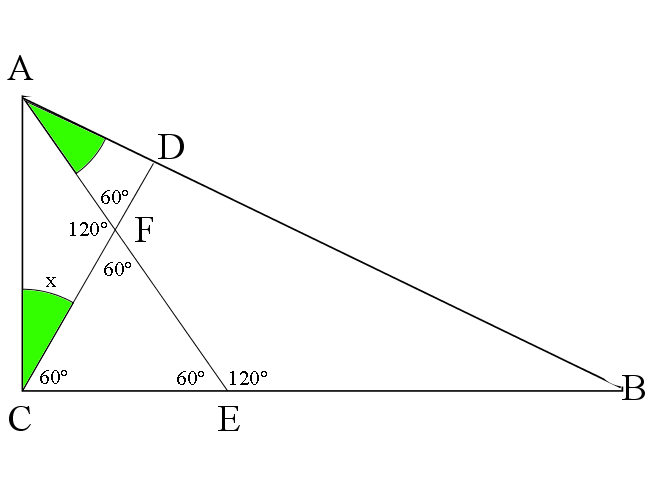
Let ![]() .
.

Since ![]() and the angle between the hypotenuse and the shorter side is
and the angle between the hypotenuse and the shorter side is ![]() , triangle
, triangle ![]() is a
is a ![]() triangle, so
triangle, so ![]() .
.
Solution 2(Trig and Angle Chasing)
Let ![]() . Let
. Let ![]() . Because
. Because ![]() is equilateral, we get
is equilateral, we get ![]() , so
, so ![]() . Because
. Because ![]() is equilateral, we get
is equilateral, we get ![]() . Angles
. Angles ![]() and
and ![]() are vertical, so
are vertical, so ![]() . By triangle
. By triangle ![]() , we have
, we have ![]() , and because of line
, and because of line ![]() , we have
, we have ![]() . Because Of line
. Because Of line ![]() , we have
, we have ![]() , and by line
, and by line ![]() , we have
, we have ![]() . By quadrilateral
. By quadrilateral ![]() , we have
, we have ![]() .
.
By the Law of Sines, we have ![]() . By the sine addition formula(which states
. By the sine addition formula(which states ![]() by the way), we have
by the way), we have ![]() . Because cosine is an even function, and sine is an odd function, we have
. Because cosine is an even function, and sine is an odd function, we have ![]() . We know that
. We know that ![]() , and
, and ![]() , hence
, hence ![]() . The only value of
. The only value of ![]() that satisfies
that satisfies ![]() (because
(because ![]() is an angle of the triangle) is
is an angle of the triangle) is ![]() . We seek to find
. We seek to find ![]() , which as we found before is
, which as we found before is ![]() , which is
, which is ![]() . The answer is
. The answer is ![]()
-vsamc
Video Solution by the Beauty of Math
https://youtu.be/kU70k1-ONgM?t=785
See also
| 2010 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 7 |
Followed by Problem 9 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









