Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2018 AMC 10B Problems/Problem 24"

m (→‎Solution 2 (Area Subtraction))
m (→‎Solution 3: Minor cosmetic changes.)
Line 98: Line 98:
 
~BJHHar
 
~BJHHar
  
−
==Solution 3 ==
+
==Solution 3 (Area Subtraction)==
 
<asy>
 
<asy>
−
pair A,B,C,D,E,F,W,X,Y,Z,M,N,O,P,Q,R;
+
/* Made by MRENTHUSIASM */
−
A=(0,sqrt(3));
+
size(200);
−
B=(1,sqrt(3));
+
draw(polygon(6));
−
C=(3/2,sqrt(3)/2);
+
pair A, B, C, D, E, F, X, Y, Z, M, N, O, P, Q, R;
−
D=(1,0);
+
A = dir(120);
−
E=(0,0);
+
B = dir(60);
−
F=(-1/2,sqrt(3)/2);
+
C = dir(0);
−
X=(1/2, sqrt(3));
+
D = dir(300);
−
Y=(5/4, sqrt(3)/4);
+
E = dir(240);
−
Z=(-1/4, sqrt(3)/4);  
+
F = dir(180);
−
M=(0,sqrt(3)/2);
+
X = midpoint(A--B);
−
N=(3/4,3sqrt(3)/4);
+
Y = midpoint(C--D);
−
O=(3/4,sqrt(3)/4);
+
Z = midpoint(E--F);
−
P=(3/8,7sqrt(3)/8);
+
M = intersectionpoint(A--E,X--Z);
−
Q=(9/8, 3sqrt(3)/8);
+
N = intersectionpoint(A--C,X--Y);
−
R=(0,sqrt(3)/4);
+
O = intersectionpoint(C--E,Y--Z);
−
label("$A$",A,NW);
+
P = intersectionpoint(A--C,X--Z);
−
label("$B$",B,NE);
+
Q = intersectionpoint(C--E,X--Y);
−
label("$C$",C,ESE);
+
R = intersectionpoint(A--E,Y--Z);
−
label("$D$",D,SE);
+
fill(M--P--N--Q--O--R--cycle,mediumgray);
−
label("$E$",E,SW);
+
dot("$A$",A,1.5*dir(A),linewidth(4));
−
label("$F$",F,WSW);
+
dot("$B$",B,1.5*dir(B),linewidth(4));
−
label("$X$", X, N);
+
dot("$C$",C,1.5*dir(C),linewidth(4));
−
label("$Y$", Y, ESE);
+
dot("$D$",D,1.5*dir(D),linewidth(4));
−
label("$Z$", Z, WSW);
+
dot("$E$",E,1.5*dir(E),linewidth(4));
−
label("$M$", M, NW);
+
dot("$F$",F,1.5*dir(F),linewidth(4));
−
label("$N$", N, NE);
+
dot("$X$",X,1.5*dir(X),linewidth(4));
−
label("$O$", O, SE);
+
dot("$Y$",Y,1.5*dir(Y),linewidth(4));
−
label("$P$", P, NNW);
+
dot("$Z$",Z,1.5*dir(Z),linewidth(4));
−
label("$Q$", Q, ESE);
+
dot("$M$",M,1.5*dir(165),linewidth(4));
−
label("$R$", R, SW);
+
dot("$N$",N,1.5*dir(45),linewidth(4));
−
fill((0,sqrt(3)/2)--(3/8,7sqrt(3)/8)--(3/4,3sqrt(3)/4)--(9/8, 3sqrt(3)/8)--(3/4,sqrt(3)/4)--(0,sqrt(3)/4)--cycle,gray);
+
dot("$O$",O,1.5*dir(-75),linewidth(4));
−
draw(A--B--C--D--E--F--cycle);
+
dot("$P$",P,1.5*dir(105),linewidth(4));
−
draw(A--C--E--cycle);
+
dot("$Q$",Q,1.5*dir(-15),linewidth(4));
−
draw(X--Y--Z--cycle);
+
dot("$R$",R,1.5*dir(-135),linewidth(4));
−
draw(M--N--O--cycle);
+
draw(A--C--E--cycle^^X--Y--Z--cycle);
 +
draw(M--N--O--cycle,dashed);
 
</asy>
 
</asy>
  
−
Now, if we look at the figure, we can see that the complement of the hexagon we are trying to find is composed of <math>3</math> isosceles trapezoids (<math>AXFZ</math>, <math>XBCY</math>, and <math>ZYED</math>), and <math>3</math> right triangles, with one right angle on each of <math>X</math>, <math>Y</math>, and <math>Z</math>.  
+
Now, if we look at the figure, we can see that the complement of the hexagon we are trying to find is composed of <math>3</math> isosceles trapezoids (namely <math>AXZF,CYXB,</math> and <math>EZYD</math>) and <math>3</math> right triangles (namely <math>\triangle XPN,\triangle YQO,</math> and <math>\triangle ZRM</math>).
−
Finding the trapezoid's area, we know that one base of each trapezoid is just the side length of the hexagon, which is <math>1</math>, and the other base is <math>\frac{3}{2}</math> (it is halfway in between the side and the longest diagonal, which has length <math>2</math>) with a height of <math>\frac{\sqrt{3}}{4}</math> (by using the Pythagorean Theorem and the fact that it is an isosceles trapezoid) to give each trapezoid having an area of <math>\frac{5\sqrt{3}}{16}</math> for a total area of <math>\frac{15\sqrt{3}}{16}.</math> (Alternatively, we could have calculated the area of hexagon <math>ABCDEF</math> and subtracted the area of <math>\triangle XYZ</math>, which, as we showed before, had a side length of <math>\frac{3}{2}</math>).  
+
 
−
Now, we need to find the area of each of the small triangles, which, if we look at the triangle that has a vertex on <math>X</math>, is similar to the triangle with a base of <math>YC = 1/2.</math> Using similar triangles, we calculate the base to be <math>\frac{1}{4}</math> and the height to be <math>\frac{\sqrt{3}}{4}</math> giving us an area of  <math>\frac{\sqrt{3}}{32}</math> per triangle, and a total area of <math>3\frac{\sqrt{3}}{32}</math>. Adding the two areas together, we get <math>\frac{15\sqrt{3}}{16} + \frac{3\sqrt{3}}{32} = \frac{33\sqrt{3}}{32}</math>. Finding the total area, we get <math>6 \cdot 1^2 \cdot \frac{\sqrt{3}}{4}=\frac{3\sqrt{3}}{2}</math>. Taking the complement, we get <math>\frac{3\sqrt{3}}{2} - \frac{33\sqrt{3}}{32} = \boxed{\textbf{(C)}\ \frac {15}{32}\sqrt{3}}.</math>
+
Finding the trapezoid's area, we know that one base of each trapezoid is just the side length of the hexagon, which is <math>1,</math> and the other base is <math>\frac{3}{2}</math> (it is halfway in between the side and the longest diagonal, which has length <math>2</math>) with a height of <math>\frac{\sqrt{3}}{4}</math> (by using the Pythagorean Theorem and the fact that it is an isosceles trapezoid) to give each trapezoid having an area of <math>\frac{5\sqrt{3}}{16}</math> for a total area of <math>\frac{15\sqrt{3}}{16}.</math> (Alternatively, we could have calculated the area of hexagon <math>ABCDEF</math> and subtracted the area of <math>\triangle XYZ,</math> which, as we showed before, had a side length of <math>\frac{3}{2}</math>).
 +
 
 +
Now, we need to find the area of each of the small triangles, which, if we look at the triangle that has a vertex on <math>X,</math> is similar to the triangle with a base of <math>YC = \frac12.</math> Using similar triangles, we calculate the base to be <math>\frac{1}{4}</math> and the height to be <math>\frac{\sqrt{3}}{4}</math> giving us an area of  <math>\frac{\sqrt{3}}{32}</math> per triangle, and a total area of <math>\frac{3\sqrt{3}}{32}.</math> Adding the two areas together, we get <math>\frac{15\sqrt{3}}{16} + \frac{3\sqrt{3}}{32} = \frac{33\sqrt{3}}{32}.</math> Finding the total area, we get <math>6 \cdot 1^2 \cdot \frac{\sqrt{3}}{4}=\frac{3\sqrt{3}}{2}.</math> Taking the complement, we get <math>\frac{3\sqrt{3}}{2} - \frac{33\sqrt{3}}{32} = \boxed{\textbf{(C)}\ \frac {15}{32}\sqrt{3}}.</math>
  
 
==Solution 4 (Trig)==
 
==Solution 4 (Trig)==

Revision as of 18:03, 21 October 2021

The following problem is from both the 2018 AMC 12B #20 and 2018 AMC 10B #24, so both problems redirect to this page.

Problem

Let $ABCDEF$ be a regular hexagon with side length $1$. Denote by $X$, $Y$, and $Z$ the midpoints of sides $\overline {AB}$, $\overline{CD}$, and $\overline{EF}$, respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of $\triangle ACE$ and $\triangle XYZ$?

$\textbf{(A)}\ \frac {3}{8}\sqrt{3} \qquad \textbf{(B)}\ \frac {7}{16}\sqrt{3} \qquad \textbf{(C)}\ \frac {15}{32}\sqrt{3} \qquad \textbf{(D)}\ \frac {1}{2}\sqrt{3} \qquad \textbf{(E)}\ \frac {9}{16}\sqrt{3}$

Diagram

[asy] /* Made by MRENTHUSIASM */ size(200); draw(polygon(6)); pair A, B, C, D, E, F, X, Y, Z, M, N, O, P, Q, R; A = dir(120); B = dir(60); C = dir(0); D = dir(300); E = dir(240); F = dir(180); X = midpoint(A--B); Y = midpoint(C--D); Z = midpoint(E--F); M = intersectionpoint(A--E,X--Z); N = intersectionpoint(A--C,X--Y); O = intersectionpoint(C--E,Y--Z); P = intersectionpoint(A--C,X--Z); Q = intersectionpoint(C--E,X--Y); R = intersectionpoint(A--E,Y--Z); fill(M--P--N--Q--O--R--cycle,mediumgray); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); dot("$E$",E,1.5*dir(E),linewidth(4)); dot("$F$",F,1.5*dir(F),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); dot(M^^N^^O^^P^^Q^^R,linewidth(4)); draw(A--C--E--cycle^^X--Y--Z--cycle); [/asy] ~MRENTHUSIASM

Solution 1 (Area Addition)

[asy] /* Made by MRENTHUSIASM */ size(200); draw(polygon(6)); pair A, B, C, D, E, F, X, Y, Z, M, N, O, P, Q, R; A = dir(120); B = dir(60); C = dir(0); D = dir(300); E = dir(240); F = dir(180); X = midpoint(A--B); Y = midpoint(C--D); Z = midpoint(E--F); M = intersectionpoint(A--E,X--Z); N = intersectionpoint(A--C,X--Y); O = intersectionpoint(C--E,Y--Z); P = intersectionpoint(A--C,X--Z); Q = intersectionpoint(C--E,X--Y); R = intersectionpoint(A--E,Y--Z); fill(M--P--N--Q--O--R--cycle,mediumgray); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); dot("$E$",E,1.5*dir(E),linewidth(4)); dot("$F$",F,1.5*dir(F),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); dot("$M$",M,1.5*dir(165),linewidth(4)); dot("$N$",N,1.5*dir(45),linewidth(4)); dot("$O$",O,1.5*dir(-75),linewidth(4)); dot("$P$",P,1.5*dir(105),linewidth(4)); dot("$Q$",Q,1.5*dir(-15),linewidth(4)); dot("$R$",R,1.5*dir(-135),linewidth(4)); draw(A--C--E--cycle^^X--Y--Z--cycle); draw(M--N--O--cycle,dashed); [/asy]

The desired area (hexagon $MPNQOR$) consists of an equilateral triangle ($\triangle MNO$) and three right triangles ($\triangle MPN,\triangle NQO,$ and $\triangle ORM$).

Notice that $\overline {AD}$ (not shown) and $\overline {BC}$ are parallel. $\overline {XY}$ divides transversals $\overline {AB}$ and $\overline {CD}$ into a $1:1$ ratio. (Note from Williamgolly: you can see this with similar triangles.) Thus, it must also divide transversal $\overline {AC}$ and transversal $\overline {CO}$ into a $1:1$ ratio. By symmetry, the same applies for $\overline {CE}$ and $\overline {EA}$ as well as $\overline {EM}$ and $\overline {AN}.$

In $\triangle ACE,$ we see that $\frac{[MNO]}{[ACE]} = \frac{1}{4}$ and $\frac{[MPN]}{[ACE]} = \frac{1}{8}.$ Our desired area becomes \[\left(\frac{1}{4}+3 \cdot \frac{1}{8}\right) \cdot \frac{\left(\sqrt{3}\right)^2 \cdot \sqrt{3}}{4} = \frac {15}{32}\sqrt{3} = \boxed{\textbf{(C)}\ \frac {15}{32}\sqrt{3}}.\]

Solution 2 (Area Subtraction)

Instead of directly finding the desired hexagonal area, $\triangle XYZ$ can be found. It consists of three triangles and the desired hexagon. Given triangle rotational symmetry, the three triangles are congruent. See that $\triangle XYZ$ and $\triangle ACE$ are equilateral, so $m\angle PXN=60,$ so $m\angle AXP = \frac{180-60}{2}=60.$ As $\overline {AC}$ is a transversal running through $\overline {FC}$ (use your imagination) and $\overline {AB},$ we have $m\angle BAC=m\angle FCA = \frac{m\angle ACE}{2}=30.$

Then, $\triangle APX$ is a $30$-$60$-$90$ triangle. By HL congruence, $\triangle APX \cong \triangle NPX.$ Note that $AX=\frac{1}{2}.$ Then, the area of $\triangle PXN$ is $\frac{\sqrt{3}}{32}.$ There are three such triangles for a total area of $\triangle XYZ$ is $\frac{3\sqrt{3}}{32}.$ Find the side of $\triangle XYZ$ to be $\frac{3}{2},$ so the area is $\frac{9\sqrt{3}}{16}.$

The answer is \[\frac{9\sqrt{3}}{16}-\frac{3\sqrt{3}}{32}=\boxed{\textbf{(C)}\ \frac {15}{32}\sqrt{3}}.\] ~BJHHar

Solution 3 (Area Subtraction)

[asy] /* Made by MRENTHUSIASM */ size(200); draw(polygon(6)); pair A, B, C, D, E, F, X, Y, Z, M, N, O, P, Q, R; A = dir(120); B = dir(60); C = dir(0); D = dir(300); E = dir(240); F = dir(180); X = midpoint(A--B); Y = midpoint(C--D); Z = midpoint(E--F); M = intersectionpoint(A--E,X--Z); N = intersectionpoint(A--C,X--Y); O = intersectionpoint(C--E,Y--Z); P = intersectionpoint(A--C,X--Z); Q = intersectionpoint(C--E,X--Y); R = intersectionpoint(A--E,Y--Z); fill(M--P--N--Q--O--R--cycle,mediumgray); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); dot("$E$",E,1.5*dir(E),linewidth(4)); dot("$F$",F,1.5*dir(F),linewidth(4)); dot("$X$",X,1.5*dir(X),linewidth(4)); dot("$Y$",Y,1.5*dir(Y),linewidth(4)); dot("$Z$",Z,1.5*dir(Z),linewidth(4)); dot("$M$",M,1.5*dir(165),linewidth(4)); dot("$N$",N,1.5*dir(45),linewidth(4)); dot("$O$",O,1.5*dir(-75),linewidth(4)); dot("$P$",P,1.5*dir(105),linewidth(4)); dot("$Q$",Q,1.5*dir(-15),linewidth(4)); dot("$R$",R,1.5*dir(-135),linewidth(4)); draw(A--C--E--cycle^^X--Y--Z--cycle); draw(M--N--O--cycle,dashed); [/asy]

Now, if we look at the figure, we can see that the complement of the hexagon we are trying to find is composed of $3$ isosceles trapezoids (namely $AXZF,CYXB,$ and $EZYD$) and $3$ right triangles (namely $\triangle XPN,\triangle YQO,$ and $\triangle ZRM$).

Finding the trapezoid's area, we know that one base of each trapezoid is just the side length of the hexagon, which is $1,$ and the other base is $\frac{3}{2}$ (it is halfway in between the side and the longest diagonal, which has length $2$) with a height of $\frac{\sqrt{3}}{4}$ (by using the Pythagorean Theorem and the fact that it is an isosceles trapezoid) to give each trapezoid having an area of $\frac{5\sqrt{3}}{16}$ for a total area of $\frac{15\sqrt{3}}{16}.$ (Alternatively, we could have calculated the area of hexagon $ABCDEF$ and subtracted the area of $\triangle XYZ,$ which, as we showed before, had a side length of $\frac{3}{2}$).

Now, we need to find the area of each of the small triangles, which, if we look at the triangle that has a vertex on $X,$ is similar to the triangle with a base of $YC = \frac12.$ Using similar triangles, we calculate the base to be $\frac{1}{4}$ and the height to be $\frac{\sqrt{3}}{4}$ giving us an area of $\frac{\sqrt{3}}{32}$ per triangle, and a total area of $\frac{3\sqrt{3}}{32}.$ Adding the two areas together, we get $\frac{15\sqrt{3}}{16} + \frac{3\sqrt{3}}{32} = \frac{33\sqrt{3}}{32}.$ Finding the total area, we get $6 \cdot 1^2 \cdot \frac{\sqrt{3}}{4}=\frac{3\sqrt{3}}{2}.$ Taking the complement, we get $\frac{3\sqrt{3}}{2} - \frac{33\sqrt{3}}{32} = \boxed{\textbf{(C)}\ \frac {15}{32}\sqrt{3}}.$

Solution 4 (Trig)

Notice, the area of the convex hexagon formed through the intersection of the $2$ triangles can be found by finding the area of the triangle formed by the midpoints of the sides and subtracting the smaller triangles that are formed by the region inside this triangle but outside the other triangle. First, let's find the area of the triangle formed by the midpoint of the sides. Notice, this is an equilateral triangle, thus all we need is to find the length of its side. To do this, we look at the isosceles trapezoid outside this triangle but inside the outer hexagon. Since the interior angle of a regular hexagon is $120^{\textrm{o}}$ and the trapezoid is isosceles, we know that the angle opposite is $60^{\textrm{o}}$, and thus the side length of this triangle is $1+2(\frac{1}{2}\cos(60^{\textrm{o}})=1+\frac{1}{2}=\frac{3}{2}$. So the area of this triangle is $\frac{\sqrt{3}}{4}s^2=\frac{9\sqrt{3}}{16}$.

Now let's find the area of the smaller triangles. Notice, triangle $ACE$ cuts off smaller isosceles triangles from the outer hexagon. The base of these isosceles triangles is perpendicular to the base of the isosceles trapezoid mentioned before, thus we can use trigonometric ratios to find the base and height of these smaller triangles, which are all congruent due to the rotational symmetry of a regular hexagon. The area is then $\frac{1}{2}(\frac{1}{2})\cos(60^{\textrm{o}}))(\frac{1}{2}\sin(60^{\textrm{o}}))=\frac{\sqrt{3}}{32}$ and the sum of the areas is $3\cdot \frac{\sqrt{3}}{32}=\frac{3\sqrt{3}}{32}$.

Therefore, the area of the convex hexagon is $\frac{9\sqrt{3}}{16}-\frac{3\sqrt{3}}{32}=\frac{18\sqrt{3}}{32}-\frac{3\sqrt{3}}{32}=\boxed{\textbf{(C)}\ \frac {15}{32}\sqrt{3}}$.

Solution 5

Dividing $\triangle MNO$ into two right triangles congruent to $\triangle PMN$, we see that $[MPNQOR]=\dfrac{5}{8}[ACE]$. Because $[ACE] = \dfrac{1}{2}[ABCDEF]$, we have $[MPNQOR]=\dfrac{5}{16}[ABCDEF]$. From here, you should be able to tell that the answer will have a factor of $5$, and $\boxed{\textbf{(C)} \frac {15}{32}\sqrt{3}}$ is the only answer that has a factor of $5$. However, if you want to actually calculate the area, you would calculate $[ABCDEF]$ to be $6 \cdot \dfrac{\sqrt{3}}{2 \cdot 2} = \dfrac{3\sqrt{3}}{2}$, so $[MPNQOR] = \dfrac{5}{16} \cdot \dfrac{3\sqrt{3}}{2} = \boxed{\textbf{(C)}\ \frac {15}{32}\sqrt{3}}$.

Solution 6 (Least Algebra Needed)

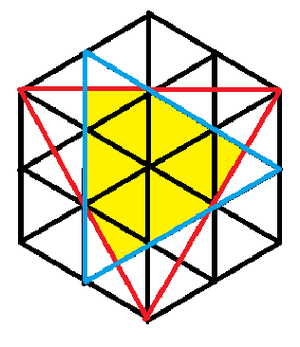
Billybobjoe.png

We can see by the picture that there are a total of 24 small equilateral triangles in the hexagon, each with the same area(Look at the black lines). In the yellow region, there are 6 full triangles, and 3 half triangles, giving us 7.5 triangles worth of area. Thus, area of the region we want is $\frac{7.5}{24}$ of the entire hexagon. The total area of the hexagon is $\frac{3\sqrt{3}}{2}$, so our answer is $\frac{7.5}{24} \cdot \frac{3\sqrt{3}}{2}$ = $\boxed{(C) \frac{15\sqrt{3}}{32}}$

-AlexLikeMath

Solution 7

If we try to coordinate bash this problem, it's going to look very ugly with a lot of radicals. However, we can alter and skew the diagram in such a way that all ratios of lengths and areas stay the same while making it a lot easier to work with. Then, we can find the ratio of the area of the wanted region to the area of $ABCDEF$ then apply it to the old diagram. [asy] unitsize(1cm); draw((0,0)--(4,0)--(6,3.464)--(2,3.464)--(0,0)); draw((2,0)--(1,1.732)); draw((5,1.732)--(4,3.464)); draw((1.5, 0.866)--(3, 3.464)--(4.5, 0.866)--cycle); draw((2,0)--(2,3.464)--(5,1.732)--cycle); [/asy]

[asy] unitsize(1cm); draw((1,0)--(1,4),gray(.7)); draw((2,0)--(2,4),gray(.7)); draw((3,0)--(3,4),gray(.7)); draw((0,1)--(4,1),gray(.7)); draw((0,2)--(4,2),gray(.7)); draw((0,3)--(4,3),gray(.7)); draw((0,0)--(4,0)--(4,4)--(0,4)--(0,0)); draw((2,0)--(0,2)); draw((4,2)--(2,4)); draw((1,1)--(1,4)--(4,1)--cycle); draw((0,4)--(2,0)--(4,2)--cycle); fill((1,4)--(1,3.5)--(2,3)--cycle,red); fill((1,1)--(1.5,1)--(1,2)--cycle,red); fill((3,1)--(3.5,1.5)--(4,1)--cycle,red); [/asy]

The isosceles right triangle with a leg length of $3$ in the new diagram is $\triangle XYZ$ in the old diagram. We see that if we want to take the area of the new hexagon, we must subtract $\frac{3}{4}$ from the area of $\triangle XYZ$ (the red triangles), giving us $\frac{15}{4}$. However, we need to take the ratio of this area to the area of $ABCDEF$, which is $\frac{\frac{15}{4}}{12}=\frac{5}{16}$. Now we know that our answer is $\frac{5}{16} \cdot \frac{3\sqrt{3}}{2}=\boxed{\textbf{(C)}\ \frac {15}{32}\sqrt{3}}$.

Video Solution

https://www.youtube.com/watch?v=yDbn9Mx2myw

See Also

2018 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 23 		Followed by
Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2018 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2018_AMC_10B_Problems/Problem_24&oldid=163879"