Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AMC 12B Problems/Problem 25"

m (→‎Supplement (Calculating sin54/cos36 from Scratch))
m (→‎Supplement (Calculating sin54/cos36 from Scratch))
Line 135: Line 135:
  
 
==Supplement (Calculating sin54/cos36 from Scratch)==
 
==Supplement (Calculating sin54/cos36 from Scratch)==
 +
 +
Method 1:
  
 
[[File:2023AMC12BP25.png|center|250px]]
 
[[File:2023AMC12BP25.png|center|250px]]
  
−
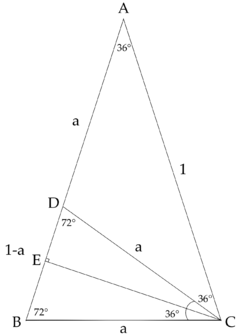
Construct <math>\triangle ABC</math> with <math>\angle A = 36^{\circ}</math>, <math>\angle B = \angle C = 72^{\circ}</math> and <math>\triangle BCD</math> with <math>\angle C = 36^{\circ}</math>, <math>\angle DBC = \angle BDC = 72^{\circ}</math>. WLOG, let <math>AC = 1</math>, <math>BC = CD = AD = a</math>, <math>BD = 1-a</math>.
+
Construct golden ratio <math>\triangle ABC</math> with <math>\angle A = 36^{\circ}</math>, <math>\angle B = \angle C = 72^{\circ}</math> and <math>\triangle BCD</math> with <math>\angle C = 36^{\circ}</math>, <math>\angle DBC = \angle BDC = 72^{\circ}</math>. WLOG, let <math>AB = AC = 1</math>, <math>BC = CD = AD = a</math>, <math>BD = 1-a</math>. <math>\triangle ABC \sin \triangle BCD</math>
  
 
<cmath>\frac{AC}{BC} = \frac{BC}{BD}, \quad \frac{1}{a} = \frac{a}{1-a}, \quad 1-a=a^2, \quad a^2 + a - 1 = 0</cmath>
 
<cmath>\frac{AC}{BC} = \frac{BC}{BD}, \quad \frac{1}{a} = \frac{a}{1-a}, \quad 1-a=a^2, \quad a^2 + a - 1 = 0</cmath>
Line 147: Line 149:
  
 
<cmath>\sin 54^{\circ} = \cos 36^{\circ} = \frac{ \sqrt{5} + 1 }{4}</cmath>
 
<cmath>\sin 54^{\circ} = \cos 36^{\circ} = \frac{ \sqrt{5} + 1 }{4}</cmath>
 +
 +
Method 2:
 +
(Writing in progress...)
  
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]

Revision as of 09:19, 16 November 2023

The following problem is from both the 2023 AMC 10B #25 and 2023 AMC 12B #25, so both problems redirect to this page.

Problem

A regular pentagon with area $\sqrt{5}+1$ is printed on paper and cut out. The five vertices of the pentagon are folded into the center of the pentagon, creating a smaller pentagon. What is the area of the new pentagon?

$\textbf{(A)}~4-\sqrt{5}\qquad\textbf{(B)}~\sqrt{5}-1\qquad\textbf{(C)}~8-3\sqrt{5}\qquad\textbf{(D)}~\frac{\sqrt{5}+1}{2}\qquad\textbf{(E)}~\frac{2+\sqrt{5}}{3}$


Solution 1

Pentagon 2023 12B Q25 dissmo.png

Let the original pentagon be $ABCDE$ centered at $O$. The dashed lines represent the fold lines. WLOG, let's focus on vertex $A$.

Since $A$ is folded onto $O$, $AN = NO$ where $N$ is the intersection of $AO$ and the creaseline between $A$ and $O$. Note that the inner pentagon is regular, and therefore similar to the original pentagon, due to symmetry.

Because of their similarity, the ratio of the inner pentagon's area to that of the outer pentagon can be represented by

$(\frac{ON}{OM})^{2} = (\frac{\frac{OA}{2}}{OA\sin (\angle OAE)})^{2} = \frac{1}{4\sin^{2}54}$


Option 1: Knowledge

Remember that $\sin54 = \frac{1+\sqrt5}{4}$.


Option 2: Angle Identities

$\sin54 = \cos36$

$4\cos^{3}18-3\cos18 = 2\sin18\cos18$

$4(1-\sin^{2}18)-3-2\sin18=0$

$4\sin^{2}18+2\sin18-1=0$

$\sin18 = \frac{-1+\sqrt5}{4}$

$\sin54 = \cos36 = 1-2\sin^{2}18 = \frac{1+\sqrt5}{4}$


$\sin^{2}54 =\frac{3+\sqrt5}{8}$

Let the inner pentagon be $Z$.

$[Z] = \frac{1}{4\sin^{2}54}[ABCDE]$

$= \frac{2(1+\sqrt5)}{3+\sqrt5}$

$= \sqrt5-1$

$\boxed{B}$

-Dissmo

Solution 2

[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); // Draw the larger pentagon draw(A--B--C--D--E--cycle); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); draw(AA--OO, blue); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); draw(OOO--OAO,green); dot(O); dot((O+A)/2); label("$r_b$", (O+A)*.7, E,blue); label("$a_s$", (O+A)*.2 +(0+0.18,0.05), E,green); label("$r_s$", O+(-0.175,0.2), E,pink); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); // Draw the smaller pentagon draw(F--G--H--I--J--cycle,red); draw(arc(O,(H+I)*.5*.6,H*.6)); label("$36^\circ$",O+(+0.05,0.15),NW); draw(O--H,pink); [/asy]

Let $r_b$ and $r_s$ be the circumradius of the big and small pentagon, respectively. Let $a_s$ be the apothem of the smaller pentagon and $A_s$ and $A_b$ be the areas of the smaller and larger pentagon, respectively.

From the diagram: \begin{align*} \cos{36^\circ} &= \dfrac{a_s}{r_s} = \dfrac{\phi}{2} = \dfrac{\sqrt{5}+1}{4}\\ a_s &= \dfrac{r_b}{2}\\ A_s &= \left(\dfrac{r_s}{r_b}\right)^2A_b\\ &=\left(\dfrac{a_s}{\cos{36^\circ} r_b}\right)^2 \left(1+\sqrt{5}\right)\\ &=\left(\dfrac{r_b}{\dfrac{\phi}{2} r_b}\right)^2 \left(1+\sqrt{5}\right)\\ &=\left(\dfrac{1}{2 \dfrac{\phi}{2}}\right)^2 \left(1+\sqrt{5}\right)\\ &=\left(\dfrac{2}{\sqrt{5}+1}\right)^2 \left(1+\sqrt{5}\right)\\ &=\dfrac{4}{\sqrt{5}+1} \\ &=\dfrac{4\left(\sqrt{5}-1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)} \\ &=\sqrt{5}-1 \end{align*} \[\boxed{\textbf{(B) }\sqrt{5}-1}\] ~Technodoggo

Solution 3

Interestingly, we find that the pentagon we need is the one that is represented by the intersection of the diagonals. Through similar triangles and the golden ratio, we find that the side length ratio of the two pentagons is $\frac{\sqrt{5}-1}{2}$ Thus, the answer is $\sqrt{5}+1 \cdot (\frac{\sqrt{5}-1}{2})^2 = \sqrt{5}-1$. $\boxed{\text{B}}$ ~andliu766

Supplement (Calculating sin54/cos36 from Scratch)

Method 1:

2023AMC12BP25.png

Construct golden ratio $\triangle ABC$ with $\angle A = 36^{\circ}$, $\angle B = \angle C = 72^{\circ}$ and $\triangle BCD$ with $\angle C = 36^{\circ}$, $\angle DBC = \angle BDC = 72^{\circ}$. WLOG, let $AB = AC = 1$, $BC = CD = AD = a$, $BD = 1-a$. $\triangle ABC \sin \triangle BCD$

\[\frac{AC}{BC} = \frac{BC}{BD}, \quad \frac{1}{a} = \frac{a}{1-a}, \quad 1-a=a^2, \quad a^2 + a - 1 = 0\]

\[a = \frac{ -1 + \sqrt{1^2 - 4(-1) } }{2} = \frac{ \sqrt{5} -1 }{2}\]

\[\cos 36^{\circ} = \cos \angle A = \frac{AE}{AC} = \frac{ 1-a }{2} + 1 = \frac{ a + 1 }{2} = \frac{ \frac{ \sqrt{5} -1 }{2} + 1 }{2} = \frac{ \sqrt{5} + 1 }{4}\]

\[\sin 54^{\circ} = \cos 36^{\circ} = \frac{ \sqrt{5} + 1 }{4}\]

Method 2: (Writing in progress...)

~isabelchen

Video Solution 1 by SpreadTheMathLove

https://www.youtube.com/watch?v=ROVjN3oYLbQ

Video Solution 2 by OmegaLearn

https://youtu.be/_WztOIk_2Q8


See also

2023 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AMC_12B_Problems/Problem_25&oldid=203920"