Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2019 AMC 10B Problems/Problem 23"

(→‎Solution 3)
 
(46 intermediate revisions by 25 users not shown)
Line 1: Line 1:
−
{{duplicate|[[2019 AMC 10B Problems|2019 AMC 10B #23]] and [[2019 AMC 12B Problems|2019 AMC 12B #20]]}}
+
{{duplicate|[[2019 AMC 10B Problems#Problem 23|2019 AMC 10B #23]] and [[2019 AMC 12B Problems#Problem 20|2019 AMC 12B #20]]}}
  
 
==Problem==
 
==Problem==
  
−
Points <math>A(6,13)</math> and <math>B(12,11)</math> lie on circle <math>\omega</math> in the plane. Suppose that the tangent lines to <math>\omega</math> at <math>A</math> and <math>B</math> intersect at a point on the <math>x</math>-axis. What is the area of <math>\omega</math>?
+
Points <math>A=(6,13)</math> and <math>B=(12,11)</math> lie on circle <math>\omega</math> in the plane. Suppose that the tangent lines to <math>\omega</math> at <math>A</math> and <math>B</math> intersect at a point on the <math>x</math>-axis. What is the area of <math>\omega</math>?
  
 
<math>\textbf{(A) }\frac{83\pi}{8}\qquad\textbf{(B) }\frac{21\pi}{2}\qquad\textbf{(C) }
 
<math>\textbf{(A) }\frac{83\pi}{8}\qquad\textbf{(B) }\frac{21\pi}{2}\qquad\textbf{(C) }
Line 9: Line 9:
  
 
==Solution 1==
 
==Solution 1==
−
First, observe that the two tangent lines are of identical length. Therefore, suppose the intersection was <math>(x, 0)</math>. Using Pythagorean Theorem gives <math>x=5</math>.
+
First, observe that the two tangent lines are of identical length. Therefore, supposing that the point of intersection is <math>(x, 0)</math>, the Pythagorean Theorem gives <math>\sqrt{(x-6)^2 + 13^2} = \sqrt{(x-12)^2 + 11^2}</math>. This simplifies to <math>x = 5</math>.
  
−
Notice (due to the right angles formed by a radius and its tangent line) that the quadrilateral (kite) defined by circle center, <math>A</math>, <math>B</math>, and <math>(5, 0)</math> form a cyclic quadrilateral. Therefore, we can use Ptolemy's theorem:
+
Further, notice (due to the right angles formed by a radius and its tangent line) that the quadrilateral (a kite) <math>AOBX</math> is cyclic.  
  
−
<math>2\sqrt{170}x = d * \sqrt{40}</math>, where <math>d</math> represents the distance between circle center and <math>(5, 0)</math>. Therefore, <math>d = \sqrt{17}x</math>. Using Pythagorean Theorem on <math>(5, 0)</math>, either one of <math>A</math> or <math>B</math>, and the circle center, we realize that <math>170 + x^2 = 17x^2</math>, at which point <math>x^2 = \frac{85}{8}</math>, so the answer is <math>\boxed{\textbf{(C) }\frac{85}{8}\pi}</math>.
+
Therefore, we can apply [[Ptolemy's Theorem]] to give:
  
−
==Solution 2==
+
<math>2\sqrt{170}r = d \sqrt{40}</math>, where <math>r</math> is the radius of the circle and <math>d</math> is the distance between the circle's center and <math>(5, 0)</math>. Therefore, <math>d = \sqrt{17}r</math>.  
−
First, follow solution 1 and obtain <math>x=5</math>. Label the point <math>(5,0)</math> as point <math>C</math>. The midpoint <math>M</math> of segment <math>AB</math> is <math>(9, 12)</math>. Notice that the center of the circle must lie on the line that goes through the points <math>C</math> and <math>M</math>. Thus, the center of the circle lies on the line <math>y=3x-15</math>.  
 
  
−
Line <math>AC</math> is <math>y=13x-65</math>. The perpendicular line must pass through <math>A(6, 13)</math> and <math>(x, 3x-15)</math>. The slope of the perpendicular line is <math>-\frac{1}{13}</math>. The line is hence <math>y=-\frac{x}{13}+\frac{175}{13}</math>. The point <math>(x, 3x-15)</math> lies on this line. Therefore, <math>3x-15=-\frac{x}{13}+\frac{175}{13}</math>. Solving this equation tells us that <math>x=\frac{37}{4}</math>. So the center of the circle is <math>(\frac{37}{4}, \frac{51}{4})</math>. The distance between the center, <math>(\frac{37}{4}, \frac{51}{4})</math>, and point A is <math>\frac{\sqrt{170}}{4}</math>. Hence, the area is <math>\frac{85}{8}\pi</math>. The answer is <math>\boxed{\textbf{(C) }\frac{85}{8}\pi}</math>.
+
Using the Pythagorean Theorem on the right triangle <math>OAX</math> (or <math>OBX</math>), we find that <math>170 + r^2 = 17r^2</math>, so <math>r^2 = \frac{85}{8}</math>, and thus the area of the circle is <math>\boxed{\textbf{(C) }\frac{85}{8}\pi}</math>.
 +
 
 +
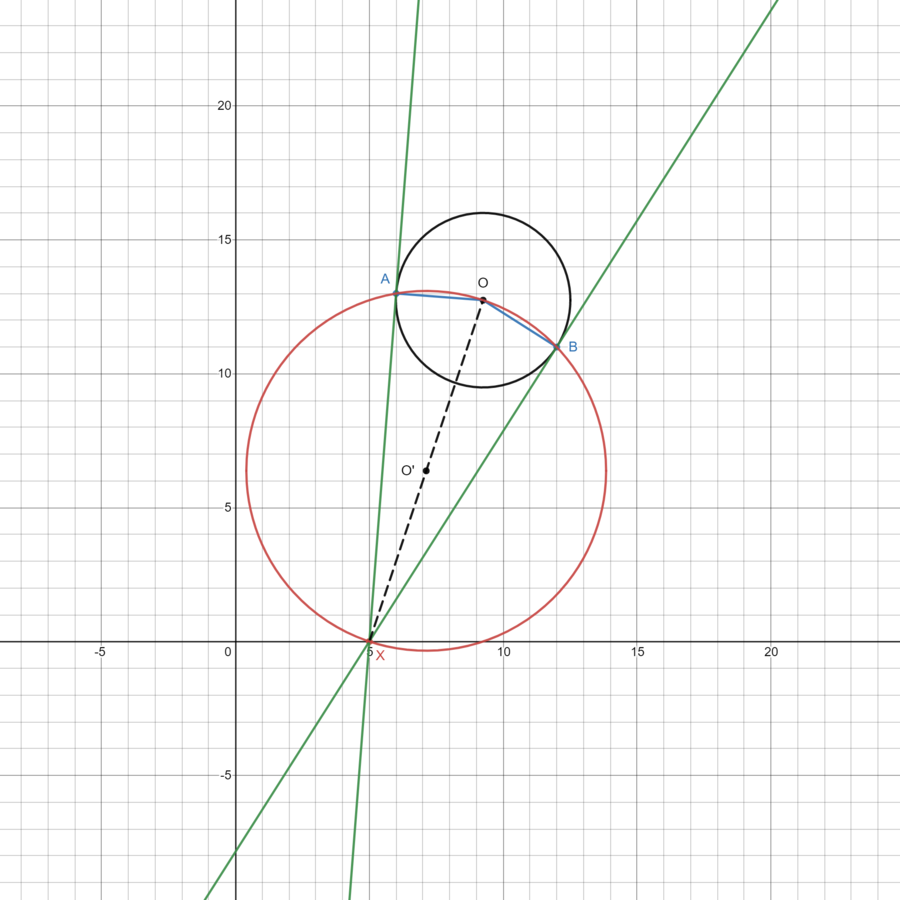
===Diagram for Solution 1===
 +
[[File:Desmos-graph (1).png|900px|caption]]
 +
 
 +
~BakedPotato66
 +
 
 +
==Solution 2 (coordinate bash)==
 +
We firstly obtain <math>x=5</math> as in Solution 1. Label the point <math>(5,0)</math> as <math>C</math>. The midpoint <math>M</math> of segment <math>AB</math> is <math>(9, 12)</math>. Notice that the center of the circle must lie on the line passing through the points <math>C</math> and <math>M</math>. Thus, the center of the circle lies on the line <math>y=3x-15</math>.  
 +
 
 +
Line <math>AC</math> is <math>y=13x-65</math>. Therefore, the slope of the line perpendicular to <math>AC</math> is <math>-\frac{1}{13}</math>, so its equation is <math>y=-\frac{x}{13}+\frac{175}{13}</math>.  
 +
 
 +
But notice that this line must pass through <math>A(6, 13)</math> and <math>(x, 3x-15)</math>. Hence <math>3x-15=-\frac{x}{13}+\frac{175}{13} \Rightarrow x=\frac{37}{4}</math>. So the center of the circle is <math>\left(\frac{37}{4}, \frac{51}{4}\right)</math>.  
 +
 
 +
Finally, the distance between the center, <math>\left(\frac{37}{4}, \frac{51}{4}\right)</math>, and point <math>A</math> is <math>\frac{\sqrt{170}}{4}</math>. Thus the area of the circle is <math>\boxed{\textbf{(C) }\frac{85}{8}\pi}</math>.
  
 
==Solution 3==
 
==Solution 3==
−
The mid point of <math>AB</math> is <math>D(9,12)</math>. Let the tangent lines at <math>A</math> and <math>B</math> intersect at <math>C(a,0)</math> on the <math>X</math> axis. Then <math>CD</math> would be the perpendicular bisector of <math>AB</math>. Let the center of circle be O. Then <math>\triangle AOC</math> is similar to <math>\triangle DAC</math>, that is <math>\frac{OA}{AC} = \frac{AD}{DC}.</math>
+
The midpoint of <math>AB</math> is <math>D(9,12)</math>. Let the tangent lines at <math>A</math> and <math>B</math> intersect at <math>C(a,0)</math> on the <math>x</math>-axis. Then <math>CD</math> is the perpendicular bisector of <math>AB</math>. Let the center of the circle be <math>O</math>. Then <math>\triangle AOC</math> is similar to <math>\triangle DAC</math>, so <math>\frac{OA}{AC} = \frac{AD}{DC}</math>.
−
The slope of <math>AB</math> is <math>\frac{13-11}{6-12}=\frac{-1}{3}</math>, therefore the slope of CD will be 3. The equation of <math>CD</math> is <math>y-12=3*(x-9)</math>, that is <math>y=3x-15</math>. Let <math>y=0</math>. Then we have <math>x=5</math>, which is the <math>x</math> coordinate of <math>C(5,0)</math>.
+
The slope of <math>AB</math> is <math>\frac{13-11}{6-12}=\frac{-1}{3}</math>, so the slope of <math>CD</math> is <math>3</math>. Hence, the equation of <math>CD</math> is <math>y-12=3(x-9) \Rightarrow y=3x-15</math>. Letting <math>y=0</math>, we have <math>x=5</math>, so <math>C = (5,0)</math>.
 +
 
 +
Now, we compute <math>AC=\sqrt{(6-5)^2+(13-0)^2}=\sqrt{170}</math>,
 +
<math>AD=\sqrt{(6-9)^2+(13-12)^2}=\sqrt{10}</math>, and
 +
<math>DC=\sqrt{(9-5)^2+(12-0)^2}=\sqrt{160}</math>.
 +
 
 +
Therefore <math>OA = \frac{AC\cdot AD}{DC}=\sqrt{\frac{85}{8}}</math>,
 +
and consequently, the area of the circle is <math>\pi\cdot OA^2 = \boxed{\textbf{(C) }\frac{85}{8}\pi}</math>.
 +
 
 +
 
 +
==Solution 4 (how fast can you multiply two-digit numbers?)==
 +
Let <math>(x,0)</math> be the intersection on the x-axis. By Power of a Point Theorem, <math>(x-6)^2+13^2=(x-12)^2+11^2\implies x=5</math>. Then the equations  for the tangent lines passing <math>A</math> and <math>B</math>, respectively, are <math>13(x-6)+13=y</math> and <math>\frac{11}{7}(x-12)+11=y</math>. Then the lines normal (perpendicular) to them are <math>-\frac{1}{13}(x-6)+13=y</math> and <math>-\frac{7}{11}(x-12)+11=y</math>. Solving for <math>x</math>, we have
 +
 
 +
 
 +
 
 +
<cmath>-\frac{7}{11}(x-12)+11=-\frac{1}{13}(x-6)+13</cmath>
 +
<cmath>\frac{13\cdot7x-11x}{13\cdot11}=\frac{84\cdot13-6\cdot11-2\cdot11\cdot13}{11\cdot13}</cmath>
 +
<cmath>13\cdot7x-11x=84\cdot13-6\cdot11-2\cdot11\cdot13</cmath>
 +
 
 +
After condensing, <math>x=\frac{37}{4}</math>. Then, the center of <math>\omega</math> is <math>\left(\frac{37}{4}, \frac{51}{4}\right)</math>. Apply distance formula. WLOG, assume you use <math>A</math>. Then, the area of <math>\omega</math> is <cmath>\left(\sqrt{\frac{1^2}{4^2}+\frac{13^2}{4^2}}\right)^2\pi=\frac{170\pi}{16} \implies \boxed{\textbf{(C) }\frac{85}{8}\pi}.</cmath>
 +
 
 +
==Solution 5 (tangent cheese)==
 +
After getting <math>x=5</math>, let <math>C=(5,0)</math>. Get the slopes of the lines <math>AC</math> and <math>BC</math>, namely <math>\frac{13}{6-5}=13</math>, <math>\frac{11}{12-5}=\frac{11}{7}</math>. Then, use tangent angle subtraction to get <math>\tan{2x}=\frac{13-\frac{11}{7}}{1+13*\frac{11}{7}}=\frac{80}{150}=\frac{8}{15}</math>. Then, apply tangent double angle to get <math>\tan{2x}=\frac{8}{15}=\frac{2\tan{x}}{1-\tan^2{x}}</math>. Solving, we obtain <math>\tan{x}=\frac{1}{4}</math>. Then, note that <math>\tan{x}=r/{BC}</math>, so <math>r=\frac{1}{4}*\sqrt{170}</math>. Finishing off, we obtain <math>A=\pi*r^2=\pi*170/16=\boxed{\textbf{(C) }\frac{85}{8}\pi}</math>.
 +
 
 +
~SigmaPiE
 +
 
 +
==Video Solution==
 +
For those who want a video solution: (Is similar to Solution 1)
 +
https://youtu.be/WI2NVuIp1Ik
 +
 
 +
==Video Solution by TheBeautyofMath==
 +
https://youtu.be/W1zuqrTlBtU
 +
 
 +
~IceMatrix
 +
==Video Solution by The Power of Logic==
 +
https://www.youtube.com/watch?v=sQIWSrio_Hc
  
−
<math>AC=\sqrt{(6-5)^2+(13-0)^2}=\sqrt{170}</math>,
+
~The Power of Logic
−
<math>AD=\sqrt{(6-9)^2)+(13-12)^2}=\sqrt{10}</math>,
 
−
<math>DC=\sqrt{(9-5)^2+(12-0)^2}=\sqrt{160}</math>,
 
−
Therefore <math>OA = \frac{AC*AD}{DC}=\sqrt{\frac{85}{8}}</math>,
 
−
Consequently, the area of the circle is <math>pi* OA^2 = pi*\frac{85}{8}</math>.
 
−
(by Zhen Qin)
 
−
(P.S. Will someone please Latex this?)
 
−
(<math>\LaTeX</math>ed by a pewdiepie subscriber)
 
  
 
==See Also==
 
==See Also==
Line 37: Line 78:
 
{{AMC12 box|year=2019|ab=B|num-b=19|num-a=21}}
 
{{AMC12 box|year=2019|ab=B|num-b=19|num-a=21}}
 
{{MAA Notice}}
 
{{MAA Notice}}
−
SUB2PEWDS
 

Latest revision as of 09:25, 20 December 2023

The following problem is from both the 2019 AMC 10B #23 and 2019 AMC 12B #20, so both problems redirect to this page.

Problem

Points $A=(6,13)$ and $B=(12,11)$ lie on circle $\omega$ in the plane. Suppose that the tangent lines to $\omega$ at $A$ and $B$ intersect at a point on the $x$-axis. What is the area of $\omega$?

$\textbf{(A) }\frac{83\pi}{8}\qquad\textbf{(B) }\frac{21\pi}{2}\qquad\textbf{(C) } \frac{85\pi}{8}\qquad\textbf{(D) }\frac{43\pi}{4}\qquad\textbf{(E) }\frac{87\pi}{8}$

Solution 1

First, observe that the two tangent lines are of identical length. Therefore, supposing that the point of intersection is $(x, 0)$, the Pythagorean Theorem gives $\sqrt{(x-6)^2 + 13^2} = \sqrt{(x-12)^2 + 11^2}$. This simplifies to $x = 5$.

Further, notice (due to the right angles formed by a radius and its tangent line) that the quadrilateral (a kite) $AOBX$ is cyclic.

Therefore, we can apply Ptolemy's Theorem to give:

$2\sqrt{170}r = d \sqrt{40}$, where $r$ is the radius of the circle and $d$ is the distance between the circle's center and $(5, 0)$. Therefore, $d = \sqrt{17}r$.

Using the Pythagorean Theorem on the right triangle $OAX$ (or $OBX$), we find that $170 + r^2 = 17r^2$, so $r^2 = \frac{85}{8}$, and thus the area of the circle is $\boxed{\textbf{(C) }\frac{85}{8}\pi}$.

Diagram for Solution 1

caption

~BakedPotato66

Solution 2 (coordinate bash)

We firstly obtain $x=5$ as in Solution 1. Label the point $(5,0)$ as $C$. The midpoint $M$ of segment $AB$ is $(9, 12)$. Notice that the center of the circle must lie on the line passing through the points $C$ and $M$. Thus, the center of the circle lies on the line $y=3x-15$.

Line $AC$ is $y=13x-65$. Therefore, the slope of the line perpendicular to $AC$ is $-\frac{1}{13}$, so its equation is $y=-\frac{x}{13}+\frac{175}{13}$.

But notice that this line must pass through $A(6, 13)$ and $(x, 3x-15)$. Hence $3x-15=-\frac{x}{13}+\frac{175}{13} \Rightarrow x=\frac{37}{4}$. So the center of the circle is $\left(\frac{37}{4}, \frac{51}{4}\right)$.

Finally, the distance between the center, $\left(\frac{37}{4}, \frac{51}{4}\right)$, and point $A$ is $\frac{\sqrt{170}}{4}$. Thus the area of the circle is $\boxed{\textbf{(C) }\frac{85}{8}\pi}$.

Solution 3

The midpoint of $AB$ is $D(9,12)$. Let the tangent lines at $A$ and $B$ intersect at $C(a,0)$ on the $x$-axis. Then $CD$ is the perpendicular bisector of $AB$. Let the center of the circle be $O$. Then $\triangle AOC$ is similar to $\triangle DAC$, so $\frac{OA}{AC} = \frac{AD}{DC}$. The slope of $AB$ is $\frac{13-11}{6-12}=\frac{-1}{3}$, so the slope of $CD$ is $3$. Hence, the equation of $CD$ is $y-12=3(x-9) \Rightarrow y=3x-15$. Letting $y=0$, we have $x=5$, so $C = (5,0)$.

Now, we compute $AC=\sqrt{(6-5)^2+(13-0)^2}=\sqrt{170}$, $AD=\sqrt{(6-9)^2+(13-12)^2}=\sqrt{10}$, and $DC=\sqrt{(9-5)^2+(12-0)^2}=\sqrt{160}$.

Therefore $OA = \frac{AC\cdot AD}{DC}=\sqrt{\frac{85}{8}}$, and consequently, the area of the circle is $\pi\cdot OA^2 = \boxed{\textbf{(C) }\frac{85}{8}\pi}$.


Solution 4 (how fast can you multiply two-digit numbers?)

Let $(x,0)$ be the intersection on the x-axis. By Power of a Point Theorem, $(x-6)^2+13^2=(x-12)^2+11^2\implies x=5$. Then the equations for the tangent lines passing $A$ and $B$, respectively, are $13(x-6)+13=y$ and $\frac{11}{7}(x-12)+11=y$. Then the lines normal (perpendicular) to them are $-\frac{1}{13}(x-6)+13=y$ and $-\frac{7}{11}(x-12)+11=y$. Solving for $x$, we have


\[-\frac{7}{11}(x-12)+11=-\frac{1}{13}(x-6)+13\] \[\frac{13\cdot7x-11x}{13\cdot11}=\frac{84\cdot13-6\cdot11-2\cdot11\cdot13}{11\cdot13}\] \[13\cdot7x-11x=84\cdot13-6\cdot11-2\cdot11\cdot13\]

After condensing, $x=\frac{37}{4}$. Then, the center of $\omega$ is $\left(\frac{37}{4}, \frac{51}{4}\right)$. Apply distance formula. WLOG, assume you use $A$. Then, the area of $\omega$ is \[\left(\sqrt{\frac{1^2}{4^2}+\frac{13^2}{4^2}}\right)^2\pi=\frac{170\pi}{16} \implies \boxed{\textbf{(C) }\frac{85}{8}\pi}.\]

Solution 5 (tangent cheese)

After getting $x=5$, let $C=(5,0)$. Get the slopes of the lines $AC$ and $BC$, namely $\frac{13}{6-5}=13$, $\frac{11}{12-5}=\frac{11}{7}$. Then, use tangent angle subtraction to get $\tan{2x}=\frac{13-\frac{11}{7}}{1+13*\frac{11}{7}}=\frac{80}{150}=\frac{8}{15}$. Then, apply tangent double angle to get $\tan{2x}=\frac{8}{15}=\frac{2\tan{x}}{1-\tan^2{x}}$. Solving, we obtain $\tan{x}=\frac{1}{4}$. Then, note that $\tan{x}=r/{BC}$, so $r=\frac{1}{4}*\sqrt{170}$. Finishing off, we obtain $A=\pi*r^2=\pi*170/16=\boxed{\textbf{(C) }\frac{85}{8}\pi}$.

~SigmaPiE

Video Solution

For those who want a video solution: (Is similar to Solution 1) https://youtu.be/WI2NVuIp1Ik

Video Solution by TheBeautyofMath

https://youtu.be/W1zuqrTlBtU

~IceMatrix

Video Solution by The Power of Logic

https://www.youtube.com/watch?v=sQIWSrio_Hc

~The Power of Logic

See Also

2019 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 22 		Followed by
Problem 24
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2019 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2019_AMC_10B_Problems/Problem_23&oldid=207972"