Difference between revisions of "2023 AMC 12B Problems/Problem 25"
(→Solution 2 (In Progress)) |
(→Solution 5 (answer choices (not rigorous))) |
||
| (53 intermediate revisions by 9 users not shown) | |||
| Line 10: | Line 10: | ||
==Solution 1== | ==Solution 1== | ||
| − | [[File:Pentagon_2023_12B_Q25_dissmo.png]] | + | [[File:Pentagon_2023_12B_Q25_dissmo.png|600px]] |
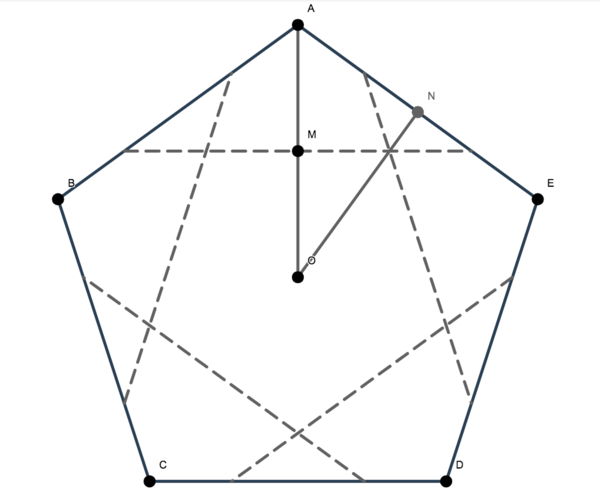
Let the original pentagon be <math>ABCDE</math> centered at <math>O</math>. The dashed lines represent the fold lines. WLOG, let's focus on vertex <math>A</math>. | Let the original pentagon be <math>ABCDE</math> centered at <math>O</math>. The dashed lines represent the fold lines. WLOG, let's focus on vertex <math>A</math>. | ||
| − | Since <math>A</math> is folded onto <math>O</math>, <math> | + | Since <math>A</math> is folded onto <math>O</math>, <math>AM = MO</math> where <math>M</math> is the intersection of <math>AO</math> and the creaseline between <math>A</math> and <math>O</math>. Note that the inner pentagon is regular, and therefore similar to the original pentagon, due to symmetry. |
Because of their similarity, the ratio of the inner pentagon's area to that of the outer pentagon can be represented by | Because of their similarity, the ratio of the inner pentagon's area to that of the outer pentagon can be represented by | ||
| − | <math>(\frac{ | + | <math>\left(\frac{OM}{ON}\right)^{2} = \left(\frac{\frac{OA}{2}}{OA\sin (\angle OAE)}\right)^{2} = \frac{1}{4\sin^{2}54}</math> |
| Line 55: | Line 55: | ||
-Dissmo | -Dissmo | ||
| − | + | ==Solution 2== | |
| − | ==Solution 2 | ||
| Line 215: | Line 214: | ||
</asy> | </asy> | ||
| − | Notice that we have no information about the side length, so instead we let the side length be <math>s</math>. Now we can drop an altitude from <math>O</math> to the base of the triangle, and we know this altitude must split the base of the pentagon in half, so we can create a right triangle. Furthermore, draw a line from <math>O</math> to <math>D</math>. This must bisect angle <math>D</math> which is <math>108</math> degrees, so we create <math>36-54-90</math> triangles. We | + | Notice that we have no information about the side length, so instead we let the side length be <math>s</math>. Now we can drop an altitude from <math>O</math> to the base of the triangle, and we know this altitude must split the base of the pentagon in half, so we can create a right triangle. Furthermore, draw a line from <math>O</math> to <math>D</math>. This must bisect angle <math>D</math> which is <math>108</math> degrees, so we create <math>36-54-90</math> triangles. Specifically, we know <math>\angle ODK = 54^{\circ}</math>, <math>\angle DOU = 36^{\circ}</math>, and <math>\angle DTK = 36^{\circ}</math> because <math>\triangle DTK</math> is isosceles and we know the vertex angle is <math>108^{\circ}</math>. We encode this information in the diagram below: |
| − | |||
<asy> | <asy> | ||
unitsize(5cm); | unitsize(5cm); | ||
| Line 257: | Line 255: | ||
J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); | J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); | ||
| − | label("$F$", | + | label("$F$", (0.1,-1/1.618), E); |
pair K, L, M, N, O, P, Q, R, S, T, U, V; | pair K, L, M, N, O, P, Q, R, S, T, U, V; | ||
| Line 271: | Line 269: | ||
pair U; | pair U; | ||
U=(0,-0.809); | U=(0,-0.809); | ||
| − | label("$U$", | + | label("$U$",(0,-0.9), S); |
draw(O--U); | draw(O--U); | ||
draw(O--D); | draw(O--D); | ||
| + | |||
| + | pair V; | ||
| + | V = midpoint(O--D); | ||
| + | label("$V$", V+(0,0.05), N); | ||
| + | markscalefactor = 0.005; | ||
| + | draw(rightanglemark(D,U,O)); | ||
| + | draw(rightanglemark(F,V,O)); | ||
| + | draw(rightanglemark(K,U,F)); | ||
| + | |||
| + | draw(anglemark(U,D,O)); | ||
| + | |||
| + | label("$54^{\circ}$", D+(0.05,0),NE); | ||
| + | |||
| + | draw(anglemark(D,O,U)); | ||
| + | |||
| + | label("$36^{\circ}$", O-(0,0.2),SW); | ||
| + | |||
| + | draw(anglemark(D,T,F)); | ||
| + | |||
| + | label("$36^{\circ}$", T+(0.1,-0.17),SE); | ||
| + | |||
| + | label("$\frac{s}{2}$", D+(0.3,-0.1), S); | ||
| Line 279: | Line 299: | ||
</asy> | </asy> | ||
| + | Since <math>\triangle DKT</math> is isosceles, the area of <math>\triangle DVT</math> is half the area of <math>\triangle DKT</math>. Similarly, the area of <math>\triangle UFK</math> is half that of <math>\triangle PFK</math>. Thus: | ||
| + | |||
| + | |||
| + | <cmath>[FGHIJ] = [ABCDE]-(5 \cdot[DKT]-5 \cdot [PFK]) \implies [FGHIJ] = [ABCDE]-(10 \cdot [DVT]-10 \cdot [UFK])</cmath> | ||
| + | |||
| + | We also know that since we dropped an altitude from <math>O</math> to <math>U</math>, the area of <math>\triangle ODU</math> must be half of a fifth of the total area of the pentagon. Therefore we can rewrite the above equation as <cmath>[FGHIJ]=10 \cdot ([ODU]-[DVT]+[UFK])</cmath> | ||
| + | |||
| + | Now notice that <math>\triangle ODU ~ \triangle TDV ~ \triangle KFU</math> by AA similarity. Therefore, if we can write the areas of the latter two triangles as a ratio of the first triangle, we can express the whole equation in terms of <math>[ODU]</math>, and by extension <math>[ABCDE]</math>, which we know. To find these ratios, we can find the side length ratios and square them because the triangles are similar. | ||
| + | |||
| + | We already know <math>DU = \frac{s}{2}</math>, so let's try to find it's analogous side for <math>\triangle TDV</math> and <math>\triangle KFU</math>. These sides are <math>DV</math> and <math>FU</math>, respectively. | ||
| + | |||
| + | First, <math>\frac{s}{2} = OD \cdot cos(54^{\circ})</math>, so <math>OD = \frac{s}{2} \cdot sec(54^{\circ})</math>. Then notice that <math>DV = \frac{OD}{2}</math> because we have to fold <math>D</math> to hit <math>O</math>, so the folding crease has to be exactly halfway between <math>O</math> and <math>D</math>. Therefore, <cmath>DV = \frac{s}{4} \cdot sec(54^{\circ}) \implies \frac{DU}{DV} = \frac{\frac{s}{2}}{\frac{s}{4} \cdot sec(54^{\circ})} = 2 \cdot cos(54^{\circ})</cmath> | ||
| + | |||
| + | Now the ratio between the area of two similar triangles is the square of the ratio of their analogous side lengths. Thus | ||
| + | <cmath>\frac{[ODU]}{[TDV]} = 4 \cdot cos^2(54^{\circ}) \implies \frac{10 \cdot [ODU]}{10 \cdot [TDV]} = 4 \cdot cos^2(54^{\circ})</cmath> | ||
| + | <cmath> \implies \frac{[ABCDE]}{10 \cdot [TDV]} = 4 \cdot cos^2(54^{\circ}) \implies \frac{\sqrt{5}+1}{10 \cdot [TDV]} = 4 \cdot cos^2(54^{\circ})</cmath> | ||
| + | <cmath>\implies 10 \cdot [TDV] = \frac{\sqrt{5}+1}{4 \cdot cos^2(54^{\circ})} \implies 10 \cdot [TDV] = \frac{\sqrt{5}+1}{4} \cdot sec^2(54^{\circ})</cmath> | ||
| + | |||
| + | Now let's move on and calculate the ratio of the other side length. Calculating <math>FU</math> is slightly tricker. | ||
| + | First, we find <math>TD</math>: <math>TD \cdot cos(54^{\circ}) = DV = \frac{s}{4} sec^54^{\circ}) \implies TD = \frac{s}{4} \cdot sec^2(54^{\circ})</math>. Now since <math>\triangle DTK</math> is isosceles, <math>TD = DK</math> and <math>UK = DK-DU = TD-DU = \frac{s}{4} \cdot sec^2(54^{\circ})-\frac{s}{2} = \frac{s}{4} \cdot (sec^2(54^{\circ})-2) = \frac{s}{4} \cdot (tan^2(54^{\circ})-1)</math>. | ||
| + | |||
| + | Now <math>FU = UK \cdot tan(36^{\circ}) \implies FU \frac{s}{4} \cdot (tan^2(54^{\circ})-1) \cdot tan(36^{\circ})</math>. Now note that <math>tan(x) \cdot tan(90-x) = 1</math> because opposite over adjacent cancel each other out in a right triangle. Thus, <math>FU = \frac{s}{4} \cdot (tan(54^{\circ})-tan(36^{\circ}))</math> | ||
| + | |||
| + | Now, <cmath>\frac{DU}{FU} = \frac{\frac{s}{2}}{\frac{s}{4} \cdot (tan(54^{\circ})-tan(36^{\circ}))} = \frac{2}{tan(54^{\circ})-tan(36^{\circ})}</cmath> | ||
| + | |||
| + | <cmath>\implies \frac{[DU]}{[FU]} = \frac{4}{(tan(54^{\circ})-tan(36^{\circ}))^2} \implies 10 \cdot [FU] = \frac{1+\sqrt{5}}{4} \cdot (tan(54^{\circ})-tan(36^{\circ}))^2</cmath> | ||
| + | |||
| + | Now we go back to our first equation and plug in our values: | ||
| + | |||
| + | <cmath> [FGHIJ] = [ABCDE]-(10 \cdot [DVT]-10 \cdot [UFK]) \implies [FGHIJ] = 1+\sqrt{5}-\frac{\sqrt{5}+1}{4} \cdot sec^2(54^{\circ})+\frac{1+\sqrt{5}}{4} \cdot (tan(54^{\circ})-tan(36^{\circ}))^2</cmath> | ||
| + | |||
| + | <cmath>\implies [FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (4-sec^2(54^{\circ})+(tan(54^{\circ})-tan(36^{\circ}))^2)</cmath> | ||
| + | |||
| + | Note <math>(tan(x)-tan(90-x))^2 = tan^2(x)-2 \cdot tan(x) \cdot tan(90-x)+tan^2(90-x) = tan^2(x)-2+tan^2(90-x)</math>. | ||
| + | Also note that <math>tan^2(x)+1 = sec^2(x)</math>. | ||
| + | Thus <cmath>[FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (2-sec^2(54^{\circ})+tan^2(54^{\circ})+tan^2(36^{\circ}))</cmath> | ||
| + | <cmath>\implies [FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (2+(-1)+tan^2(36^{\circ})) \implies [FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (1+tan^2(36^{\circ}))</cmath>. | ||
| + | Now all that remains is to find <math>tan^2(36^{\circ})</math>. We can use the tan addition formula to find the general form of <math>tan(5x)</math> or remember question 25 from this year's AMC 12A. We have that <cmath>tan(5x) = \frac{5tan(x)-10tan^3(x)+tan^5(x)}{1-10tan^2(x)+5tan^4(x)}</cmath>. | ||
| + | Plug in <math>x=36</math>. Then we have <cmath>tan(180^{\circ}) = \frac{5tan(36^{\circ})-10tan^3(36^{\circ})+tan^5(36^{\circ})}{1-10tan^2(36^{\circ})+5tan^4(36^{\circ})}</cmath> | ||
| + | Now let <math>y = tan(36^{\circ})</math>. We have the equation <cmath>\frac{5y-10y^3+y^5}{1-10y^2+5y^4} = 0 \implies 5y-10y^3+y^5 = 0</cmath> | ||
| + | <cmath>\implies 5-10y^2+y^4 = 0 \implies 5-10z+z^2 = 0</cmath> | ||
| + | Where we let <math>z = y^2</math>. Using the quadratic formula, we have <cmath>z = \frac{10 \pm \sqrt{80}}{2} = 5 \pm 2\sqrt{5}</cmath> | ||
| + | Now since <math>y = tan(36^{\circ})</math>, <math>z = tan^2(36^{\circ})</math>, which is what we were looking for. Notice that <math>tan(0^{\circ}) = 0</math> and <math>tan(45^{\circ}) = 1</math>, so <math>tan(36^{\circ})</math> is between <math>0</math> and <math>1</math>, and so is it's square. Thus <math>z = 5 - 2\sqrt{5}</math>, not the other root. | ||
| + | Finally: | ||
| + | <cmath>[FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (1+tan^2(36^{\circ})) = \frac{1+\sqrt{5}}{4} \cdot (1+5-2\sqrt{5})</cmath> | ||
| + | <cmath>\implies [FGHIJ] = \frac{1+\sqrt{5}}{4} \cdot (6-2\sqrt{5}) = \frac{4\sqrt{5}-4}{4} = \sqrt{5}-1</cmath> | ||
| + | |||
| + | Therefore, <cmath>[FGHIJ] = \sqrt{5}-1 = \boxed{B}</cmath> | ||
~KingRavi | ~KingRavi | ||
| − | ==Solution | + | ==Solution 3== |
<asy> | <asy> | ||
| Line 354: | Line 422: | ||
A_s &= \left(\dfrac{r_s}{r_b}\right)^2A_b\\ | A_s &= \left(\dfrac{r_s}{r_b}\right)^2A_b\\ | ||
&=\left(\dfrac{a_s}{\cos{36^\circ} r_b}\right)^2 \left(1+\sqrt{5}\right)\\ | &=\left(\dfrac{a_s}{\cos{36^\circ} r_b}\right)^2 \left(1+\sqrt{5}\right)\\ | ||
| − | &=\left(\dfrac{ | + | &=\left(\dfrac{a_s}{\dfrac{\phi}{2} r_b}\right)^2 \left(1+\sqrt{5}\right)\\ |
&=\left(\dfrac{1}{2 \dfrac{\phi}{2}}\right)^2 \left(1+\sqrt{5}\right)\\ | &=\left(\dfrac{1}{2 \dfrac{\phi}{2}}\right)^2 \left(1+\sqrt{5}\right)\\ | ||
&=\left(\dfrac{2}{\sqrt{5}+1}\right)^2 \left(1+\sqrt{5}\right)\\ | &=\left(\dfrac{2}{\sqrt{5}+1}\right)^2 \left(1+\sqrt{5}\right)\\ | ||
| Line 364: | Line 432: | ||
~Technodoggo | ~Technodoggo | ||
| − | ==Solution | + | ==Solution 4== |
Interestingly, we find that the pentagon we need is the one that is represented by the intersection of perpendicular bisectors of the connection from the center of the pentagon to one vertex. Through similar triangles and the golden ratio, we find that the side length ratio of the two pentagons is <math>\frac{\sqrt{5}-1}{2}</math> Thus, the answer is <math>\sqrt{5}+1 \cdot (\frac{\sqrt{5}-1}{2})^2 = \sqrt{5}-1</math>. <math>\boxed{\text{B}}</math> | Interestingly, we find that the pentagon we need is the one that is represented by the intersection of perpendicular bisectors of the connection from the center of the pentagon to one vertex. Through similar triangles and the golden ratio, we find that the side length ratio of the two pentagons is <math>\frac{\sqrt{5}-1}{2}</math> Thus, the answer is <math>\sqrt{5}+1 \cdot (\frac{\sqrt{5}-1}{2})^2 = \sqrt{5}-1</math>. <math>\boxed{\text{B}}</math> | ||
~andliu766 | ~andliu766 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Supplement (Calculating sin54/cos36 from Scratch)== | ==Supplement (Calculating sin54/cos36 from Scratch)== | ||
| Line 395: | Line 442: | ||
[[File:2023AMC12BP25.png|center|250px]] | [[File:2023AMC12BP25.png|center|250px]] | ||
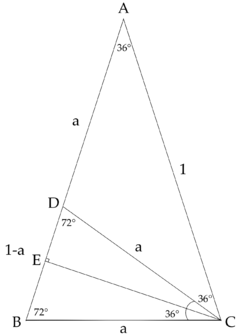
| − | Construct golden ratio triangle <math>\triangle ABC</math> with <math>\angle A = 36^{\circ}</math>, <math>\angle B = \angle C = 72^{\circ}</math> and <math>\triangle BCD</math> with <math>\angle C = 36^{\circ}</math>, <math>\angle DBC = \angle BDC = 72^{\circ}</math>. WLOG, let <math>AB = AC = 1</math>, <math>BC = CD = AD = a</math>, <math>BD = 1-a</math>. <math>\triangle | + | Construct golden ratio triangle <math>\triangle ABC</math> with <math>\angle A = 36^{\circ}</math>, <math>\angle B = \angle C = 72^{\circ}</math> and <math>\triangle BCD</math> with <math>\angle C = 36^{\circ}</math>, <math>\angle DBC = \angle BDC = 72^{\circ}</math>. WLOG, let <math>AB = AC = 1</math>, <math>BC = CD = AD = a</math>, <math>BD = 1-a</math>. <math>\triangle BAC \sim \triangle BCD</math> |
<cmath>\frac{AC}{BC} = \frac{BC}{BD}, \quad \frac{1}{a} = \frac{a}{1-a}, \quad 1-a=a^2, \quad a^2 + a - 1 = 0</cmath> | <cmath>\frac{AC}{BC} = \frac{BC}{BD}, \quad \frac{1}{a} = \frac{a}{1-a}, \quad 1-a=a^2, \quad a^2 + a - 1 = 0</cmath> | ||
| Line 401: | Line 448: | ||
<cmath>a = \frac{ -1 + \sqrt{1^2 - 4(-1) } }{2} = \frac{ \sqrt{5} -1 }{2}</cmath> | <cmath>a = \frac{ -1 + \sqrt{1^2 - 4(-1) } }{2} = \frac{ \sqrt{5} -1 }{2}</cmath> | ||
| − | <cmath>\cos 36^{\circ} = \cos \angle A = \frac{AE}{AC} = \frac{ 1-a }{2} + | + | <cmath>\cos 36^{\circ} = \cos \angle A = \frac{AE}{AC} = \frac{ 1-a }{2} + a = \frac{ a + 1 }{2} = \frac{ \frac{ \sqrt{5} -1 }{2} + 1 }{2} = \frac{ \sqrt{5} + 1 }{4}</cmath> |
<cmath>\sin 54^{\circ} = \cos 36^{\circ} = \frac{ \sqrt{5} + 1 }{4}</cmath> | <cmath>\sin 54^{\circ} = \cos 36^{\circ} = \frac{ \sqrt{5} + 1 }{4}</cmath> | ||
| Line 434: | Line 481: | ||
{{AMC10 box|year=2023|ab=B|num-b=24|after=Last Problem}} | {{AMC10 box|year=2023|ab=B|num-b=24|after=Last Problem}} | ||
{{AMC12 box|year=2023|ab=B|num-b=24|after=Last Problem}} | {{AMC12 box|year=2023|ab=B|num-b=24|after=Last Problem}} | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 18:17, 15 August 2024
- The following problem is from both the 2023 AMC 10B #25 and 2023 AMC 12B #25, so both problems redirect to this page.
Contents
Problem
A regular pentagon with area ![]() is printed on paper and cut out. The five vertices of the pentagon are folded into the center of the pentagon, creating a smaller pentagon. What is the area of the new pentagon?
is printed on paper and cut out. The five vertices of the pentagon are folded into the center of the pentagon, creating a smaller pentagon. What is the area of the new pentagon?
![]()
Solution 1
Let the original pentagon be ![]() centered at
centered at ![]() . The dashed lines represent the fold lines. WLOG, let's focus on vertex
. The dashed lines represent the fold lines. WLOG, let's focus on vertex ![]() .
.
Since ![]() is folded onto
is folded onto ![]() ,
, ![]() where
where ![]() is the intersection of
is the intersection of ![]() and the creaseline between
and the creaseline between ![]() and
and ![]() . Note that the inner pentagon is regular, and therefore similar to the original pentagon, due to symmetry.
. Note that the inner pentagon is regular, and therefore similar to the original pentagon, due to symmetry.
Because of their similarity, the ratio of the inner pentagon's area to that of the outer pentagon can be represented by

Option 1: Knowledge
Remember that ![]() .
.
Option 2: Angle Identities
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Let the inner pentagon be ![]() .
.
![]()
![]()
![]()
![]()
-Dissmo
Solution 2
![[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); // Draw the larger pentagon draw(A--B--C--D--E--cycle); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); label("$O$", O, S); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); dot(O); label("$A$", (0,1), E); label("$B$", B, S); label("$C$", C, S); label("$D$", D, S); label("$E$", E, W); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); pair K, L, M, N, O, P, Q, R, S, T, U, V; real newScaleFactor = 0.8507; K = newScaleFactor*dir(270+18); L = newScaleFactor*dir(270+72+18); M = newScaleFactor*dir(270+72+72+18); N = newScaleFactor*dir(270+72+72+72+18); O = newScaleFactor*dir(270+72+72+72+72+18); P = newScaleFactor*dir(270-18); Q = newScaleFactor*dir(270+72-18); R = newScaleFactor*dir(270+72+72-18); S = newScaleFactor*dir(270+72+72+72-18); T = newScaleFactor*dir(270+72+72+72+72-18); label("$K$", K, S); label("$L$", L, S); label("$M$", M, S); label("$N$", N, S); label("$O$", O, W); label("$P$", P, S); label("$Q$", Q, E); label("$R$", R, S); label("$S$", S, S); label("$T$", T, W); draw(K--T, dashed); draw(S--O, dashed); draw(P--L, dashed); draw(Q--M, dashed); draw(R--N, dashed); label("$F$", F, S); label("$G$", G, S); label("$H$", H, S); label("$I$", I, S); label("$J$", J, S); // Draw the smaller pentagon draw(F--G--H--I--J--cycle,red); [/asy]](http://latex.artofproblemsolving.com/a/3/9/a39d57ed04eca3718be7c068676345ada45cd8a3.png)
We can find the area of the red pentagon by taking the area of the total pentagon and subtracting the area outside the red pentagon.
The area outside the red pentagon is the sum of the larger isosceles triangles, but this double counts the overlapping regions of the small isosceles triangles, so we have to subtract those out.
We have ![]()
Lets focus on finding the area of each individual triangle:
![[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); label("$O$", O, S); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); dot(O); label("$D$", D, S); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); label("$F$", F, N); pair K, L, M, N, O, P, Q, R, S, T, U, V; real newScaleFactor = 0.8507; K = newScaleFactor*dir(270+18); T = newScaleFactor*dir(270+72+72+72+72-18); label("$K$", K, E); label("$T$", T, W); draw(K--T); draw(K--D); draw(D--T); [/asy]](http://latex.artofproblemsolving.com/c/d/a/cda5c862c04e101c0a00068a7a0c1cfe5f75a30e.png)
Notice that we have no information about the side length, so instead we let the side length be ![]() . Now we can drop an altitude from
. Now we can drop an altitude from ![]() to the base of the triangle, and we know this altitude must split the base of the pentagon in half, so we can create a right triangle. Furthermore, draw a line from
to the base of the triangle, and we know this altitude must split the base of the pentagon in half, so we can create a right triangle. Furthermore, draw a line from ![]() to
to ![]() . This must bisect angle
. This must bisect angle ![]() which is
which is ![]() degrees, so we create
degrees, so we create ![]() triangles. Specifically, we know
triangles. Specifically, we know ![]() ,
, ![]() , and
, and ![]() because
because ![]() is isosceles and we know the vertex angle is
is isosceles and we know the vertex angle is ![]() . We encode this information in the diagram below:
. We encode this information in the diagram below:
![[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); label("$O$", O, E); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); dot(O); label("$D$", D, S); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); label("$F$", (0.1,-1/1.618), E); pair K, L, M, N, O, P, Q, R, S, T, U, V; real newScaleFactor = 0.8507; K = newScaleFactor*dir(270+18); T = newScaleFactor*dir(270+72+72+72+72-18); label("$K$", K, S); label("$T$", T, W); draw(K--T); draw(K--D); draw(D--T); pair U; U=(0,-0.809); label("$U$",(0,-0.9), S); draw(O--U); draw(O--D); pair V; V = midpoint(O--D); label("$V$", V+(0,0.05), N); markscalefactor = 0.005; draw(rightanglemark(D,U,O)); draw(rightanglemark(F,V,O)); draw(rightanglemark(K,U,F)); draw(anglemark(U,D,O)); label("$54^{\circ}$", D+(0.05,0),NE); draw(anglemark(D,O,U)); label("$36^{\circ}$", O-(0,0.2),SW); draw(anglemark(D,T,F)); label("$36^{\circ}$", T+(0.1,-0.17),SE); label("$\frac{s}{2}$", D+(0.3,-0.1), S); [/asy]](http://latex.artofproblemsolving.com/c/8/9/c89d27c7817173e8d75a98060a7d819b80331ccb.png)
Since ![]() is isosceles, the area of
is isosceles, the area of ![]() is half the area of
is half the area of ![]() . Similarly, the area of
. Similarly, the area of ![]() is half that of
is half that of ![]() . Thus:
. Thus:
![]()
We also know that since we dropped an altitude from ![]() to
to ![]() , the area of
, the area of ![]() must be half of a fifth of the total area of the pentagon. Therefore we can rewrite the above equation as
must be half of a fifth of the total area of the pentagon. Therefore we can rewrite the above equation as ![]()
Now notice that ![]() by AA similarity. Therefore, if we can write the areas of the latter two triangles as a ratio of the first triangle, we can express the whole equation in terms of
by AA similarity. Therefore, if we can write the areas of the latter two triangles as a ratio of the first triangle, we can express the whole equation in terms of ![]() , and by extension
, and by extension ![]() , which we know. To find these ratios, we can find the side length ratios and square them because the triangles are similar.
, which we know. To find these ratios, we can find the side length ratios and square them because the triangles are similar.
We already know ![]() , so let's try to find it's analogous side for
, so let's try to find it's analogous side for ![]() and
and ![]() . These sides are
. These sides are ![]() and
and ![]() , respectively.
, respectively.
First, ![]() , so
, so ![]() . Then notice that
. Then notice that ![]() because we have to fold
because we have to fold ![]() to hit
to hit ![]() , so the folding crease has to be exactly halfway between
, so the folding crease has to be exactly halfway between ![]() and
and ![]() . Therefore,
. Therefore, ![]()
Now the ratio between the area of two similar triangles is the square of the ratio of their analogous side lengths. Thus
![]()
![]()
![]()
Now let's move on and calculate the ratio of the other side length. Calculating ![]() is slightly tricker.
First, we find
is slightly tricker.
First, we find ![]() :
: ![]() . Now since
. Now since ![]() is isosceles,
is isosceles, ![]() and
and ![]() .
.
Now ![]() . Now note that
. Now note that ![]() because opposite over adjacent cancel each other out in a right triangle. Thus,
because opposite over adjacent cancel each other out in a right triangle. Thus, ![]()
Now, ![]()
![]()
Now we go back to our first equation and plug in our values:
![]()
![]()
Note ![]() .
.
Also note that ![]() .
Thus
.
Thus ![]()
![]() .
.
Now all that remains is to find ![]() . We can use the tan addition formula to find the general form of
. We can use the tan addition formula to find the general form of ![]() or remember question 25 from this year's AMC 12A. We have that
or remember question 25 from this year's AMC 12A. We have that ![]() .
.
Plug in ![]() . Then we have
. Then we have ![]() Now let
Now let ![]() . We have the equation
. We have the equation ![]()
![]() Where we let
Where we let ![]() . Using the quadratic formula, we have
. Using the quadratic formula, we have ![]() Now since
Now since ![]() ,
, ![]() , which is what we were looking for. Notice that
, which is what we were looking for. Notice that ![]() and
and ![]() , so
, so ![]() is between
is between ![]() and
and ![]() , and so is it's square. Thus
, and so is it's square. Thus ![]() , not the other root.
, not the other root.
Finally:
![]()
![]()
Therefore, ![]()
~KingRavi
Solution 3
![[asy] unitsize(5cm); // Define the vertices of the pentagons pair A, B, C, D, E; pair F, G, H, I, J; // Calculate the vertices of the larger pentagon A = dir(90); B = dir(90 - 72); C = dir(90 - 2*72); D = dir(90 - 3*72); E = dir(90 - 4*72); // Draw the larger pentagon draw(A--B--C--D--E--cycle); pair O = (A+B+C+D+E)/5; pair AA,OO; real gap = 0.02; AA = A+(0,0); OO = O+(0,0); draw(AA--OO, blue); pair OOO, OAO; OOO = O+(gap,0); OAO = (O+A)/2 + (gap,0); draw(OOO--OAO,green); dot(O); dot((O+A)/2); label("$r_b$", (O+A)*.7, E,blue); label("$a_s$", (O+A)*.2 +(0+0.18,0.05), E,green); label("$r_s$", O+(-0.175,0.2), E,pink); label("$A$", (0,0), E); real scaleFactor = 1/1.618; // Adjust this value as needed // Rotate the smaller pentagon by 180 degrees F = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 + 180); G = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 72 + 180); H = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 2*72 + 180); I = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 3*72 + 180); J = (1 - scaleFactor) * (0,0) + scaleFactor * dir(90 - 4*72 + 180); // Draw the smaller pentagon draw(F--G--H--I--J--cycle,red); draw(arc(O,(H+I)*.5*.6,H*.6)); label("$36^\circ$",O+(+0.05,0.15),NW); draw(O--H,pink); [/asy]](http://latex.artofproblemsolving.com/2/e/c/2ec47e2f32e2670699129d125c4ed651625a0ac6.png)
Let ![]() and
and ![]() be the circumradius of the big and small pentagon, respectively. Let
be the circumradius of the big and small pentagon, respectively. Let ![]() be the apothem of the smaller pentagon and
be the apothem of the smaller pentagon and ![]() and
and ![]() be the areas of the smaller and larger pentagon, respectively.
be the areas of the smaller and larger pentagon, respectively.
From the diagram:

![]() ~Technodoggo
~Technodoggo
Solution 4
Interestingly, we find that the pentagon we need is the one that is represented by the intersection of perpendicular bisectors of the connection from the center of the pentagon to one vertex. Through similar triangles and the golden ratio, we find that the side length ratio of the two pentagons is ![]() Thus, the answer is
Thus, the answer is ![]() .
. ![]() ~andliu766
~andliu766
Supplement (Calculating sin54/cos36 from Scratch)
Method 1:
Construct golden ratio triangle ![]() with
with ![]() ,
, ![]() and
and ![]() with
with ![]() ,
, ![]() . WLOG, let
. WLOG, let ![]() ,
, ![]() ,
, ![]() .
. ![]()
![]()
![]()
![]()
![]()
Method 2:
As explained here, ![]()
![]()
![]()
![]()
![]()
Video Solution 1 by SpreadTheMathLove
https://www.youtube.com/watch?v=ROVjN3oYLbQ
Video Solution 2 by OmegaLearn
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
See also
| 2023 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2023 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.