Difference between revisions of "2005 AIME I Problems/Problem 11"

Revision as of 00:22, 2 March 2008

Problem

A semicircle with diameter $d$ is contained in a square whose sides have length 8. Given the maximum value of $d$ is $m - \sqrt{n},$ find $m+n.$

Solution

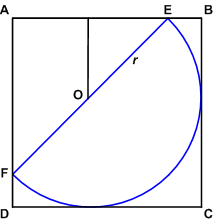
We note that aligning the base of the semicircle with a side of the square is certainly non-optimal. If the semicircle is tangent to only one side of the square, we will have "wiggle-room" to increase its size. Once it is tangent to two adjacent sides of the square, we will maximize its size when it touches both other sides of the square. This can happen only when it is arranged so that the center of the semicircle lies on one diagonal of the square.

Now, let the square be $ABCD$ , and let $E \in AB$ and $F \in DA$ be the points at which the "corners" of the semicircle touch the square. Let $O$ be the center of the semicircle.

Solution 1

Define the radius of the semicircle as $r$ . Draw the perpendicular from $O$ to $AB$ , which forms a $45-45-90$ triangle. The length of the perpendicular is $\frac{r}{\sqrt{2}}$ . Note also that $AD$ is equal to the length of that perpendicular plus the radius to the point of tangency on $CD$ . Thus, $r + \frac{r}{\sqrt{2}} = 8$ , and $r = \frac{8\sqrt{2}}{\sqrt{2} + 1} \cdot (\frac{\sqrt{2} - 1}{\sqrt{2} - 1}) = 16 - 8\sqrt{2}$ . The diameter is then $2r = 32 - \sqrt{512}$ , and the solution is $32 + 512 = 544$ .

Solution 2

By the comments above, $AE = AF = a$ . By the Pythagorean Theorem, $d^2 = 2a^2$ .

Now, if we draw a line through the center, $O$ , of the semicircle and its point of tangency with $BC$ , we see that this line is perpendicular to $BC$ and so parallel to $AB$ . Thus, by triangle similarity it cuts $AF$ in half, and so by symmetry the distance from $O$ to $AD$ is $\frac{a}{2}$ and so the distance from $O$ to $BC$ is $8 - \frac a2$ . But this latter quantity is also the radius of the semicircle, so $d = 16 - a$ .

Our two previous paragraphs give $2a^2 = (16 - a)^2$ so $a^2 + 32a - 256 = 0$ and $a = 16\sqrt{2} - 16$ (where we discard the negative root of that quadratic) and so $d = a\sqrt{2} = 32 - 16\sqrt{2} = 32 - \sqrt{512}$ , so the answer is $32 + 512 = 544$ .

@@ Line 20: / Line 20: @@
 Our two previous paragraphs give <math>2a^2 = (16 - a)^2</math> so <math>a^2 + 32a - 256 = 0</math> and <math>a = 16\sqrt{2} - 16</math> (where we discard the negative root of that quadratic) and so <math>d = a\sqrt{2} = 32 - 16\sqrt{2} = 32 - \sqrt{512}</math>, so the answer is <math>32 + 512 = 544</math>.
-== Solution 3 ==
-Call the point of tangency from <math>O</math> to <math>BC</math> <math>N</math>. Let the extensions of <math>BC</math> and <math>OE</math> intersect at <math>M</math>. <math>ON=r</math>, and because triangle <math>ONM</math> is iscosceles and right, <math>OM=r\sqrt{2}</math>. But <math>NC=r</math>, so <math>BN=8-r</math> and <math>BM=r-(8-r)=2r-8</math>, so <math>EM=\sqrt{2}(2r-8)</math>. Since <math>OE+EM=OM</math>, we have <math>r+\sqrt{2}(2r-8)=r\sqrt{2}</math>. Solving gives the diameter=<math>32-\sqrt{512}</math>, so the answer is <math>544</math>.
 == See also ==

2005 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 10	Followed by Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search